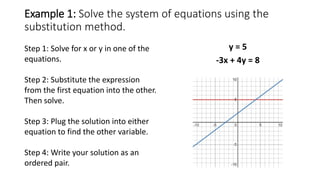
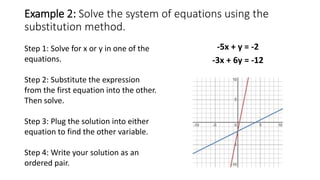
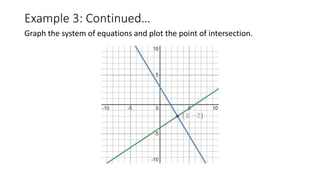
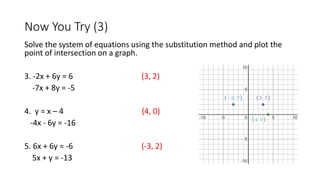
The document describes the substitution method for solving systems of linear equations. It provides examples of using the substitution method to solve systems of two equations with two unknowns. The steps are: (1) solve one equation for one variable, (2) substitute this expression into the other equation and solve, (3) substitute the solution back to find the other variable, (4) write the solution as an ordered pair. Video clips demonstrate the method and examples provide the full working of the substitution method to find the point of intersection for systems of equations. Practice problems are given for readers to try applying the substitution method on their own.

1. The Substitution Method
Unit topic: Solving Systems of Equations
Class: Algebra (Grade 9)
By Alberto Preciado

2. Lecture objectives:
• Solve systems of linear equations exactly and approximately
• Determine which type of systems can be solved using
substitution
• Find the point of intersection
• Graph the system of equations

3. 3 Methods to Solving Systems of Equations
1. Substitution
2. Elimination
3. Graphing

4. The Substitution Method
• The substitution method is a simple way to solve linear
equations algebraically and find the solutions of the
variables.
• The substitution method requires solving for one variable,
and then substituting that expression into the second
equation.

5. Example 1: Solve the system of equations using the
substitution method.
y = 5
-3x + 4y = 8
Step 1: Solve for x or y in one of the
equations.
Step 2: Substitute the expression
from the first equation into the other.
Then solve.
Step 3: Plug the solution into either
equation to find the other variable.
Step 4: Write your solution as an
ordered pair.

6. Example 1: Continued…
Step 1.
y = 5
-3x + 4y = 8
Step 2.
-3x + 4(5) = 8
-3x + 20 = 8
-3x = -12
x = 4
Step 3.
-3(4) + 4y = 8
-12 + 4y = 8
4y = 20
y = 5
Step 4.
(x, y) = (4, 5)

7. Video Clips
Please watch these step-by-step videos on how to solve a system of
equations using the substitution method.

8. Now You Try (1)
Solve the system of equations using the substitution method.
1. y = 5x − 7
−3x − 2y = −12

9. Now You Try (1)
Solve the system of equations using the substitution method.
1. y = 5x − 7 (2, 3)
−3x − 2y = −12

10. Example 2: Solve the system of equations using the
substitution method.
-5x + y = -2
-3x + 6y = -12
Step 1: Solve for x or y in one of the
equations.
Step 2: Substitute the expression
from the first equation into the other.
Then solve.
Step 3: Plug the solution into either
equation to find the other variable.
Step 4: Write your solution as an
ordered pair.

11. Example 2: Continued…
Step 1.
-5x + y = -2
-3x + 6y = -12
y = -2 + 5x
-3x + 6y = -12
Step 2.
-3x + 6(-2 + 5x) = -12
-3x -12 + 30x = -12
27x = 0
x = 0
Step 3.
y = -2 + 5(0)
y = -2
-3(0) + 6y = -12
6y = -12
y = -2
Step 4.
(x, y) = (0, -2)

12. Now You Try (2)
Solve the system of equations using the substitution method.
2. x + 3y = 1
−3x − 3y = −15

13. Now You Try (2)
Solve the system of equations using the substitution method.
2. x + 3y = 1 (7, -2)
−3x − 3y = −15

14. Example 3: For each question, solve the system of equations
by substitution and plot the point of intersection on the
graph.
5x + 3y = 9
2x − 3y = 12
Step 1: Solve for x or y in one of the
equations.
Step 2: Substitute the expression
from the first equation into the other.
Then solve.
Step 3: Plug the solution into either
equation to find the other variable.
Step 4: Write your solution as an
ordered pair.

15. Example 3: Continued…
Step 1.
5x + 3y = 9
2x − 3y = 12
5x + 3y = 9
x = (3/2)y + 6
Step 2.
5((3/2)y = 6) + 3y = 9
(15/2)y + 30 + 3y = 9
(21/2)y = -21
y = -2
Step 3.
5x + 3(-2) = 9
5x = 15
x = 3
2x - 3(-2) = 12
2x = 6
x = 3
Step 4.
(x, y) = (3, -2)

16. Example 3: Continued…
Graph the system of equations and plot the point of intersection.

17. Now You Try (3)
Solve the system of equations using the substitution method and plot the
point of intersection on a graph.
3. -2x + 6y = 6 (3, 2)
-7x + 8y = -5
4. y = x – 4 (4, 0)
-4x - 6y = -16
5. 6x + 6y = -6 (-3, 2)
5x + y = -13