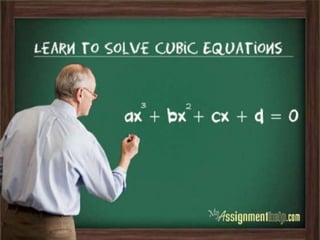This document provides a comprehensive guide to solving cubic equations, emphasizing that they always have at least one real root and can typically be reduced to quadratic equations for solution. It details the use of the factor theorem and synthetic division as methods to find the roots of cubic equations, providing examples and step-by-step instructions. Additionally, it promotes a writing service, myassignmenthelp.com, for students seeking assistance with mathematics assignments.

1. Introduction
Learn to Solve Cubic Equations
In mathematical terms, all cubic equations have
either one root or three real roots. The general
cubic equation is,
ax3+ bx2+ cx+d= 0
The coefficients of a, b, c and d are real or
complex numbers with a not equals to zero
(a ≠ 0). It must have the term x3 in it, or else it
will not be a cubic equation.

2. Introduction
The coefficients of a, b, c and d are real or
complex numbers with a not equals to zero
(a ≠ 0). It must have the term x3 in it, or else it
will not be a cubic equation. But any or all of b, c
and d can be zero.
The examples of cubic equations are,
No 1, x3+ 3a3+ 3 a2 + a3– b=0
No 2, 4x3+ 57=0
No 3, x3+ 9x=0

4. Strategy to Solve Cubic
Equation
Unlike quadratic equation which may have no
real solution; a cubic equation always has at
least one real root. The prior strategy of solving
a cubic equation is to reduce it to a quadratic
equation, and then solve the quadratic by usual
means, either by factorizing or using a formula.
Always try to find the solution of cubic
equations with the help of the general equation,
ax3+ bx2+ cx+d= 0

5. Strategy to Solve Cubic
Equation
A cubic equation should, therefore, must be re-
arranged into its standard form,
For example,
x2+ 4x-1 = 6/x

6. Strategy to Solve Cubic
Equation
Step 1
You can see the equation is not written in
standard form, you need to multiply the ‘x’ to
eliminate the fraction and get cubic equation,
after doing so, you will end up with
x3+ 4x2– x = 6

7. Strategy to Solve Cubic
Equation
Step 2
Then you subtract 6 from both sides in order to
get ‘0’ on the right side, so you will come up,
x3+ 4x2– x- 6 = 0

8. Solving Cubic Equations with
the help of Factor Theorem
What is factor theorem? If you divide a
polynomial p(x) by a factor x – a of that
polynomial, then, you will end up with zero as
the remainder,
p(x) = (x – a)q(x) + r(x)

9. Solving Cubic Equations with
the help of Factor Theorem
If x – a is indeed a factor of p(x), then the
remainder after division by x – a will be zero.
p(x) = (x – a)q (x)
Here is a problem,
x3– 5x2– 2x+24 = 0
With x= – 2 a solution.

10. Solving Cubic Equations with
the help of Factor Theorem
If x – a is indeed a factor of p(x), then the
remainder after division by x – a will be zero.
p(x) = (x – a)q (x)
Here is a problem,
x3– 5x2– 2x+24 = 0
With x= – 2 a solution.

11. Solving Cubic Equations with
the help of Factor Theorem
Factor theorem says that if x = – 2 is a solution
of this equation, then x+2 is a factor of this
whole expression.

12. Solving Cubic Equations with
the help of Factor Theorem
Step 1
First, you need to look at the coefficients of the
original cubic equation, which are 1, -5, -
2 and 24.

13. Solving Cubic Equations with
the help of Factor Theorem
Step 2
Now multiply number (1) that just brought
down, by the known root -2, as a result is -2, you
mention the result in the other line, like

14. Solving Cubic Equations with
the help of Factor Theorem
Step 3
The numbers in the second column are added,
so giving us,

15. Solving Cubic Equations with
the help of Factor Theorem
Step 4
Then recently written number 7 is multiplied by
the known root, – 2,
As 14 comes as a result, you need to write it
down on the second row over the line,

16. Solving Cubic Equations with
the help of Factor Theorem
Step 5
Like previously the numbers in this column
added, (14 – 2 = 12)

17. Solving Cubic Equations with
the help of Factor Theorem
Step 6
And you need to go on with the process,

18. Solving Cubic Equations with
the help of Factor Theorem
Step 7
When you have zero at the bottom row, it gives
the confirmation that x = – 2 is a root of the
original cubic. At this stage, you got the first
three numbers in the bottom row as the
coefficients in the quadratic,
x2– 7x+12
Hence, you reduced your cubic to,

19. Solving Cubic Equations with
the help of Factor Theorem
(x+2)(x2 – 7x + 12) =0
Step 8
After applying the quadratic term, the equation
comes like this,
(x +2) (x – 3) (x – 4) = 0
Resulting, you get the solution as x = -2 or 3 or 4.

20. Solving Cubic Equations with
the help of Factor Theorem
Another Example:
The equation is,
x3– 7x-6=0
Step 1 You can simply try x = – 1, after putting
the value of x, you will get,
(-1)3 – 7(-1) -6

21. Solving Cubic Equations with
the help of Factor Theorem
Step 2
After applying the synthetic division, like above
example, you will take the coefficients of the
original cubic equation, which are 1, 0, -7 and -6,
you need to write down the know root x = -1 to
the right of the vertical line, giving us,

22. Solving Cubic Equations with
the help of Factor Theorem
Step 3
Multiply the brought down number 1 by the
known root x = -1, and put down the result (-
1) at the second row, like this,

23. Solving Cubic Equations with
the help of Factor Theorem
Step 4
The numbers of the second column are added to
the first column, giving us,

24. Solving Cubic Equations with
the help of Factor Theorem
Step 5
As you add more numbers to the second column
by following the synthetic division process, you
will come with,

25. Solving Cubic Equations with
the help of Factor Theorem
Step 6
Hence, the cubic reduced to quadratic,
(x+1)(x2-x- 6) =0
The factorized result is,
(x +1)(x – 3)(x + 2) = 0
You can get three solutions to the cubic
equation are x = -2, -1 or 3

26. Are you looking for Assignment
Help with 100% accuracy,
My assignment help .com have
3000+ Professional Writers are
here to help with your
Assignment Writing & also
provide 24×7 Online Support.

27. How MyAssignmenthelp.com can help students
in maths assignment?
MyAssignmenthelp.com has carefully evaluated and
assembled a highly-skilled team of in-house experts
who are capable of giving the finest maths homework
help you deserve. Your paper will be written by
experienced writers in a professional
manner. Assignment experts make sure that there are
no traces of plagiarism in your content, they only deliver
genuine work within the given time limit. If you think
sample assignments can help you in your assignment,
MyAssignmenthelp.com offers free samples. Our
customer support agents can guide you on how to get
free assignments quotes and place your orders.

28. Australia
+61-3-4000-0033
Dubai
+971-8000320360
United Kingdom
+44-121-285-4112
Mail Id
contact@myassignmenthelp.com
Contact Us