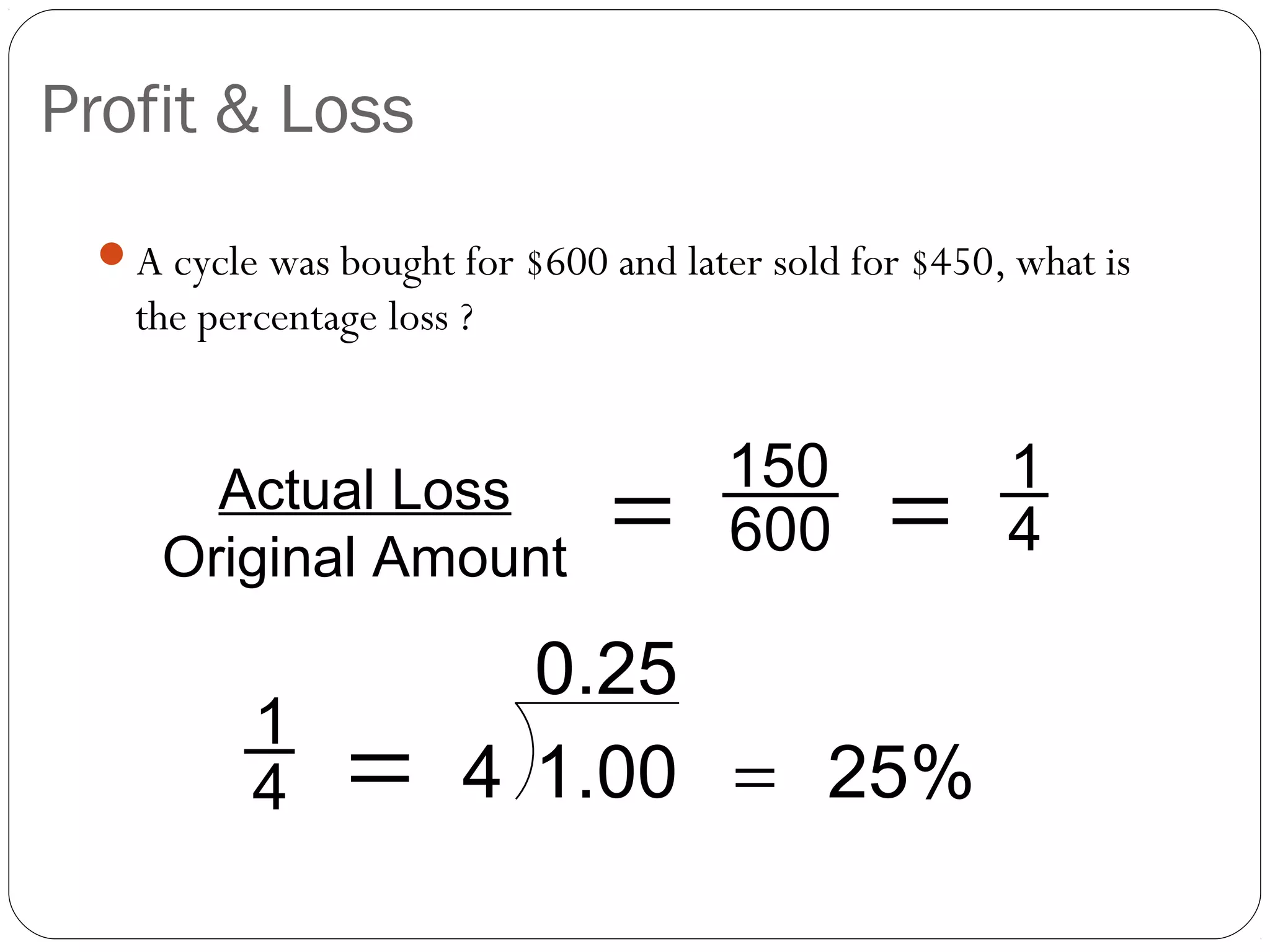This document provides information and examples for working with percentages and discounts. It covers converting between fractions, decimals, and percentages; finding percentages of quantities; calculating profit and loss; reversing percentages to find original values; and writing quantities as percentages of others. Examples are provided for each topic without and with a calculator. The next session will cover working with ratios.

1. YEAR 8 ECHO MATHEMATICS
Percentages and
Discounts
1

2. Contents
Converting between Fractions Decimals and Percentages
Finding a Percentage
Profit & Loss
Reverse Percentages
 Writing as a Percentage
2 14/03/13

3. Converting between F, D & P
Converting a percentage to a fraction
40% means 40 out of every 100
40
100 = 2
5
Don’t forget to cancel down, if possible

4. Converting between F, D & P
Converting a percentage to a decimal
67% means i.e. 67 ÷ 100
67
100
Remember ÷ by 100 ?
So,
67% = 0.67
1 1 1
H T U 10 100 1000
6 7

5. Converting between F, D & P
Converting a decimal to a percentage
Reverse the process i.e. X by 100
1 1 1
H T U 10 100 1000
0 4 3
So, 0.43 = 43%

6. Converting between F, D & P
Converting a fraction to a percentage
Convert to a decimal first then to a percentage i.e.
3 0 .6
5 =5
Then, change to a percentage, x by 100 3.00
So, 3 = 0.6 = 60%
5

7. Without a
Finding a Percentage - Calculator
10 1
Remember, 10% =
100 = 10
To find we ÷ by 10
1
10
Also, 1% =
1
100
And, to find we ÷ by 100
1
100

8. Without a
Finding a Percentage - Calculator
Use these facts to find any percentage
i.e. Find 32% of $240
10% = $24 and 1% = $2.40
So, 30% = 3 x $24 = $72
and 2% = 2 x $2.40 = $4.80
32% = $72.00 + 4.80 = $76.80

9. Without a
Finding a Percentage - Calculator
55% of 120 children at the theatre were boys, how many were
boys ?
10% = 12 and 1% = 1.2
So, 50% = 5 x 12 = 60
and 5% = 5 x 1.2 = 6
55% = 60 + 6 = 66 boys
(5% can also be found by using ½ of 10%)

10. With a
Finding a Percentage - Calculator
Change percentage to a decimal first
eg. Find 28% of 690
28% = 0.28 and “of” means multiply
So 28% of 690 is
0.28 x 690
Type into your calculator
Answer = 193.2

11. With a
Finding a Percentage - Calculator
Another example, find 17.5% of $250
So, 0.175 x 250
Type into calculator
Answer = $43.75
Find 32.5% of 1200 …
0.325 x 1200 =
390

12. Profit & Loss
2 types of question
Type 1 -
A car was bought for $1200 and was later sold at a 15%
profit, how much was it sold for ?
Find 15% and then add it on to $1200
If it were sold for a 24% loss
Find 24% and then take it off the $1200

13. Profit & Loss
Type 2 –
A car was bought for $1200 and later sold for $1500, what is
the percentage profit ?
Use the format
To create a fraction
Cancel to simplest form and then change to a percentage
Actual Profit (or Loss)
Original Amount

14. Profit & Loss
A car was bought for $1200 and later sold for $1400, what is
the percentage profit ?
200 1
Actual Profit
Original Amount
= 1200 = 6
0.1666
1
6 = 6 1.00 = 17%

15. Profit & Loss
A cycle was bought for $600 and later sold for $450, what is
the percentage loss ?
150 1
Actual Loss
Original Amount
= 600 = 4
0.25
1
4 = 4 1.00 = 25%

16. Reverse Percentages
The original amount is always 100%
A reduction of 20% means the new price is 80% of original
An increase of 15% means the new price is 115% of original
Use the calculator method to find original amount

17. Reverse Percentages
eg. In a 25% sale a sofa costs $480, how much did it cost
before the sale ?
25% reduction means 75% of original
i.e. 100% - 25% = 75%
x 0.75
Price before Price after
Sale ? Sale $480
÷ 0.75
So, $480 ÷ 0.75 = $640

18. Reverse Percentages
eg. Following a 10% increase petrol now costs $1.20 per
litre, how much did it cost before the increase ?
10% increase means 110% of original
x 1.10
Price before New Price
increase ?
So, $1.20 ÷ 1.10 = $1.09 per litre $1.20
÷ 1.10

19. Writing as a Percentage
One quantity as a percentage of another
eg. Aylish scored 32 out of 50 in a science test and 48 out of 80
in maths
Write as a fraction first, then cancel down
Science Maths
32 48
50 80
16 3
= 25 = 0.64 = 5 = 0.6
= 64% = 60%

20. Writing as a Percentage
What percentage of cars are Green ? Car Park Survey
22 out of 122 were green, so Colour Frequency
Green 22
Silver 43
Change to a decimal
Black 57
Then convert to a percentage
22
22
122
122 = 0.18
=18%

21. Session Summary
Converting between Fractions Decimals and Percentages
Finding a Percentage
Profit & Loss
Reverse Percentages
Writing as a Percentage
Next week - Ratio
21 14/03/13