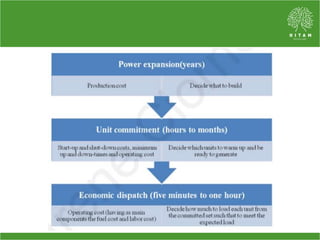
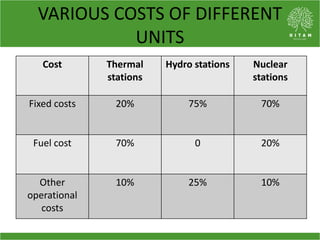
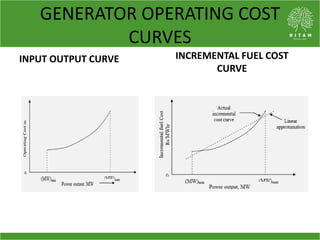
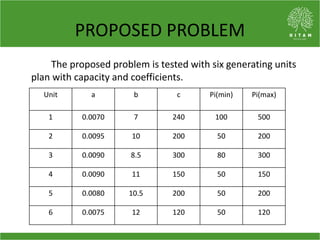
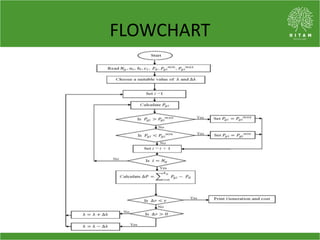
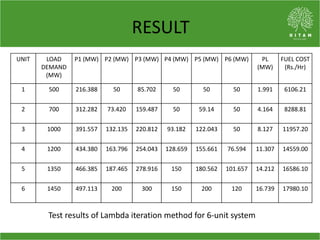
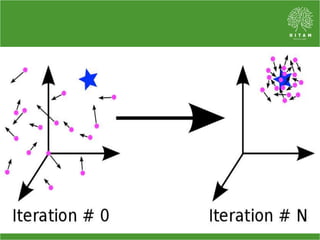
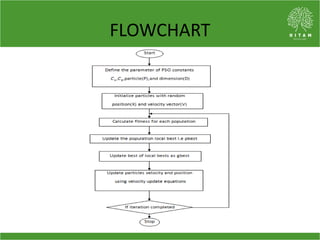
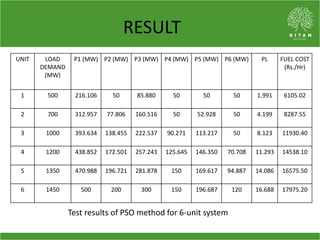
The document discusses the economic load dispatch problem in thermal power stations, aiming to minimize total fuel costs while meeting generation limits and operational constraints. It outlines various techniques, such as lambda iteration and particle swarm optimization (PSO), for solving this optimization problem, highlighting their respective efficiencies and results for a six-unit system. The conclusion notes that while the lambda method relies on initial values, PSO consistently yields converged solutions without such dependencies.

1. SOLUTION TO ECONOMIC LOAD
DISPATCH PROBLEM IN THERMAL
POWER STATIONS

2. OBJECTIVE
In this work our main aim is to find the optimal
solution to ‘Economic Load Dispatch’ including losses
and generating limits by minimizing the total fuel cost
while satisfying the constraints.
Economic Load Dispatch is defined as the process
of allocating generation levels to the generating units,
so that the system load may be supplied entirely and
most economically.

4. VARIOUS COSTS OF DIFFERENT
UNITS
Cost Thermal
stations
Hydro stations Nuclear
stations
Fixed costs 20% 75% 70%
Fuel cost 70% 0 20%
Other
operational
costs
10% 25% 10%

5. OPERATING COST OF THERMAL
PLANT
The total operating cost of thermal plant depends on
 Cost of labour
 Fuel cost
 Maintenance cost
But all these costs are difficult to determine. So, they are
assumed as a fixed percentage of fuel cost.

6. FUEL COST
In all practical cases, the fuel cost of generator can be
represented as a quadratic function of real power generation.
The total fuel cost equation is given by
where are cost coefficients

7. GENERATOR OPERATING COST
CURVES
INPUT OUTPUT CURVE INCREMENTAL FUEL COST
CURVE

8. OPERATING CONSTRAINTS
Constraints means limitations or basic operating conditions
in power system.
ACTIVE POWER CONSTRAINT
Pmin ≤ P ≤ Pmax
REACTIVE POWER CONSTRAINT
Qmin ≤ Q ≤ Qmax
VOLTAGE MAGNITUDE CONSTRAINT
|V|min ≤ |V| ≤ |V|max
LOAD ANGLE CONSTRAINT
δmin ≤ δ ≤ δmax

9. PROPOSED PROBLEM
The proposed problem is tested with six generating units
plan with capacity and coefficients.
Unit a b c Pi(min) Pi(max)
1 0.0070 7 240 100 500
2 0.0095 10 200 50 200
3 0.0090 8.5 300 80 300
4 0.0090 11 150 50 150
5 0.0080 10.5 200 50 200
6 0.0075 12 120 50 120

10. Cont...
Coefficients
B =

11. GENERAL OPTIMIZATION
TECHNIQUES
DETERMINISTIC ALGORITHMS
1. Lambda Iteration method
2. Newton- Raphson method
3. Gradient Method etc.
STOCHASTIC ALGORITHMS
1. Particle Swarm Optimization(PSO)
2. Artificial Bee Colony(ABC)
3. Genetic Algorithm(GA) etc.
These artificial intelligence methods solve optimization
problems very efficiently and often achieve a fast and reasonable
solution.

12. LAMBDA ITERATION METHOD
Lambdaiteration(LagrangianMultiplier)methodisthestandard
method to solve ELD problem which was introduced by Kuhn and
Tucker. This method is more conventional to deal with the
minimization of cost of generating the power at any demand. For
more number of units, the Lambda iteration method is more
accurate.

13. FLOWCHART

14. RESULT
UNIT LOAD
DEMAND
(MW)
P1 (MW) P2 (MW) P3 (MW) P4 (MW) P5 (MW) P6 (MW) PL
(MW)
FUEL COST
(Rs./Hr)
1 500 216.388 50 85.702 50 50 50 1.991 6106.21
2 700 312.282 73.420 159.487 50 59.14 50 4.164 8288.81
3 1000 391.557 132.135 220.812 93.182 122.043 50 8.127 11957.20
4 1200 434.380 163.796 254.043 128.659 155.661 76.594 11.307 14559.00
5 1350 466.385 187.465 278.916 150 180.562 101.657 14.212 16586.10
6 1450 497.113 200 300 150 200 120 16.739 17980.10
Test results of Lambda iteration method for 6-unit system

15. PARTICLE SWARM OPTIMIZATION
Particle swarm optimization (PSO) technique was first
introduced by Dr. Kennedy and Dr. Eberhart in 1995.
It is a flexible, robust, population based algorithm. This
method solves a variety of power systems problems due to its
simplicity, superior convergence characteristics and high
quality solution.

18. FLOWCHART

19. RESULT
UNIT LOAD
DEMAND
(MW)
P1 (MW) P2 (MW) P3 (MW) P4 (MW) P5 (MW) P6 (MW) PL FUEL COST
(Rs./Hr)
1 500 216.106 50 85.880 50 50 50 1.991 6105.02
2 700 312.957 77.806 160.516 50 52.928 50 4.199 8287.55
3 1000 393.634 138.455 222.537 90.271 113.217 50 8.123 11930.40
4 1200 438.852 172.501 257.243 125.645 146.350 70.708 11.293 14538.10
5 1350 470.988 196.721 281.878 150 169.617 94.887 14.086 16575.50
6 1450 500 200 300 150 196.687 120 16.688 17975.20
Test results of PSO method for 6-unit system

20. CONCLUSION
From the results it can be concluded that, the lambda
iterative method heavily depends on the selection of initial
value. Whereas PSO technique always provides converged
solution which does not require initial value of lambda.