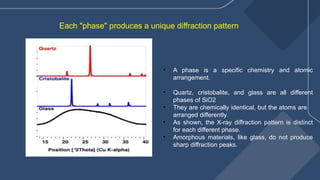
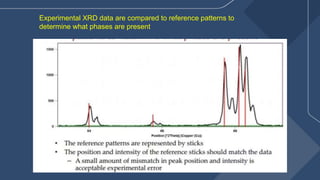
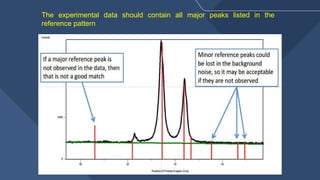
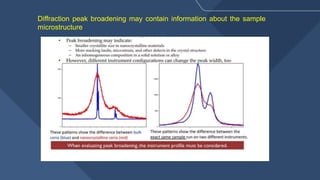
The document presents a detailed overview of X-ray diffraction (XRD), a technique for analyzing the crystallographic structure of materials. It covers the principles of XRD, its historical background, applications, and the equipment used in the process, highlighting its non-destructive nature and accuracy in determining structural properties. Key concepts such as Bragg's law, diffraction peaks, and the importance of crystallography are also discussed.