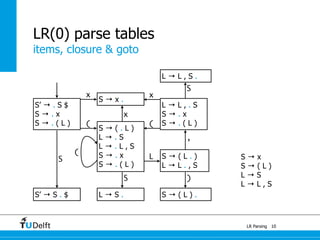
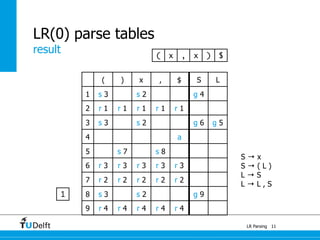
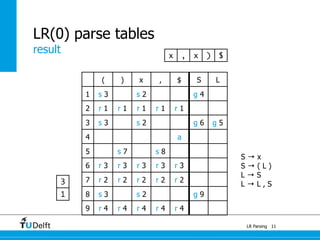
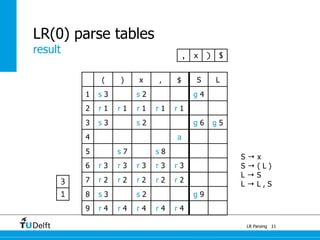
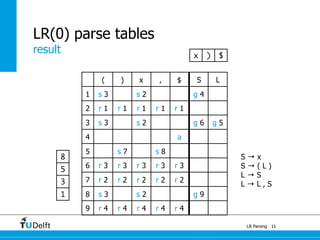
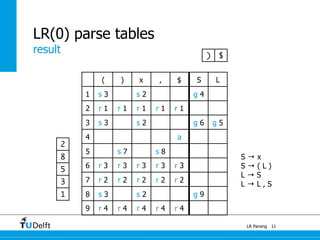
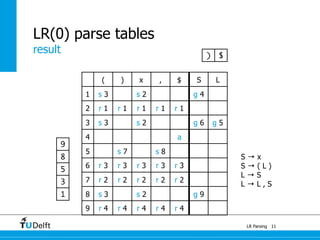
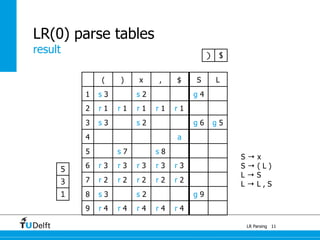
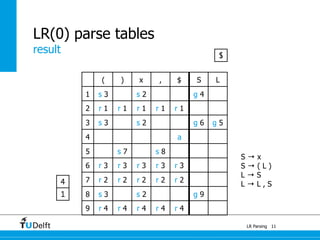
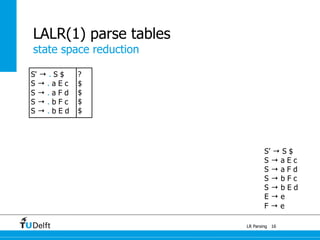
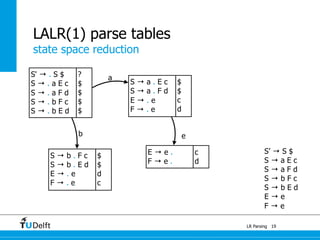
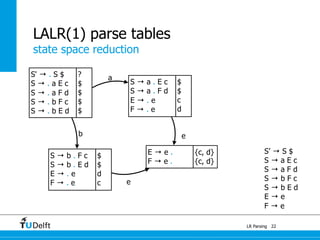
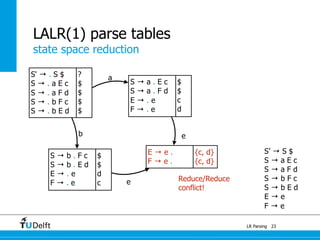
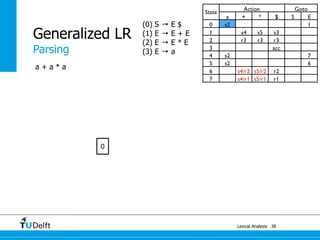
LR parsing allows parsers to see the entire right-hand side of a rule and perform lookahead, allowing it to handle a wider range of grammars than LL parsing. The document provides an example of LR parsing a simple expression grammar. It demonstrates the steps of building the LR parsing items, closure, and goto functions to generate the LR parsing table from the grammar. LR parsing tables contain the states, symbols, and parsing actions (reduce, shift, accept).
















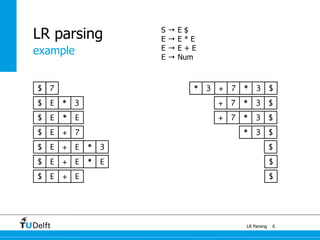
















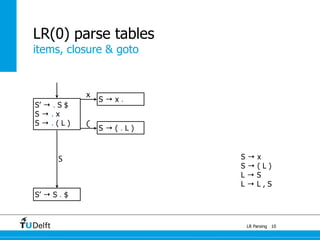






















































![0
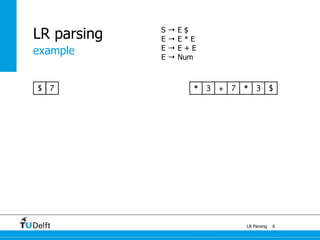
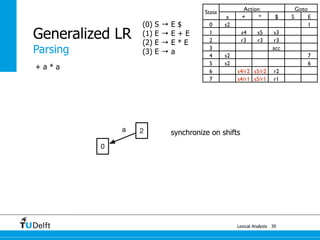
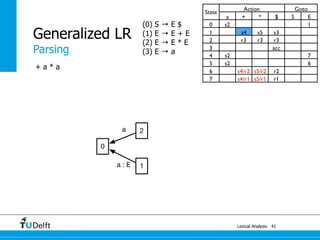
1a : E 4
+
a : E
7
1a + a : E
5
*
*
6
a : E
7
a * a : E
1
[a + a] * a : E
Lexical Analysis
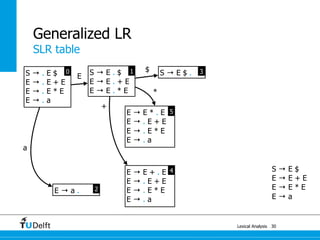
Generalized LR
56
Parsing
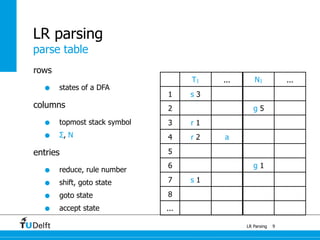
State
Action Goto
a + * $ S E
0 s2 1
1 s4 s5 s3
2 r3 r3 r3
3 acc
4 s2 7
5 s2 6
6 s4/r2 s5/r2 r2
7 s4/r1 s5/r1 r1
(0) S → E $
(1) E → E + E
(2) E → E * E
(3) E → a](https://image.slidesharecdn.com/cc-lr-parsing-170116134922/85/LR-Parsing-119-320.jpg)
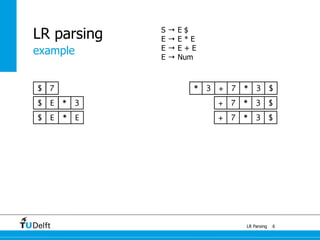
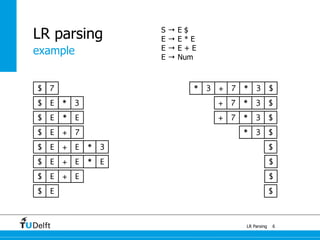
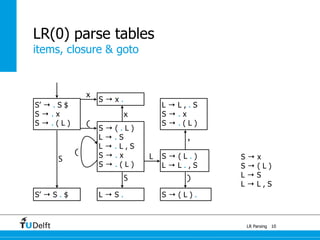
![0
1a : E 4
+
a : E
7
1a + a : E
5
*
*
6
a : E
7
a * a : E
1
[a + a] * a : E
Lexical Analysis
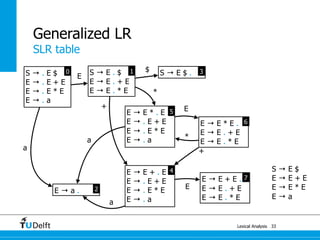
Generalized LR
57
Parsing
State
Action Goto
a + * $ S E
0 s2 1
1 s4 s5 s3
2 r3 r3 r3
3 acc
4 s2 7
5 s2 6
6 s4/r2 s5/r2 r2
7 s4/r1 s5/r1 r1
(0) S → E $
(1) E → E + E
(2) E → E * E
(3) E → a](https://image.slidesharecdn.com/cc-lr-parsing-170116134922/85/LR-Parsing-120-320.jpg)
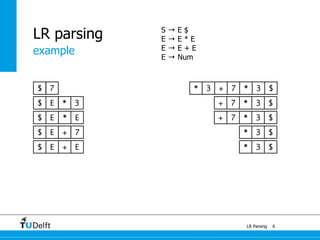
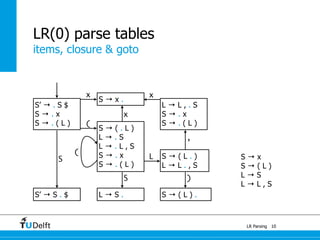
![[a + a] * a : E
or
a + [a * a] : E
0
1a : E 4
+
a : E
7
1a + a : E
5
*
*
6
a : E
7
a * a : E
1
Lexical Analysis
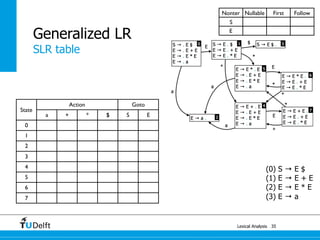
Generalized LR
58
Parsing
State
Action Goto
a + * $ S E
0 s2 1
1 s4 s5 s3
2 r3 r3 r3
3 acc
4 s2 7
5 s2 6
6 s4/r2 s5/r2 r2
7 s4/r1 s5/r1 r1
(0) S → E $
(1) E → E + E
(2) E → E * E
(3) E → a](https://image.slidesharecdn.com/cc-lr-parsing-170116134922/85/LR-Parsing-121-320.jpg)
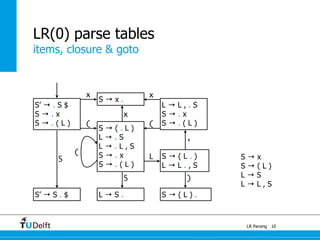
![[a + a] * a : E
or
a + [a * a] : E
0
1a : E 4
+
a : E
7
1a + a : E
5
*
*
6
a : E
7
a * a : E
1 3
$
Lexical Analysis
Generalized LR
59
Parsing
State
Action Goto
a + * $ S E
0 s2 1
1 s4 s5 s3
2 r3 r3 r3
3 acc
4 s2 7
5 s2 6
6 s4/r2 s5/r2 r2
7 s4/r1 s5/r1 r1
(0) S → E $
(1) E → E + E
(2) E → E * E
(3) E → a
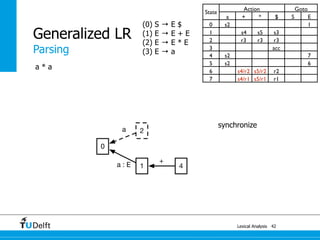
synchronize
accept with trees on the link to initial state](https://image.slidesharecdn.com/cc-lr-parsing-170116134922/85/LR-Parsing-122-320.jpg)


![Lexical Analysis
Scannerless Generalized LR
62
Normalization
context-free syntax
Exp.Add = <<Exp> + <Exp>> {left}
Exp.Inc = <<Exp>++>
Exp.ID = ID
lexical syntax
ID = [a-zA-Z] IDRest*
IDRest = [a-zA-Z0-9]
LAYOUT = [ tnr]
ID = "let" {reject}](https://image.slidesharecdn.com/cc-lr-parsing-170116134922/85/LR-Parsing-125-320.jpg)
![context-free syntax
Exp.Add = <<Exp> + <Exp>> {left}
Exp.Inc = <<Exp>++>
Exp.ID = ID
lexical syntax
ID = [a-zA-Z] IDRest*
IDRest = [a-zA-Z0-9]
LAYOUT = [ tnr]
ID = "let" {reject}
Lexical Analysis
Scannerless Generalized LR
63
Normalization
Exp-CF.Add = Exp-CF LAYOUT?-CF "+" LAYOUT?-CF Exp-CF {left}
Exp-CF.Inc = Exp-CF LAYOUT?-CF "++"
Exp-CF.ID = ID-CF
ID-LEX = [a-zA-Z] IDRest*-LEX
IDRest*-LEX = [a-zA-Z0-9]
ID-LEX = "let" {reject}
LAYOUT-CF = LAYOUT-LEX
Separate lexical from context-free symbols
and separate symbols in context-free syntax
by optional layout.](https://image.slidesharecdn.com/cc-lr-parsing-170116134922/85/LR-Parsing-126-320.jpg)
![Lexical Analysis
Scannerless Generalized LR
64
Normalization
LAYOUT-CF = LAYOUT-LEX
IDRest-CF = IDRest-LEX
IDRest*-CF = IDRest*-LEX
ID-CF = ID-LEX
context-free syntax
Exp.Add = <<Exp> + <Exp>> {left}
Exp.Inc = <<Exp>++>
Exp.ID = ID
lexical syntax
ID = [a-zA-Z] IDRest*
IDRest = [a-zA-Z0-9]
LAYOUT = [ tnr]
ID = "let" {reject}
Create injections from lexical to
context-free symbols](https://image.slidesharecdn.com/cc-lr-parsing-170116134922/85/LR-Parsing-127-320.jpg)
![Lexical Analysis
Scannerless Generalized LR
65
Normalization
"+" = [43]
"++" = [43] [43]
"let" = [108] [101] [116]
ID-LEX = [65-9097-122] IDRest*-LEX
IDRest*-LEX = [48-5765-9097-122]
LAYOUT-LEX = [9-101332]
context-free syntax
Exp.Add = <<Exp> + <Exp>> {left}
Exp.Inc = <<Exp>++>
Exp.ID = ID
lexical syntax
ID = [a-zA-Z] IDRest*
IDRest = [a-zA-Z0-9]
LAYOUT = [ tnr]
ID = "let" {reject}
Normalize literals symbols and
character classes.](https://image.slidesharecdn.com/cc-lr-parsing-170116134922/85/LR-Parsing-128-320.jpg)
![Lexical Analysis
Scannerless Generalized LR
66
Normalization
LAYOUT?-CF = LAYOUT-CF
LAYOUT?-CF =
IDRest+-LEX = IDRest-LEX
IDRest+-LEX = IDRest+-LEX IDRest-LEX
IDRest*-LEX =
IDRest*-LEX = IDRest+-LEX
IDRest+-CF = IDRest+-LEX
context-free syntax
Exp.Add = <<Exp> + <Exp>> {left}
Exp.Inc = <<Exp>++>
Exp.ID = ID
lexical syntax
ID = [a-zA-Z] IDRest*
IDRest = [a-zA-Z0-9]
LAYOUT = [ tnr]
ID = "let" {reject}
Normalize regular expressions.](https://image.slidesharecdn.com/cc-lr-parsing-170116134922/85/LR-Parsing-129-320.jpg)
![Lexical Analysis
Scannerless Generalized LR
67
Normalization
context-free start-symbols
Exp
<START> = LAYOUT?-CF Exp-CF LAYOUT?-CF
<Start> = <START> [256]
Define extra rules for the start symbols.](https://image.slidesharecdn.com/cc-lr-parsing-170116134922/85/LR-Parsing-130-320.jpg)















