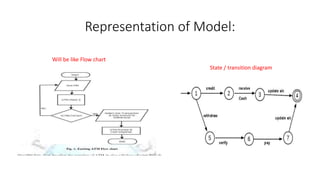
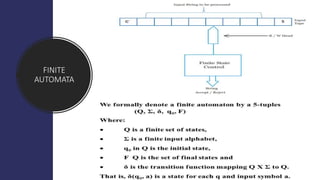
Theory of computation is the study of how problems can be solved using formal mathematical models of computation that reflect real-world computers. It includes automata theory, which studies abstract machines and how they can be used to solve problems. Models of computation are represented using tools like flow charts, state transition diagrams, and transition tables. Theory of computation has applications in areas like text processing, web browsing, compiler design, and artificial intelligence. It builds on fields like set theory, model theory, and computability theory. Key topics covered include finite automata, regular expressions and languages, context-free grammars and languages, and the undecidability of some computational problems.

1. Theory of Computation - Introduction

2. What do u mean by computation?
calculation, solving, making decision , any kind of operations/task by any machine
(like computer, calculator)
What do u mean by theory?
Simply speaking ….. A theory is a group of ideas intended to explain something.
logically speaking …. A theory is a fact-based framework for describing a phenomenon.
i.e basic principles behind any concept
Purpose of Theory of computation :
Develop formal mathematical models of computation that reflect real-world computers

3. Definition:
Theory of computation is the branch that deals with how effectively
problems can be solved on a model of computation, using an
algorithm.
Automata Theory:
• Automata is the plural of automaton – means automatic machine
• Is the study of abstract machines and how it could solve the
problems.

4. Representation of Model:
Will be like Flow chart
State / transition diagram

5. Applications of Automata
• Text processing – string search
• Web browsing
• Compiler design
• Operating system
• Game theory (strategy model by decision making)
• NLP
• Artificial intelligence

6. PREREQUISTIES
• Set theory
• Model theory
• Computability theory
• Proof theory

7. CS8501 Theory of Computation
UNIT I AUTOMATA FUNDAMENTALS
UNIT II REGULAR EXPRESSIONS AND LANGUAGES
UNIT III CONTEXT FREE GRAMMAR AND LANGUAGES
UNIT IV PROPERTIES OF CONTEXT FREE LANGUAGES
UNIT V UNDECIDABILITY

8. TEXTBOOK FOR REFERENCE

9. FINITE
AUTOMATA

10. REPRESENTATIONS
Transition function :
syntax: δ(state , input symbol) -> output state
example: δ(q0,1)= q1
2) Transition table
Row ---> states
Column ---> input symbols
1) Transition diagram

11. TYPES OF FA
1. Deterministic Finite Automata (DFA)
2. Non- Deterministic Finite Automata (NFA)
Both are defined by 5 tuples but there is difference in :
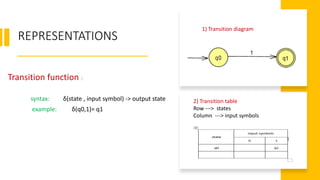
Transition function
DFA: Q x Σ -> [Q] - output is single state
NFA : Q x Σ -> {Q} - output is in many states

12. NFA
δ(q0,b)= {q0,q1}
NFA
δ(q0,1)= {q0,q2}
δ(q0,0)= {q0,q1}
δ(q2,1)= {q3}
δ(q2,1)= ∅
DFA
δ(q0,b)= [q0]
δ(q0,a)=[ q0,q1]
∅ - no null transitions
Guess the type of FA