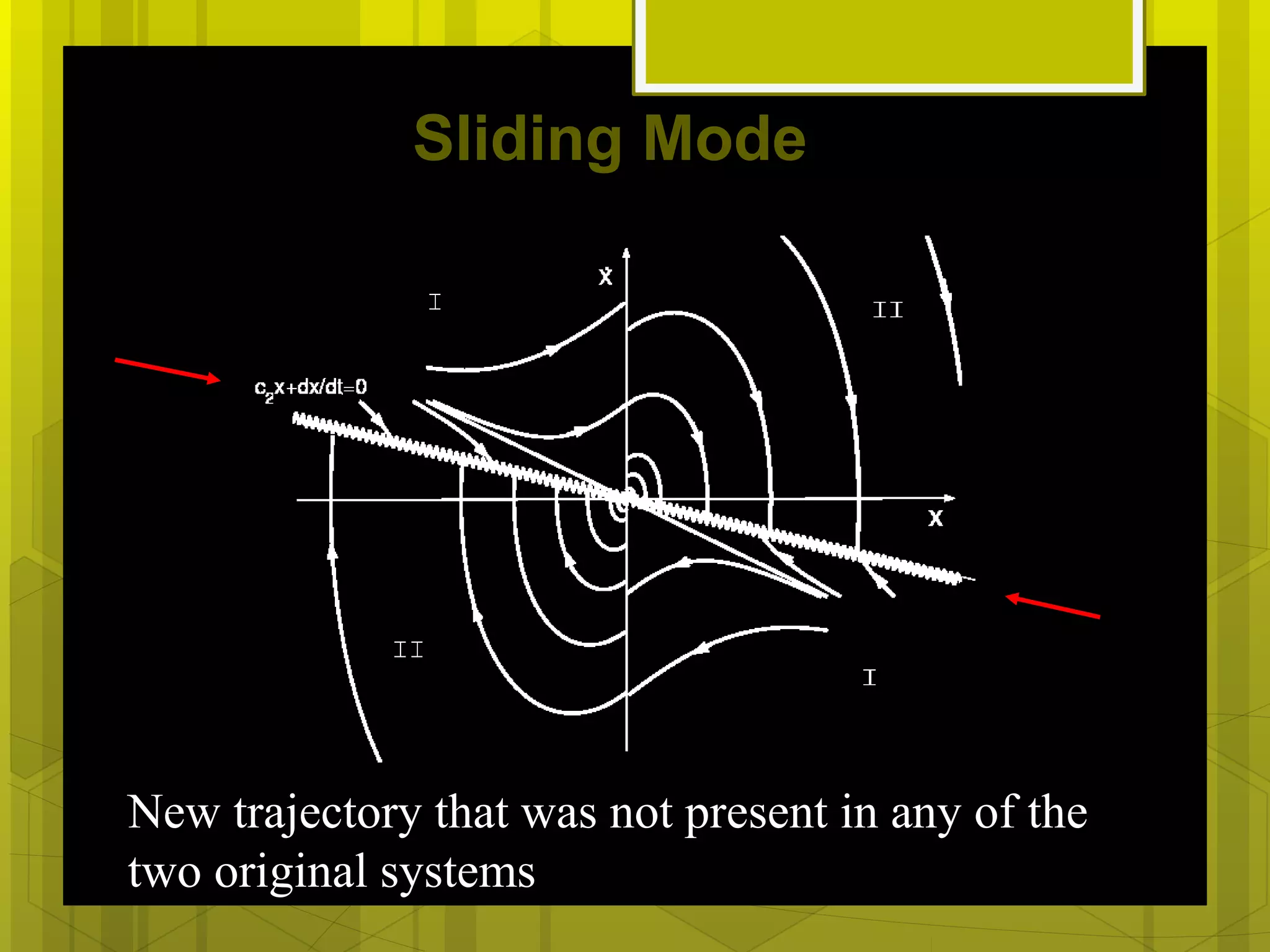
Variable structure control is a form of discontinuous nonlinear control that alters system dynamics through high-frequency switching. It achieves asymptotically stable behavior not present in unstable constituent systems. Sliding mode control is a type of variable structure control that drives the system state along a chosen sliding surface. While providing robustness, sliding mode induces undesirable chattering that actuates unmodeled dynamics. Chattering is reduced by smoothing the discontinuous control law, though this risks losing the sliding mode.

2. Variable Structure Control
• Variable structure control (VSC) is a form
of discontinuous nonlinear control.
• The method alters the dynamics of
a nonlinear system by application of a high-
frequency switching control.
• The state-feedback control law
is not a continuous function of time.

3. Variable Structure Control –
Constituent Systems
Mode 1
Mode 2
1x a x 
2
2 10
x a x
a a
 
 

4. Piecing together

5. Properties of VSC
►Both constituent systems were oscillatory
and were not asymptotically stable.
►‘Combined’ system is asymptotically stable.
►Property not present in any of the constituent
system is obtained by VSC

6. Another Example – Unstable
Constituent Systems
0x x x   0x x x   

7. Analysis
►Both systems are unstable
►Only stable mode is one mode of system
►IF the following VSC is employed
2
0,
2 4
x x x
 
        
0
, * , *
0
I xs
Mode s c x x c
II xs


    


8. Combined

9. In this case
►Again, property not present in constituent systems
is found in the combined system.
►A stable structure can be obtain by varying
between two unstable structures.
►However, a more interesting behavior can be
observed if we use a different ‘switching’ logic.
2 2
0
, ,0 *
0
I xs
Mode s c x x c c
II xs

    


10. The Region

11. Sliding Mode
New trajectory that was not present in any of the
two original systems

12. Sliding mode?
►Defined : Motion of the system trajectory along a
‘chosen’ line/plane/surface of the state space.
►Sliding Mode Control : Control designed with the
aim to achieve sliding mode.
 Is usually of VSC type
Eg : Previous problem can be perceived as
0
sgn( )
x x u
u xs x


  
 

13. Design of Sliding Mode Control
 Phase 1 (Sliding Surface Design):
Constructing Switching Surfaces so that the
system restricted to the switching surface
produces a desired behavior.
 Phase 2 (Controller Design):
Constructing switched feedback gains which
drive the plant state trajectory to the sliding
surface and maintain it there.

14. Advantage of SMC
Robustness
Nonlinear Structures
Uses information about input as well as output
feedback in control determination.
It is an open-closed-loop type control.
Improve performance based on computed torque
Insensitive to the uncertainties variation

15. Required Property
►For sliding mode to be of any use, it should have
the following properties
System stability confined to sliding surface
(unstable sliding mode is NOT sliding mode at
all)
Sliding mode should not take ‘forever’ to start
Disadvantages:
Very large control effort

16. The Chattering Problem
►When, s is very close to zero, the control signal
switches between two structures.
►Theoretically, the switching causes zero
magnitude oscillations with infinite frequency in x.
►Practically, actuators cannot switch at infinite
frequency. So we have high frequency oscillations
of non-zero magnitude.
►This undesirable phenomenon is called chattering.

17. Response
Ideal Sliding Mode
Practical – With
Chattering

18. Why is chattering undesirable?
►The ‘high frequency’ of chattering actuates un-
modeled high frequency dynamics of the system.
Controller performance deteriorates.
►More seriously, high frequency oscillations can
cause mechanical wear in the system.

19. Chattering Avoidance/Reduction
►The chattering problem is because signum
function is used in control.
Control changes very abruptly near s=0.
Actuator tries to cope up leading to ‘maximum-
possible-frequency’ oscillations.
►Solution :
Replace signum term in control by ‘smoother’
choices’

20. Disadvantage of ‘smoothing’
►If saturation or tanh is used, then we can observe
that near s=0
►
►Where represents the saturation or tanh
function.
►The limit in both cases is zero.
►So, technically the sliding mode is lost
0
( )lim
s
s
kf s
s
 
( )f s

21. QUESTIONS