Simpleharmonicmotion
•Download as PPTX, PDF•
0 likes•162 views
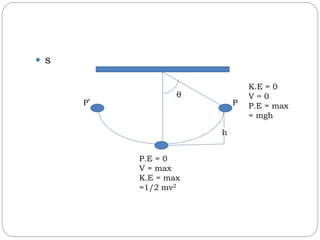
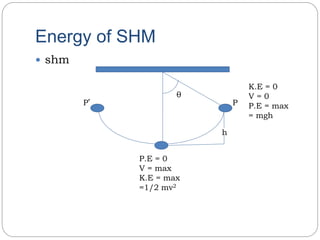
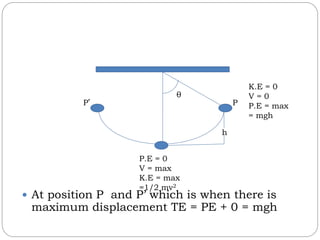
This document discusses simple harmonic motion and provides useful formulas. It explains that the period of a simple pendulum is calculated as T = 2π√l/g, where T is the period, l is the length of the pendulum, and g is the acceleration due to gravity. For an elastic spring undergoing simple harmonic motion, the total energy is calculated as the kinetic energy (1/2mv^2) plus the potential energy (1/2kx^2), where k is the spring constant. The document also states that the total energy is equal to the maximum potential energy when the kinetic energy is zero, and equal to the maximum kinetic energy when the potential energy is zero.
Report
Share
Report
Share
Recommended
2 law and exergy change
The document discusses second law efficiencies and exergy change of systems. It defines second law efficiency for various devices like heat engines, work-producing devices, refrigerators, and general processes. Second law efficiency compares the actual performance of a device to its theoretical maximum performance under reversible conditions. The exergy change of a closed system depends on the change in internal energy, pressure-volume work, and entropy between initial and final states, accounting for environmental properties. Exergy can represent the useful or recoverable work of a system.
Availability
The document discusses high grade and low grade energy sources. High grade energy sources include mechanical, electrical, water, wind and tidal power which can be completely converted to work without loss. Low grade energy sources like heat can only partially be converted to work. Low grade energy consists of exergy (available energy) and anergy (unavailable energy). The maximum useful work obtainable from a heat source is called its availability or exergy. The minimum energy that must be rejected according to the second law of thermodynamics is called anergy. Availability reduces as the temperature difference between a system and its surroundings decreases.
introduction chapter Eme or thermodynamics
Prime movers use natural resources like fuel, flowing water, or atoms to convert their energy into mechanical or useful work. They change various forms of energy including mechanical, thermal, electromagnetic, electrical, nuclear, and chemical energy. Energy is defined as the ability to do work and is found in potential, kinetic, gravitational potential, elastic potential, and chemical potential forms. Common devices that convert one form of energy to another include engines and generators.
03 part3 availability irreversibility
This document discusses availability and irreversibility in transient and steady flow systems. It provides definitions for available energy, unavailable energy, dead state, and effectiveness. It examines availability in terms of the first and second laws of thermodynamics. Equations are given for calculating maximum work, availability, and irreversibility for various thermodynamic processes involving changes in temperature, pressure, and volume. Two sample problems are included and solved to demonstrate calculating work, availability change, and irreversibility for specified thermodynamic systems.
Lecture 15 first law of thermodynamics
1) The document discusses the first law of thermodynamics and key concepts like internal energy, state variables, work, and heat transfer.
2) Internal energy depends on molecular kinetic and potential energy and can vary for different systems like monoatomic gases, diatomic gases, and monoatomic solids.
3) Work is defined as the area under a pressure-volume curve and can cause a change in the internal energy of a system according to the first law of thermodynamics.
4) For a cyclic process returning a system to its initial state, the total work done and heat transferred can be used to determine if energy was absorbed or released over the full cycle.
Cy101 thermodynamics
1. The first law of thermodynamics states that energy is conserved and can be changed from one form to another, but not created or destroyed. It describes the relationships between heat, work, and changes in internal energy of a system.
2. Enthalpy (H) is a state function that represents the total energy of a system at constant pressure. For a chemical reaction, the heat exchanged is equal to the change in enthalpy.
3. For an ideal gas undergoing an adiabatic (no heat exchange) process, the change in internal energy is equal to the pressure-volume work done, according to the first law of thermodynamics. The temperature of the gas decreases during expansion
Thermodynamics relations
This document discusses thermodynamic properties and relations. Some key points:
- Thermodynamic properties that cannot be directly measured must be related to measurable properties.
- Properties are continuous point functions that have exact differentials and can be written as functions of two independent variables like z(x,y).
- The Maxwell relations relate the partial derivatives of properties like pressure, specific volume, temperature and entropy.
- The Clapeyron equation relates the enthalpy change of phase change to the slope of the saturation curve on a pressure-temperature diagram.
- Specific heats, internal energy, enthalpy and entropy changes can be expressed in terms of pressure, specific volume, temperature and specific he
First law of thermodynamics
1. The document discusses concepts from engineering chemistry including the laws of thermodynamics, kinetics, and related topics.
2. It explains key thermodynamic concepts such as state functions, path functions, the four laws of thermodynamics, entropy, enthalpy, and Gibbs free energy.
3. The document also discusses kinetic concepts such as activation energy, the Arrhenius equation, and enzyme catalysis using the Michaelis-Menten mechanism.
Recommended
2 law and exergy change
The document discusses second law efficiencies and exergy change of systems. It defines second law efficiency for various devices like heat engines, work-producing devices, refrigerators, and general processes. Second law efficiency compares the actual performance of a device to its theoretical maximum performance under reversible conditions. The exergy change of a closed system depends on the change in internal energy, pressure-volume work, and entropy between initial and final states, accounting for environmental properties. Exergy can represent the useful or recoverable work of a system.
Availability
The document discusses high grade and low grade energy sources. High grade energy sources include mechanical, electrical, water, wind and tidal power which can be completely converted to work without loss. Low grade energy sources like heat can only partially be converted to work. Low grade energy consists of exergy (available energy) and anergy (unavailable energy). The maximum useful work obtainable from a heat source is called its availability or exergy. The minimum energy that must be rejected according to the second law of thermodynamics is called anergy. Availability reduces as the temperature difference between a system and its surroundings decreases.
introduction chapter Eme or thermodynamics
Prime movers use natural resources like fuel, flowing water, or atoms to convert their energy into mechanical or useful work. They change various forms of energy including mechanical, thermal, electromagnetic, electrical, nuclear, and chemical energy. Energy is defined as the ability to do work and is found in potential, kinetic, gravitational potential, elastic potential, and chemical potential forms. Common devices that convert one form of energy to another include engines and generators.
03 part3 availability irreversibility
This document discusses availability and irreversibility in transient and steady flow systems. It provides definitions for available energy, unavailable energy, dead state, and effectiveness. It examines availability in terms of the first and second laws of thermodynamics. Equations are given for calculating maximum work, availability, and irreversibility for various thermodynamic processes involving changes in temperature, pressure, and volume. Two sample problems are included and solved to demonstrate calculating work, availability change, and irreversibility for specified thermodynamic systems.
Lecture 15 first law of thermodynamics
1) The document discusses the first law of thermodynamics and key concepts like internal energy, state variables, work, and heat transfer.
2) Internal energy depends on molecular kinetic and potential energy and can vary for different systems like monoatomic gases, diatomic gases, and monoatomic solids.
3) Work is defined as the area under a pressure-volume curve and can cause a change in the internal energy of a system according to the first law of thermodynamics.
4) For a cyclic process returning a system to its initial state, the total work done and heat transferred can be used to determine if energy was absorbed or released over the full cycle.
Cy101 thermodynamics
1. The first law of thermodynamics states that energy is conserved and can be changed from one form to another, but not created or destroyed. It describes the relationships between heat, work, and changes in internal energy of a system.
2. Enthalpy (H) is a state function that represents the total energy of a system at constant pressure. For a chemical reaction, the heat exchanged is equal to the change in enthalpy.
3. For an ideal gas undergoing an adiabatic (no heat exchange) process, the change in internal energy is equal to the pressure-volume work done, according to the first law of thermodynamics. The temperature of the gas decreases during expansion
Thermodynamics relations
This document discusses thermodynamic properties and relations. Some key points:
- Thermodynamic properties that cannot be directly measured must be related to measurable properties.
- Properties are continuous point functions that have exact differentials and can be written as functions of two independent variables like z(x,y).
- The Maxwell relations relate the partial derivatives of properties like pressure, specific volume, temperature and entropy.
- The Clapeyron equation relates the enthalpy change of phase change to the slope of the saturation curve on a pressure-temperature diagram.
- Specific heats, internal energy, enthalpy and entropy changes can be expressed in terms of pressure, specific volume, temperature and specific he
First law of thermodynamics
1. The document discusses concepts from engineering chemistry including the laws of thermodynamics, kinetics, and related topics.
2. It explains key thermodynamic concepts such as state functions, path functions, the four laws of thermodynamics, entropy, enthalpy, and Gibbs free energy.
3. The document also discusses kinetic concepts such as activation energy, the Arrhenius equation, and enzyme catalysis using the Michaelis-Menten mechanism.
Lecture 3-4: Exergy, Heating and Cooling, Solar Thermal
The document discusses various topics related to energy and thermodynamics, including:
1) Different systems that can store 1 kW hr of energy and why we pay more for some forms.
2) The concept of exergy, which quantifies how useful energy is, and how it is lost as heat is converted to less useful forms.
3) Examples of heat engines and refrigerators/heat pumps, and calculations of their maximum possible efficiencies.
4) Ways of improving energy efficiency for heating, such as reducing heat loss, increasing heat pump coefficients of performance, and using combined heat and power systems.
First Law of Thermodynamics
First law of thermodynamics as taught in introductory physical chemistry (includes general chemistry material). Covers concepts such as internal energy, heat, work, heat capacity, enthalpy, bomb calorimetry, Hess's law, thermochemical equations, bond energy, and heat of formations.
Module 4 (first law of thermodynamics) 2021 2022
The document discusses the first law of thermodynamics, also known as the law of conservation of energy. It states that energy cannot be created or destroyed, only converted from one form to another. The first law is expressed mathematically as: Energy In - Energy Out = Change in Stored Energy. The document provides examples of applying the first law to closed and open systems, including deriving equations relating heat, work, internal energy, and other properties. It also includes examples solving thermodynamics problems for systems like turbines, compressors, and nozzles.
Second Law of Thermodynamics
Second law of thermodynamics (and third law of thermodynamics) as taught in introductory physical chemistry (including general chemistry). Covers concepts such as entropy, Gibbs free energy, and phase equilibrium.
Thermodynamics, part 8
The document discusses Gibbs free energy (G), which is a measure of the useful energy in a chemical reaction. A reaction will occur spontaneously if G decreases. G is defined as enthalpy (H) minus temperature (T) multiplied by entropy (S). The Gibbs free energy change (ΔG) for a reaction determines whether it is spontaneous or not. If ΔG is negative, the reaction proceeds spontaneously, and if ΔG is positive or zero, the reaction is at equilibrium or non-spontaneous. The Clapeyron equation relates the change in vapor pressure of a substance to temperature and can be used to calculate phase diagrams.
Thermodynamic relations, Clausius Clapreyon equation , joule thomson coefficient
Thermodynamic relations, Clausius Clapreyon equation , joule thomson coefficientPEC University Chandigarh
thermodynamic relation,lausius Clapreyon equation , joule thomson coefficient, specific heat relations ,
Thermodynamic, part 2
Ideal gases approximate the behavior of real gases at low pressures and densities. The kinetic theory of gases describes ideal gases as large numbers of tiny particles that move freely and undergo elastic collisions. The kinetic theory assumptions lead to simple relationships between pressure, volume, temperature, and number of moles or particles for ideal gases. The van der Waals equation accounts for the finite size of gas particles and their intermolecular attractions, better describing the behavior of real gases that deviate from ideal gas behavior at high pressures and low temperatures.
THERMODYNAMICS UNIT - IV
This document discusses ideal gases and how they differ from real gases. It provides an introduction to ideal gases, noting their key characteristics and assumptions. The document then covers the ideal gas law and how it combines Boyle's, Charles', and Gay-Lussac's laws. Real gases are described as deviating from ideal behavior, especially near their critical point. Equations for both ideal and real gases are presented. The concepts of reduced properties and the principle of corresponding states for comparing real gases are also summarized.
Thermodynamics note chapter:6 Entropy
1) Entropy is a thermodynamic property that is a measure of the molecular disorder or randomness of a system.
2) The second law of thermodynamics states that the entropy of an isolated system can never decrease, and will increase for irreversible processes.
3) For any natural process, the entropy of the universe increases due to irreversibilities, as entropy generation is always positive for real processes.
04 part1 general thermodynamic properties
The document discusses several thermodynamic concepts and relationships including:
1) The Helmholtz and Gibbs free energy functions, which relate the work done, internal energy, temperature, and entropy or enthalpy of a system.
2) Gibbs phase equilibrium condition, which states that for a system at constant temperature and pressure, the equilibrium state is the one that minimizes the Gibbs free energy.
3) The Clausius-Clapeyron equation, which describes the relationship between pressure and temperature during a phase change at constant temperature.
Thermodynamics
Thermodynamics deals with energy transformation between heat and work. A system is a specified region being studied, and can be open or closed to matter flow. The surroundings are outside the system boundary. A process is a change in a substance's state. A cycle occurs when the initial and final states are the same. The first law of thermodynamics states that energy cannot be created or destroyed, only converted between forms.
Thermal 05
The document discusses the concept of enthalpy in thermodynamics, defining it as a measure of the total energy of a system equal to the internal energy plus the product of pressure and volume. It provides the equation for enthalpy as H = U + pV, where H is enthalpy, U is internal energy, p is pressure, and V is volume. Examples are given to illustrate calculating work done by a gas and determining temperature, mass, internal energy change, and enthalpy change for a gas undergoing a constant volume heating process.
Thermodynamic, examples a
The document provides examples and problems related to thermodynamics. Example 1 involves calculating the final temperature of a system consisting of a brass block and ice water. Example 2 calculates the root mean square speeds of nitrogen and oxygen molecules in air. Example 3 determines the new temperature of an ideal gas that is compressed.
Termodinamika
Thermodynamics describes the relationship between heat and work for a system and its surroundings. A system is separated from its surroundings by walls that may allow heat transfer (diathermal) or not (adiabatic). A system's state is specified by properties like pressure, volume, temperature, and mass. The zeroth law states that if two systems are in thermal equilibrium with a third, they are in equilibrium with each other. The first law relates changes in a system's internal energy to heat and work. Thermal processes like isobaric, isochoric, isothermal, and adiabatic involve constant pressure, volume, temperature, or no heat transfer respectively.
Lecture 14 maxwell-boltzmann distribution. heat capacities
This document discusses molecular speeds and distributions, heat capacities, and phase diagrams. It begins by describing the Maxwell-Boltzmann distribution of molecular speeds and how temperature affects this. It then discusses how to calculate the molar heat capacity for monoatomic and diatomic ideal gases using the equipartition theorem. Finally, it introduces phase diagrams and uses examples like water, carbon dioxide, and nitrogen to illustrate different phase boundaries and triple points on pressure-temperature diagrams.
Thermodynamic I
process, Thermodynamic process,workdone, relation between pressure volume,first law of thermodynamic,need of second law,statement of second law,carnot heat engine,efficiency,numericals
Thermodynamics, part 3.ppt
The document discusses the first law of thermodynamics. It provides equations and explanations for how the internal energy (U) of a system can change through heat (Q) added or removed from the system or work (W) done on or by the system. The first law is expressed as ΔU = Q - W. Specific processes discussed include adiabatic (no heat transfer), isobaric (constant pressure), isochoric (constant volume), and isothermal (constant temperature). Diagrams are used to illustrate these concepts and how to calculate work from changes in pressure and volume.
Thermodynamic notes 2
The first law of thermodynamics states that energy can be transformed from one form to another, but cannot be created or destroyed. It provides a necessary but not sufficient condition for a process to occur. The first law was established through experiments by Joule showing that work input is proportional to heat output. The first law applies to closed systems and describes the various forms energy can take, such as work, heat, internal energy, and how changes in these forms are related through the principle of conservation of energy.
Thermodynamics note chapter:4 First law of Thermodynamics
The document summarizes the first law of thermodynamics. It states that the first law, also known as the law of conservation of energy, provides a basis for relating different forms of energy and their interactions during processes. The first law states that energy cannot be created or destroyed, only changed from one form to another. For closed systems, the total energy change is equal to the net heat transfer minus the net work. For open systems, the energy change also accounts for energy entering or leaving with mass flows. The document provides several examples of applying the first law to common thermodynamic processes.
Availability and irreversibility
(1) Availability analyses determine the maximum work possible from a device given a fuel amount. (2) Available energy is the maximum portion convertible to useful work by ideal processes reducing the system to equilibrium. The remainder is unavailable energy. (3) The theoretical maximum work from a system at state p1, T1 operating with a reservoir at p0, T0 is called availability. (4) Availability accounts for both work against resisting forces and the environment.
Consulting cardiologist may reduce the effect of drugs in take
The medications are recommended to diminish mid-section torment so patients whose hearts still contract regularly may feel sufficiently great to build their every day exercises. Presently, new research recommends the inverse is valid.
FINALPublicSpaceinJapan_FINAL_080312
This document catalogs and analyzes different typologies of public space in Japan. It discusses the layered complexity of Tokyo's urban form, with large modern architecture integrated into traditional neighborhoods. Public space takes many forms and scales, from small alleyways to large plazas, shaped by cultural and historical contexts as well as modern development. The document outlines the methodology used during a study abroad program to observe over 50 public spaces across Tokyo and Kyoto based on their functions, scales, dimensions, and other defining elements.
More Related Content
What's hot
Lecture 3-4: Exergy, Heating and Cooling, Solar Thermal
The document discusses various topics related to energy and thermodynamics, including:
1) Different systems that can store 1 kW hr of energy and why we pay more for some forms.
2) The concept of exergy, which quantifies how useful energy is, and how it is lost as heat is converted to less useful forms.
3) Examples of heat engines and refrigerators/heat pumps, and calculations of their maximum possible efficiencies.
4) Ways of improving energy efficiency for heating, such as reducing heat loss, increasing heat pump coefficients of performance, and using combined heat and power systems.
First Law of Thermodynamics
First law of thermodynamics as taught in introductory physical chemistry (includes general chemistry material). Covers concepts such as internal energy, heat, work, heat capacity, enthalpy, bomb calorimetry, Hess's law, thermochemical equations, bond energy, and heat of formations.
Module 4 (first law of thermodynamics) 2021 2022
The document discusses the first law of thermodynamics, also known as the law of conservation of energy. It states that energy cannot be created or destroyed, only converted from one form to another. The first law is expressed mathematically as: Energy In - Energy Out = Change in Stored Energy. The document provides examples of applying the first law to closed and open systems, including deriving equations relating heat, work, internal energy, and other properties. It also includes examples solving thermodynamics problems for systems like turbines, compressors, and nozzles.
Second Law of Thermodynamics
Second law of thermodynamics (and third law of thermodynamics) as taught in introductory physical chemistry (including general chemistry). Covers concepts such as entropy, Gibbs free energy, and phase equilibrium.
Thermodynamics, part 8
The document discusses Gibbs free energy (G), which is a measure of the useful energy in a chemical reaction. A reaction will occur spontaneously if G decreases. G is defined as enthalpy (H) minus temperature (T) multiplied by entropy (S). The Gibbs free energy change (ΔG) for a reaction determines whether it is spontaneous or not. If ΔG is negative, the reaction proceeds spontaneously, and if ΔG is positive or zero, the reaction is at equilibrium or non-spontaneous. The Clapeyron equation relates the change in vapor pressure of a substance to temperature and can be used to calculate phase diagrams.
Thermodynamic relations, Clausius Clapreyon equation , joule thomson coefficient
Thermodynamic relations, Clausius Clapreyon equation , joule thomson coefficientPEC University Chandigarh
thermodynamic relation,lausius Clapreyon equation , joule thomson coefficient, specific heat relations ,
Thermodynamic, part 2
Ideal gases approximate the behavior of real gases at low pressures and densities. The kinetic theory of gases describes ideal gases as large numbers of tiny particles that move freely and undergo elastic collisions. The kinetic theory assumptions lead to simple relationships between pressure, volume, temperature, and number of moles or particles for ideal gases. The van der Waals equation accounts for the finite size of gas particles and their intermolecular attractions, better describing the behavior of real gases that deviate from ideal gas behavior at high pressures and low temperatures.
THERMODYNAMICS UNIT - IV
This document discusses ideal gases and how they differ from real gases. It provides an introduction to ideal gases, noting their key characteristics and assumptions. The document then covers the ideal gas law and how it combines Boyle's, Charles', and Gay-Lussac's laws. Real gases are described as deviating from ideal behavior, especially near their critical point. Equations for both ideal and real gases are presented. The concepts of reduced properties and the principle of corresponding states for comparing real gases are also summarized.
Thermodynamics note chapter:6 Entropy
1) Entropy is a thermodynamic property that is a measure of the molecular disorder or randomness of a system.
2) The second law of thermodynamics states that the entropy of an isolated system can never decrease, and will increase for irreversible processes.
3) For any natural process, the entropy of the universe increases due to irreversibilities, as entropy generation is always positive for real processes.
04 part1 general thermodynamic properties
The document discusses several thermodynamic concepts and relationships including:
1) The Helmholtz and Gibbs free energy functions, which relate the work done, internal energy, temperature, and entropy or enthalpy of a system.
2) Gibbs phase equilibrium condition, which states that for a system at constant temperature and pressure, the equilibrium state is the one that minimizes the Gibbs free energy.
3) The Clausius-Clapeyron equation, which describes the relationship between pressure and temperature during a phase change at constant temperature.
Thermodynamics
Thermodynamics deals with energy transformation between heat and work. A system is a specified region being studied, and can be open or closed to matter flow. The surroundings are outside the system boundary. A process is a change in a substance's state. A cycle occurs when the initial and final states are the same. The first law of thermodynamics states that energy cannot be created or destroyed, only converted between forms.
Thermal 05
The document discusses the concept of enthalpy in thermodynamics, defining it as a measure of the total energy of a system equal to the internal energy plus the product of pressure and volume. It provides the equation for enthalpy as H = U + pV, where H is enthalpy, U is internal energy, p is pressure, and V is volume. Examples are given to illustrate calculating work done by a gas and determining temperature, mass, internal energy change, and enthalpy change for a gas undergoing a constant volume heating process.
Thermodynamic, examples a
The document provides examples and problems related to thermodynamics. Example 1 involves calculating the final temperature of a system consisting of a brass block and ice water. Example 2 calculates the root mean square speeds of nitrogen and oxygen molecules in air. Example 3 determines the new temperature of an ideal gas that is compressed.
Termodinamika
Thermodynamics describes the relationship between heat and work for a system and its surroundings. A system is separated from its surroundings by walls that may allow heat transfer (diathermal) or not (adiabatic). A system's state is specified by properties like pressure, volume, temperature, and mass. The zeroth law states that if two systems are in thermal equilibrium with a third, they are in equilibrium with each other. The first law relates changes in a system's internal energy to heat and work. Thermal processes like isobaric, isochoric, isothermal, and adiabatic involve constant pressure, volume, temperature, or no heat transfer respectively.
Lecture 14 maxwell-boltzmann distribution. heat capacities
This document discusses molecular speeds and distributions, heat capacities, and phase diagrams. It begins by describing the Maxwell-Boltzmann distribution of molecular speeds and how temperature affects this. It then discusses how to calculate the molar heat capacity for monoatomic and diatomic ideal gases using the equipartition theorem. Finally, it introduces phase diagrams and uses examples like water, carbon dioxide, and nitrogen to illustrate different phase boundaries and triple points on pressure-temperature diagrams.
Thermodynamic I
process, Thermodynamic process,workdone, relation between pressure volume,first law of thermodynamic,need of second law,statement of second law,carnot heat engine,efficiency,numericals
Thermodynamics, part 3.ppt
The document discusses the first law of thermodynamics. It provides equations and explanations for how the internal energy (U) of a system can change through heat (Q) added or removed from the system or work (W) done on or by the system. The first law is expressed as ΔU = Q - W. Specific processes discussed include adiabatic (no heat transfer), isobaric (constant pressure), isochoric (constant volume), and isothermal (constant temperature). Diagrams are used to illustrate these concepts and how to calculate work from changes in pressure and volume.
Thermodynamic notes 2
The first law of thermodynamics states that energy can be transformed from one form to another, but cannot be created or destroyed. It provides a necessary but not sufficient condition for a process to occur. The first law was established through experiments by Joule showing that work input is proportional to heat output. The first law applies to closed systems and describes the various forms energy can take, such as work, heat, internal energy, and how changes in these forms are related through the principle of conservation of energy.
Thermodynamics note chapter:4 First law of Thermodynamics
The document summarizes the first law of thermodynamics. It states that the first law, also known as the law of conservation of energy, provides a basis for relating different forms of energy and their interactions during processes. The first law states that energy cannot be created or destroyed, only changed from one form to another. For closed systems, the total energy change is equal to the net heat transfer minus the net work. For open systems, the energy change also accounts for energy entering or leaving with mass flows. The document provides several examples of applying the first law to common thermodynamic processes.
Availability and irreversibility
(1) Availability analyses determine the maximum work possible from a device given a fuel amount. (2) Available energy is the maximum portion convertible to useful work by ideal processes reducing the system to equilibrium. The remainder is unavailable energy. (3) The theoretical maximum work from a system at state p1, T1 operating with a reservoir at p0, T0 is called availability. (4) Availability accounts for both work against resisting forces and the environment.
What's hot (20)
Lecture 3-4: Exergy, Heating and Cooling, Solar Thermal
Lecture 3-4: Exergy, Heating and Cooling, Solar Thermal
Thermodynamic relations, Clausius Clapreyon equation , joule thomson coefficient
Thermodynamic relations, Clausius Clapreyon equation , joule thomson coefficient
Lecture 14 maxwell-boltzmann distribution. heat capacities
Lecture 14 maxwell-boltzmann distribution. heat capacities
Thermodynamics note chapter:4 First law of Thermodynamics
Thermodynamics note chapter:4 First law of Thermodynamics
Viewers also liked
Consulting cardiologist may reduce the effect of drugs in take
The medications are recommended to diminish mid-section torment so patients whose hearts still contract regularly may feel sufficiently great to build their every day exercises. Presently, new research recommends the inverse is valid.
FINALPublicSpaceinJapan_FINAL_080312
This document catalogs and analyzes different typologies of public space in Japan. It discusses the layered complexity of Tokyo's urban form, with large modern architecture integrated into traditional neighborhoods. Public space takes many forms and scales, from small alleyways to large plazas, shaped by cultural and historical contexts as well as modern development. The document outlines the methodology used during a study abroad program to observe over 50 public spaces across Tokyo and Kyoto based on their functions, scales, dimensions, and other defining elements.
Life Pressure on the mothers
This document presents a study on the life pressures faced by mothers of children with disabilities and how those pressures relate to future anxiety and quality of life. The study examines mothers of children with autism, intellectual disabilities, hearing impairments, and visual impairments. It aims to understand the relationships between life pressures, future anxiety, and quality of life for mothers of children with different disabilities. The study also examines whether there are differences in life pressures, future anxiety, and quality of life between the groups of mothers.
Nasscom Big Data and Analytics Summit 2016: Session III: How Cognitive Comput...
Session III: How Cognitive Computing can Rev Up your Enterprise - A CIO Perspective
Speaker: Sridhar Reddy Donthi
1Karen Torongo BSN
Karen Torongo is a registered nurse seeking a nursing position. She has over 15 years of experience in various nursing roles including public health nurse, home health nurse, clinical manager, documentation specialist, and clinical/floor nurse in settings such as pediatrics, medical/surgical, intensive care, and rapid care. She has a Bachelor's Degree in Nursing from Oakland University and an Associate's Degree in Nursing from Macomb Community College. She is licensed in the state of Michigan.
sajib
MD. Sydur Rahman Sajib is currently working as the head waiter at Ossiano restaurant in Atlantis, The Palm resort in Dubai. He has over 5 years of experience in the hotel industry. Some of his responsibilities as head waiter include managing restaurant operations, ensuring high standards of service and guest satisfaction, supervising and training staff, and achieving sales targets. Previously, he worked as a waiter at The Westin Dhaka in Bangladesh. He holds a Higher Secondary Certificate in Business Studies and has received food and beverage training. He is proficient in English and computer skills.
WomenLead_in_the_Fight_Against_AIDS_CEDPA
Tendayi Westerhof is a model from Zimbabwe who is now an educator working to combat HIV/AIDS and gender inequality. As a child, her father did not support her dreams of furthering her education or career. After becoming pregnant in her youth, she struggled as a single mother but was determined to support her children. Now as a public figure, she speaks candidly about being HIV positive to help reduce stigma and encourage prevention, treatment, and women's empowerment.
AnkitPRao
This document contains the resume of Ankit Pratap Rao summarizing his professional experience and skills. He has over 8 years of experience in product development, application support, and customer relationship management. He is proficient in requirements gathering, system design, development, and troubleshooting. He has worked with various airline companies on projects involving revenue accounting and interline business systems.
Contaminacion
Este documento resume tres resúmenes de casos de estudio sobre conciencia ciudadana y contaminación atmosférica en tres ciudades latinoamericanas: la Ciudad de México, São Paulo y Santiago de Chile. Examina los comportamientos individuales y colectivos, la comunicación social y la participación ciudadana en relación con la contaminación del aire en cada ciudad. Además, analiza los marcos teóricos sobre conciencia ambiental y participación ciudadana, y describe la metodología utilizada en los estudios de caso.
Biftu CV
The document contains a summary of qualifications and experience for Biftu Bogale Alemu. It outlines his educational background which includes a Master's degree in Public Health in Reproductive Health, as well as work experience over 11 years in roles such as a data manager, assistant lecturer, and head of various health centers and offices in Ethiopia. His skills and qualifications include areas related to sustainable development, management, communication, and maternal and child health.
1 búsqueda de información en internet
Los buscadores son sitios que facilitan la búsqueda de información en Internet a través de motores de búsqueda que indexan páginas web y almacenan datos sobre ellas en grandes bases de datos. Los meta buscadores utilizan varios buscadores a la vez para proveer una lista más amplia de resultados. Al ingresar una palabra clave en el cuadro de texto de un buscador, este ejecuta un motor de búsqueda que rastrea la información en la red según los parámetros de cada buscador.
SALC v1 (1)
The document proposes establishing the Sino-American Logistics Council (SALC) to serve as an ongoing platform for cooperation between the US and China on logistics and transportation issues. It would bring together existing initiatives like the Sino-American Logistics Conference under one umbrella organization. SALC would be funded by members and sponsors to facilitate dialogue between industry and government, organize exchanges, and conduct research to strengthen the economic partnership between the two countries. It would have offices and leadership in both the US and China.
"Бессмертный полк" 2-го В класса школы № 135, г. Пермь
Учащиеся 2-го В класса пермской школы № 135 приняли активное участие в акции "Бессмертный полк"
Should your elder with Alzheimer’s live with you?
Your Dad has recently been diagnosed with Alzheimer’s disease. Twice last week you found him on the floor in his home after he had lost his balance. He was confused and had been unable to get up by himself.
3 Reasons Entrepreneurs are Flocking to South Florida to Start Companies
Mark Seyforth names three reasons entrepreneurs are flocking to south Florida to start companies. Visit MarkSeyforth.com to learn more.
PRCS Construction
- Two workers died from asphyxiation and drowning after entering a manhole to spray sealant without proper confined space entry procedures or protections.
- Victim #1 sprayed sealant in the manhole twice and lost consciousness after the second time, falling into water below. Victim #2 then attempted a rescue but also collapsed.
- The incident violated several OSHA standards regarding confined space entry procedures, training, atmospheric monitoring and more. Formal safety programs and rescue equipment were not in place.
Viewers also liked (19)
Consulting cardiologist may reduce the effect of drugs in take
Consulting cardiologist may reduce the effect of drugs in take
Nasscom Big Data and Analytics Summit 2016: Session III: How Cognitive Comput...
Nasscom Big Data and Analytics Summit 2016: Session III: How Cognitive Comput...
"Бессмертный полк" 2-го В класса школы № 135, г. Пермь
"Бессмертный полк" 2-го В класса школы № 135, г. Пермь
3 Reasons Entrepreneurs are Flocking to South Florida to Start Companies
3 Reasons Entrepreneurs are Flocking to South Florida to Start Companies
Similar to Simpleharmonicmotion
Physics_100_chapt_5.ppt
- Work is defined in physics as force multiplied by the distance moved parallel to the force (Work = F x dist∥). No work is done if there is no movement parallel to the force.
- The work-energy theorem states that work done on or by an object equals its change in kinetic energy. It can also be expressed as a conservation of energy principle where the total mechanical energy (potential + kinetic) remains constant.
- Potential energy can take the form of gravitational potential energy (mgh) or spring potential energy (1/2kx^2). Conservative forces simply change the type of energy but total energy is conserved. Dissipative forces like friction convert mechanical energy to heat which cannot be recovered
Physics_100_chapt_5.ppt
- Work is defined in physics as the product of the force applied and the distance moved in the direction of the force. This definition relates work to a change in kinetic energy according to the work-energy theorem.
- The work-energy theorem states that the work done by conservative forces, such as gravity or elastic forces like springs, results in a change in the total mechanical energy of a system (the sum of potential and kinetic energy). This explains how energy is conserved in various situations.
- Energy can be transferred and transformed, but the total quantity of energy remains constant according to the law of conservation of energy. For example, work done by friction results in a change in heat energy rather than a change in mechanical energy
Work, energy and power
1) In an elastic collision between two bodies in one dimension, both linear momentum and kinetic energy are conserved.
2) By applying the laws of conservation of momentum and kinetic energy, equations relating the velocities of the bodies before and after collision can be derived.
3) These equations allow calculating the unknown velocities if the masses of the bodies and their velocities before collision are known.
Simple harmonic motion
1) Simple harmonic motion is the motion of an object where the acceleration is directly proportional to the displacement from the equilibrium position and directed towards the equilibrium.
2) It can be modeled as circular motion where the acceleration towards the center is proportional to the displacement from the center.
3) Simple harmonic oscillators include spring-mass systems and pendulums, where the restoring force is proportional to the displacement.
Power and energy
Here in this presentation, I have tried to input all the basic and simple concept of Power and Energy. It might be helpful for all. Thank you, everybody.
Work,power and energy
1) Work is done when a force causes an object to move through a distance. It is calculated as work = force x distance.
2) There are different types of energy including kinetic energy from motion, potential energy that is stored, and many others from different sources.
3) The law of conservation of energy states that the total energy in an isolated system remains constant, although it can change forms from one to another, such as potential to kinetic energy.
Power Point Presentation ''Work Power Energy"
1) Work is done when a force causes an object to move through a distance. It is calculated as work = force x distance.
2) There are different types of energy including kinetic energy from motion, potential energy that is stored, and many others.
3) The law of conservation of energy states that the total energy in an isolated system remains constant, although it can change forms from one to another, such as potential to kinetic energy.
Elementary modern physics nuclear energy
This document discusses nuclear energy and atomic energy equations. It defines the key equations for nuclear energy as E=Δmc^2, where Δm is the change in mass before and after a reaction and c is the speed of light. It also outlines the key equations for atomic energy, including the energy of radiation, energy of emission, excitation energy, ionization energy, and equations related to the photoelectric effect and quantum theory.
Lecture19
The document discusses the results of an exam in a physics class on elasticity and oscillations. It provides the grade distributions and averages for the exam, along with lecture materials on springs, Hooke's law, simple harmonic motion, and examples of physics problems involving springs and oscillations. Key concepts covered include restoring forces, potential energy in springs, Young's modulus, and the equations of motion for simple harmonic oscillators.
Lecture19
The document discusses the results of an exam in a physics class on elasticity and oscillations. It provides the grade distributions and averages for the exam, along with lecture materials on springs, Hooke's law, simple harmonic motion, and examples of physics problems involving springs and oscillations. Key concepts covered include restoring forces, potential energy in springs, Young's modulus, and the equations of motion for simple harmonic oscillators.
Introduction to oscillations and simple harmonic motion
Physics presentation about Simple Harmonic Motion of Hooke's Law springs and pendulums with derivation of formulas and connections to Uniform Circular Motion.
References include links to illustrative youtube clips and other powerpoints that contributed to this peresentation.
QHO.pptx
The document discusses the classical and quantum mechanical treatment of the simple harmonic oscillator.
Classically, the simple harmonic oscillator exhibits sinusoidal motion with a single resonant frequency, where the restoring force is proportional to displacement from equilibrium. Quantum mechanically, the energy levels of the 1D harmonic oscillator are quantized and equally spaced. The wave functions are solutions of the Schrodinger equation and can be written as products of Hermite polynomials and Gaussian functions. The energy eigenstates of the 1D harmonic oscillator are (n+1/2)ħω, where n is the vibrational quantum number.
Thermodynamics (2013 new edition) copy
Thermodynamics deals with energy transformation between different forms. Some key concepts covered in the document include:
- The first law of thermodynamics states that energy cannot be created or destroyed, only converted from one form to another.
- For a closed system, the heat transfer (Q) equals the change in internal energy (U) plus the work (W) done by the system.
- For an open system, the heat (Q) equals the change in enthalpy (H) of the system plus the sum of kinetic energy (KE), potential energy (PE), and work (W).
- Other concepts defined include systems, surroundings, properties of fluids, phases of substances, forms of energy
Electrostatics123
This document discusses several topics in electrostatics including:
1. Coulomb's law which states that the electrostatic force between two point charges is directly proportional to the product of their magnitudes and inversely proportional to the square of the distance between them.
2. Electric dipoles which have a dipole moment defined as a vector from the negative to positive charge. An external electric field does no work on a dipole but exerts a torque tending to align it with the field.
3. The potential energy of an electric dipole in an external electric field which is minimum when the dipole is aligned with the field.
Work and energy
This document provides information about physics concepts related to work. It defines work using the formula Work = Force x Distance, and explains this definition in examples of Atlas holding up the Earth and a waiter carrying a tray. It then discusses kinetic energy and the work-energy theorem. Examples are provided for work done by gravity over a change in height, gravitational potential energy, conservation of energy, free fall, pendulums, roller coasters, springs, and multiple forces. Power is also defined and examples using kilowatt-hours are given. The document concludes with multiple choice questions testing understanding of these concepts.
7. Springs In Series And Parallel K 1 K
1. The document discusses simple harmonic motion and elasticity. It provides 10 examples solving problems related to springs, pendulums, simple harmonic oscillators, and periodic motion.
2. Key concepts covered include springs in series and parallel, reduced mass of coupled oscillators, conservation of mechanical energy, and using restoring force to determine angular frequency and time period of oscillations.
3. Various examples solve for time periods of physical pendulums, springs, particles oscillating due to gravity, and coupled oscillators. Restoring force and energy methods are applied.
Gas Exercises.pdf
The document discusses the first law of thermodynamics and equations for calculating work, heat transfer, and internal energy change. It then provides 5 exercises:
1. A gas compressed from 3L to 1L at 2 atm pressure with initial temperature of 300K is calculated to have a final temperature of 367.9K.
2. A gas compressed from 5L to 1L at 4 atm constant pressure with initial 400K temperature is found to have a final temperature of 1062.4K.
3. A gas is expanded with calculations to find its final pressure.
4. Work done on a gas compressed at constant temperature is calculated.
5. Final pressure of a gas heated at
physics-of-vibration-and-waves-solutions-pain
1. This document contains solutions to problems from Chapter 1 of the textbook "The Physics of Vibrations and Waves".
2. It provides detailed calculations and explanations for problems related to simple harmonic motion, including determining restoring forces, stiffness, frequencies, and solving differential equations of motion.
3. Examples include a simple pendulum, a mass on a spring, and vibrations of strings, membranes, and gas columns.
Lo
1) The frequency of the box's oscillations is 0.55 Hz, calculated using the spring constant of 30.0 N/m and the mass of 2.5 kg.
2) When the box is 1/3 of the way to the equilibrium position, its speed is 0.1715 m/s. This is calculated using conservation of energy and the initial amplitude, spring constant, and mass.
3) The total energy of the spring-mass system remains constant, being the sum of kinetic and potential energy. This allows calculating the velocity from the displacement using the initial conditions.
SPM Physics Formula List Form4
1. The document defines various physics concepts including units of measurement, kinematics equations, forces and motion, energy, heat, waves, and optics.
2. Prefixes are provided for the standard form of various units including tera, giga, mega, kilo, deci, centi, and milli.
3. Formulas are given for average speed, velocity, acceleration, linear motion, momentum, impulse, work, power, and more.
4. Concepts around pressure, density, buoyancy, heat transfer, the gas laws, refraction, lenses, and telescopes are also summarized.
Similar to Simpleharmonicmotion (20)
Introduction to oscillations and simple harmonic motion
Introduction to oscillations and simple harmonic motion
More from Conferat Conferat
Cellbiologybiolog
This document summarizes the key organelles and their functions in eukaryotic cells. It discusses three main jobs cells must perform: 1) make energy using mitochondria through cellular respiration or chloroplasts through photosynthesis, 2) make proteins using the nucleus, ribosomes, endoplasmic reticulum and Golgi apparatus, and 3) make more cells using the nucleus and centrioles during cell division. Each organelle, including the cell membrane, vacuoles, lysosomes and others, plays an important role in allowing the cell to carry out these essential functions needed for life.
Salts
A salt is formed when all or part of the hydrogen in an acid is replaced by metal or ammonium ions. There are different types of salts including normal salts, acid salts, basic salts, double salts, and complex salts. Salts can be prepared through reactions such as mixing a dilute acid with a metal to form a soluble salt, reacting an alkali with an acid, and mixing solutions containing ions that form an insoluble salt to produce precipitation. Insoluble salts can also be prepared through double decomposition reactions or by directly combining element constituents.
Acids,basesandsalts acids
This document discusses acids and bases. It defines acids as substances that produce hydrogen ions in water and describes strong acids as completely ionizing and weak acids as partially ionizing. It discusses the basicity of acids based on the number of replaceable hydrogen ions. Acids have sour taste, turn litmus red, and are corrosive when concentrated. Acids react with metals and bases. Bases are substances that neutralize acids to form salts and water. The document also discusses alkalis, neutralization, properties of bases, pH scale, calculations involving concentrations and ions, and buffer solutions.
Atomic sructureandbonding
This document discusses atomic structure and bonding. It begins by explaining electron states using notation like 1s, 2p, 3d. The energy of an electron depends on its state and interactions with other electrons. Valence electrons in the outer shell are important for chemical reactivity. Atoms gain, lose, or share electrons to achieve stable noble gas configurations through ionic bonding between metals and nonmetals or covalent bonding between less electronegative elements. The two main types of chemical bonding are ionic, involving transfer of electrons, and covalent, involving sharing of electron pairs.
Calculationsofwaterofcrystallisation
This document provides examples of calculating the percentage of water in hydrated salts and the percentage of water of crystallization. It also shows how to determine the formula of a salt based on the water of crystallization. Specifically, it demonstrates that the percentage of water in MgSO4.5H2O is 42.86% and the percentage of water of crystallization in CuSO4.xH2O is 36%. It further determines that the formula for CuSO4.xH2O is CuSO4.5H2O based on the mole ratio of CuSO4 to H2O being 1:5.
Gaslawsprep
The document summarizes several gas laws:
1) Boyle's law states that the volume of a fixed mass of gas is inversely proportional to its pressure at constant temperature.
2) Charles' law states that the volume of a fixed mass of gas is directly proportional to its absolute temperature if pressure remains constant.
3) Gay-Lussac's law states that the pressure of a fixed mass of gas is directly proportional to its absolute temperature if volume remains constant.
4) The general gas law combines Boyle's, Charles', and Gay-Lussac's laws to relate the pressure, volume, temperature, and amount of gas in a system.
Chemicalcombinationsmoles,molecularandempirical
1) The document discusses concepts related to chemistry including relative atomic mass, relative molecular mass, moles, and empirical and molecular formulae.
2) It provides examples of calculating relative atomic mass, relative molecular mass, moles, percentage composition by mass, and determining empirical and molecular formulae.
3) Key formulas and concepts covered include using the atomic masses of elements to determine relative atomic mass and molecular mass, the definition of a mole in relation to Avogadro's number, and methods for calculating the number of moles and atoms in a sample.
Chemicalcombinationsbalancingchemeqns
The document discusses several laws of chemical combinations and balancing chemical equations. It introduces the law of conservation of mass, law of definite proportions, law of multiple proportions, and law of reciprocal proportions. It also defines valency as the combining power of an element and discusses balancing chemical equations by ensuring the left and right sides match based on atom counts. An example calculation is provided to determine the mass of O2 needed to burn a given mass of sodium.
Separationof mixtures andpurification of chemicalsubstances
This document discusses various techniques for separating mixtures and purifying chemical substances, including sieving, magnetic separation, sublimation, decantation, filtration, centrifugation, evaporation, crystallization, fractional crystallization, precipitation, distillation, fractional distillation, separating funnel, and chromatography. It provides examples of using sublimation to purify iodine and ammonium chloride, centrifugation to separate suspensions by spinning, and crystallization to separate salts that decompose on heating, such as iron(II) tetraoxosulphate(VI)-heptahydrate. Distillation and fractional distillation techniques are also outlined for recovering solvents from solutions and separating miscible liquids like in petroleum industries.
Work,energyandpower
Work is done when a force moves an object through a distance in the direction of the force. Work (W) is equal to the product of the force (F) and distance (s) moved, or W=Fxs. Energy is the capacity to do work and is also measured in joules. The principle of conservation of energy states that in a closed system, the total amount of energy remains constant. Power is the time rate of doing work and is measured in watts. Power is equal to work done divided by the time taken, or W/t.
WavesPREPWALK
A wave is a disturbance that transfers energy through a medium without displacing the medium. There are two types of waves: transverse waves, where the direction of vibration is perpendicular to the direction of travel, and longitudinal waves, where the direction of vibration is parallel. The amplitude of a wave is its maximum displacement from the mean position. Important wave properties include speed, frequency, wavelength, and the equation that describes a traveling wave using variables like amplitude, angular velocity, time, and position. Waves can be progressive, traveling in one direction, or stationary, formed by the combination of two progressive waves traveling in opposite directions. Key wave properties include reflection, refraction, diffraction, polarization, and interference.
Unitsandmeasurements
This document discusses the International System of Units (SI) used to measure physical quantities. It defines fundamental units like length, time and temperature, and derived units obtained by combining fundamental units, like volume. Multiples and submultiples are used to modify units. Dimensional analysis determines if equations are dimensionally correct by examining the dimensions of each term. Various instruments are described for measuring length, time, mass and weight at different scales, including vernier calipers, micrometer screws, stopwatches, balances and more. The key difference between mass and weight is also noted.
Thermalexpansion
Thermal expansion describes how the size of materials changes with increasing temperature. There are three main types of thermal expansion:
1. Linear expansion is the increase in length per unit length for each degree rise in temperature.
2. Area expansion can be calculated from linear expansion.
3. Volume expansion also relates to linear expansion, with volume expansion being three times the linear expansion rate.
Water is an anomaly as it contracts in volume from 0 to 4 degrees C before expanding normally at higher temperatures.
Temperatureanditsmeasurement
This document discusses temperature and its measurement. It defines temperature as a measure of hotness or coldness, while heat is a form of energy that can transfer between bodies with different temperatures. There are several types of thermometers discussed for measuring temperature, including mercury-in-glass, gas, thermoelectric, and resistance thermometers. Gas and resistance thermometers provide the widest measurement ranges, from -270°C to 1500°C and -180°C to 1520°C respectively. The document also provides examples of converting between Celsius, Fahrenheit and Kelvin temperature scales.
Soundwaves
This document summarizes key concepts about sound waves, including:
- The speed of sound varies in different mediums, such as 332 m/s in air, 1500 m/s in water, and up to 500 m/s in steel.
- The Doppler effect describes the change in frequency or pitch of a sound wave emitted by a moving source as it approaches or moves away from an observer.
- For vibrations in closed and open pipes, the fundamental frequency and harmonic frequencies are determined by the length of the pipe based on quarter, half, and three-quarter wave patterns.
- The velocity of a wave propagated along a fixed medium like a string or wire depends on the square root of
Refractionoflight onplanesurfacescurved
This document discusses refraction of light through plane and curved surfaces as well as glass prisms. It defines refractive index as the ratio of the speed of light in one medium to the speed in another. Snell's law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant, known as the refractive index, depending on the optical densities of the two media. Total internal reflection occurs when light passes from a denser to a less dense medium and the incident angle exceeds the critical angle.
Reflection of light at plane or curved surfaces
This document discusses the reflection of light at plane and curved surfaces. It covers the laws of reflection, the formation of images in plane mirrors, reflection using inclined and curved mirrors, and mirror formulas. The two laws of reflection are that the incident ray, reflected ray, and normal all lie in the same plane, and that the angle of incidence equals the angle of reflection. Images in plane mirrors are virtual, upright, and laterally inverted with the same size and distance behind the mirror as the object is in front. Reflection by curved mirrors depends on whether the mirror is convex or concave, with concave mirrors forming real images and convex mirrors forming virtual images.
Projectiles
This document defines a projectile as an object launched into the air under the influence of gravity and air resistance. It describes useful parameters for projectiles like time of flight, maximum height, and range. Formulas are provided for calculating time to maximum height, maximum height, range, and maximum range based on the initial velocity, angle of projection, and gravitational acceleration. The document also explains how to resolve projectile motion into horizontal and vertical components.
Pressure
Pressure is defined as force per unit area. Pressure in liquids is determined by the density of the liquid, height of the liquid column, and acceleration due to gravity. According to Pascal's principle, pressure applied to a confined fluid is transmitted undiminished throughout the fluid and to the walls of its container. Atmospheric pressure is caused by the weight of the air above the earth's surface and decreases with increasing altitude. Simple devices like mercury barometers and aneroid barometers can be used to measure atmospheric pressure.
Newton’s laws of motion
This document summarizes Newton's laws of motion, including:
1) Newton's first law states that an object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force.
2) Newton's second law states that the acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.
3) Newton's third law states that for every action, there is an equal and opposite reaction.
More from Conferat Conferat (20)
Separationof mixtures andpurification of chemicalsubstances
Separationof mixtures andpurification of chemicalsubstances
Recently uploaded
Main Java[All of the Base Concepts}.docx
This is part 1 of my Java Learning Journey. This Contains Custom methods, classes, constructors, packages, multithreading , try- catch block, finally block and more.
ANATOMY AND BIOMECHANICS OF HIP JOINT.pdf
it describes the bony anatomy including the femoral head , acetabulum, labrum . also discusses the capsule , ligaments . muscle that act on the hip joint and the range of motion are outlined. factors affecting hip joint stability and weight transmission through the joint are summarized.
ISO/IEC 27001, ISO/IEC 42001, and GDPR: Best Practices for Implementation and...
Denis is a dynamic and results-driven Chief Information Officer (CIO) with a distinguished career spanning information systems analysis and technical project management. With a proven track record of spearheading the design and delivery of cutting-edge Information Management solutions, he has consistently elevated business operations, streamlined reporting functions, and maximized process efficiency.
Certified as an ISO/IEC 27001: Information Security Management Systems (ISMS) Lead Implementer, Data Protection Officer, and Cyber Risks Analyst, Denis brings a heightened focus on data security, privacy, and cyber resilience to every endeavor.
His expertise extends across a diverse spectrum of reporting, database, and web development applications, underpinned by an exceptional grasp of data storage and virtualization technologies. His proficiency in application testing, database administration, and data cleansing ensures seamless execution of complex projects.
What sets Denis apart is his comprehensive understanding of Business and Systems Analysis technologies, honed through involvement in all phases of the Software Development Lifecycle (SDLC). From meticulous requirements gathering to precise analysis, innovative design, rigorous development, thorough testing, and successful implementation, he has consistently delivered exceptional results.
Throughout his career, he has taken on multifaceted roles, from leading technical project management teams to owning solutions that drive operational excellence. His conscientious and proactive approach is unwavering, whether he is working independently or collaboratively within a team. His ability to connect with colleagues on a personal level underscores his commitment to fostering a harmonious and productive workplace environment.
Date: May 29, 2024
Tags: Information Security, ISO/IEC 27001, ISO/IEC 42001, Artificial Intelligence, GDPR
-------------------------------------------------------------------------------
Find out more about ISO training and certification services
Training: ISO/IEC 27001 Information Security Management System - EN | PECB
ISO/IEC 42001 Artificial Intelligence Management System - EN | PECB
General Data Protection Regulation (GDPR) - Training Courses - EN | PECB
Webinars: https://pecb.com/webinars
Article: https://pecb.com/article
-------------------------------------------------------------------------------
For more information about PECB:
Website: https://pecb.com/
LinkedIn: https://www.linkedin.com/company/pecb/
Facebook: https://www.facebook.com/PECBInternational/
Slideshare: http://www.slideshare.net/PECBCERTIFICATION
clinical examination of hip joint (1).pdf
described clinical examination all orthopeadic conditions .
RHEOLOGY Physical pharmaceutics-II notes for B.pharm 4th sem students
Physical pharmaceutics notes for B.pharm students
বাংলাদেশ অর্থনৈতিক সমীক্ষা (Economic Review) ২০২৪ UJS App.pdf
বাংলাদেশের অর্থনৈতিক সমীক্ষা ২০২৪ [Bangladesh Economic Review 2024 Bangla.pdf] কম্পিউটার , ট্যাব ও স্মার্ট ফোন ভার্সন সহ সম্পূর্ণ বাংলা ই-বুক বা pdf বই " সুচিপত্র ...বুকমার্ক মেনু 🔖 ও হাইপার লিংক মেনু 📝👆 যুক্ত ..
আমাদের সবার জন্য খুব খুব গুরুত্বপূর্ণ একটি বই ..বিসিএস, ব্যাংক, ইউনিভার্সিটি ভর্তি ও যে কোন প্রতিযোগিতা মূলক পরীক্ষার জন্য এর খুব ইম্পরট্যান্ট একটি বিষয় ...তাছাড়া বাংলাদেশের সাম্প্রতিক যে কোন ডাটা বা তথ্য এই বইতে পাবেন ...
তাই একজন নাগরিক হিসাবে এই তথ্য গুলো আপনার জানা প্রয়োজন ...।
বিসিএস ও ব্যাংক এর লিখিত পরীক্ষা ...+এছাড়া মাধ্যমিক ও উচ্চমাধ্যমিকের স্টুডেন্টদের জন্য অনেক কাজে আসবে ...
How to Manage Your Lost Opportunities in Odoo 17 CRM
Odoo 17 CRM allows us to track why we lose sales opportunities with "Lost Reasons." This helps analyze our sales process and identify areas for improvement. Here's how to configure lost reasons in Odoo 17 CRM
What is Digital Literacy? A guest blog from Andy McLaughlin, University of Ab...
What is Digital Literacy? A guest blog from Andy McLaughlin, University of Aberdeen
BÀI TẬP BỔ TRỢ TIẾNG ANH LỚP 9 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2024-2025 - ...
BÀI TẬP BỔ TRỢ TIẾNG ANH LỚP 9 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2024-2025 - ...Nguyen Thanh Tu Collection
https://app.box.com/s/tacvl9ekroe9hqupdnjruiypvm9rdaneLeveraging Generative AI to Drive Nonprofit Innovation
In this webinar, participants learned how to utilize Generative AI to streamline operations and elevate member engagement. Amazon Web Service experts provided a customer specific use cases and dived into low/no-code tools that are quick and easy to deploy through Amazon Web Service (AWS.)
Pollock and Snow "DEIA in the Scholarly Landscape, Session One: Setting Expec...
Pollock and Snow "DEIA in the Scholarly Landscape, Session One: Setting Expec...National Information Standards Organization (NISO)
This presentation was provided by Steph Pollock of The American Psychological Association’s Journals Program, and Damita Snow, of The American Society of Civil Engineers (ASCE), for the initial session of NISO's 2024 Training Series "DEIA in the Scholarly Landscape." Session One: 'Setting Expectations: a DEIA Primer,' was held June 6, 2024.Walmart Business+ and Spark Good for Nonprofits.pdf
"Learn about all the ways Walmart supports nonprofit organizations.
You will hear from Liz Willett, the Head of Nonprofits, and hear about what Walmart is doing to help nonprofits, including Walmart Business and Spark Good. Walmart Business+ is a new offer for nonprofits that offers discounts and also streamlines nonprofits order and expense tracking, saving time and money.
The webinar may also give some examples on how nonprofits can best leverage Walmart Business+.
The event will cover the following::
Walmart Business + (https://business.walmart.com/plus) is a new shopping experience for nonprofits, schools, and local business customers that connects an exclusive online shopping experience to stores. Benefits include free delivery and shipping, a 'Spend Analytics” feature, special discounts, deals and tax-exempt shopping.
Special TechSoup offer for a free 180 days membership, and up to $150 in discounts on eligible orders.
Spark Good (walmart.com/sparkgood) is a charitable platform that enables nonprofits to receive donations directly from customers and associates.
Answers about how you can do more with Walmart!"
BÀI TẬP BỔ TRỢ TIẾNG ANH 8 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2023-2024 (CÓ FI...
BÀI TẬP BỔ TRỢ TIẾNG ANH 8 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2023-2024 (CÓ FI...Nguyen Thanh Tu Collection
https://app.box.com/s/y977uz6bpd3af4qsebv7r9b7s21935vdRecently uploaded (20)
ISO/IEC 27001, ISO/IEC 42001, and GDPR: Best Practices for Implementation and...
ISO/IEC 27001, ISO/IEC 42001, and GDPR: Best Practices for Implementation and...
RHEOLOGY Physical pharmaceutics-II notes for B.pharm 4th sem students
RHEOLOGY Physical pharmaceutics-II notes for B.pharm 4th sem students
বাংলাদেশ অর্থনৈতিক সমীক্ষা (Economic Review) ২০২৪ UJS App.pdf
বাংলাদেশ অর্থনৈতিক সমীক্ষা (Economic Review) ২০২৪ UJS App.pdf
How to Manage Your Lost Opportunities in Odoo 17 CRM
How to Manage Your Lost Opportunities in Odoo 17 CRM
What is Digital Literacy? A guest blog from Andy McLaughlin, University of Ab...
What is Digital Literacy? A guest blog from Andy McLaughlin, University of Ab...
BÀI TẬP BỔ TRỢ TIẾNG ANH LỚP 9 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2024-2025 - ...
BÀI TẬP BỔ TRỢ TIẾNG ANH LỚP 9 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2024-2025 - ...
Leveraging Generative AI to Drive Nonprofit Innovation
Leveraging Generative AI to Drive Nonprofit Innovation
Pollock and Snow "DEIA in the Scholarly Landscape, Session One: Setting Expec...
Pollock and Snow "DEIA in the Scholarly Landscape, Session One: Setting Expec...
Walmart Business+ and Spark Good for Nonprofits.pdf
Walmart Business+ and Spark Good for Nonprofits.pdf
Film vocab for eal 3 students: Australia the movie
Film vocab for eal 3 students: Australia the movie
BÀI TẬP BỔ TRỢ TIẾNG ANH 8 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2023-2024 (CÓ FI...
BÀI TẬP BỔ TRỢ TIẾNG ANH 8 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2023-2024 (CÓ FI...
Simpleharmonicmotion
- 1. PHYSICS SIMPLE HARMONIC MOTION Short revision series
- 2. s θ PP’ K.E = 0 V = 0 P.E = max = mgh P.E = 0 V = max K.E = max =1/2 mv2 h
- 3. Useful formulae Period of a simple pendulum T = 2π √l/g l = lenght of simple pendulum g = acceleration due to gravity T = period Angular velocity ω = θ/t Θ = angle turned by body t = time takken Linear velocity v = rω
- 4. Acceleration of SHM Angular acceleration is the rate of change of angular velocity with time α = a/r a = αr Frequency – number of complete revolutions per min f = 1/T
- 5. Energy of SHM shm θ PP’ K.E = 0 V = 0 P.E = max = mgh P.E = 0 V = max K.E = max =1/2 mv2 h
- 6. In an elastic spring, F =kx; F being the force used to stretch the spring by a distance, and k = force constant Work done = ½ force x displacement x Kx/2 x X = ½ kx Therefore energy in the spring = ½ kx2 The maximum P.E = ½ kx2
- 7. K.E at any instant = ½ mv2 At position of maximum displacement v = 0 therefore K.E = 0 At that point the total energy = K.E + P.E = 0 + ½ kx2 Total energy = ½ kx2
- 8. At equilibrum when K.E is max, P.E = 0 Total energy will be = K.E + P.E = ½ mv2 + 0 = ½ mv2 But at any other positions besides position of maximum displacement and position of equilibrum total energy = KE + PE = ½ mv2 + ½ kx2
- 9. At position P and P’ which is when there is maximum displacement TE = PE + 0 = mgh θ PP’ K.E = 0 V = 0 P.E = max = mgh P.E = 0 V = max K.E = max =1/2 mv2 h
- 10. End