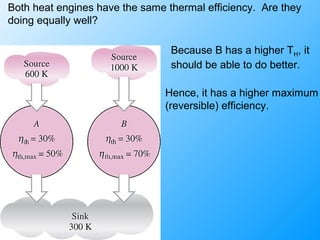
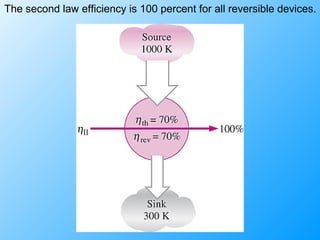
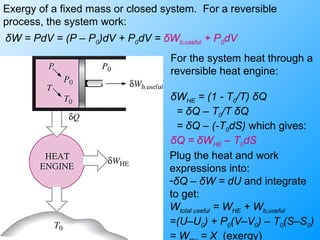
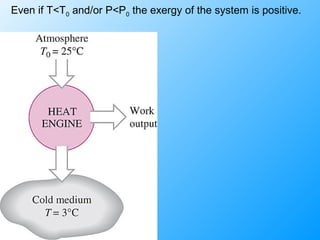
The document discusses second law efficiencies and exergy change of systems. It defines second law efficiency for various devices like heat engines, work-producing devices, refrigerators, and general processes. Second law efficiency compares the actual performance of a device to its theoretical maximum performance under reversible conditions. The exergy change of a closed system depends on the change in internal energy, pressure-volume work, and entropy between initial and final states, accounting for environmental properties. Exergy can represent the useful or recoverable work of a system.

1. Second Law EfficienciesSecond Law Efficiencies
andand
Exergy Change of a SystemExergy Change of a System

2. Both heat engines have the same thermal efficiency. Are they
doing equally well?
Because B has a higher TH, it
should be able to do better.
Hence, it has a higher maximum
(reversible) efficiency.

3. The second law efficiency is a measure of the performance of a
device relative to what its maximum performance could be
(under reversible conditions).
Second law
efficiency for
heat engine A
For heat engine B, ηII = 30%/70% = 43%

4. The second law efficiency is 100 percent for all reversible devices.

5. Second Law EfficienciesSecond Law Efficiencies
• For heat engines =For heat engines = ηηthth//ηηth,revth,rev
• For work - producing devices = WFor work - producing devices = Wuu/W/Wrevrev
• For work – consuming devices = WFor work – consuming devices = Wrevrev/W/Wuu
• For refrigerators and heat pumps =For refrigerators and heat pumps =
COP/COPCOP/COPrevrev
• WWrevrev should be determined using the sameshould be determined using the same
initial and final states as actual.initial and final states as actual.
• And for general processes =And for general processes =
Exergy recovered/Exergy supplied =Exergy recovered/Exergy supplied =
1 – Exergy destroyed/Exergy supplied1 – Exergy destroyed/Exergy supplied

6. Second Law EfficienciesSecond Law Efficiencies
• For explanations of whatFor explanations of what
these terms mean for athese terms mean for a
particular device, see textparticular device, see text
page 401page 401

7. Example 7-6 Second law efficiency of resistance heaters.
Thermal efficiency is 100%. However, COP of a resistance
heater is 1.
What is the COPHP,rev for these conditions? = 1/(1-TL/TH)
It works out to be 26.7
so second law eff. is
COP/COPrev = 1/26.7
or .037 or 3.7%
See now why resistance
heating is so expensive?

8. Exergy of a fixed mass or closed system. For a reversible
process, the system work:
δW = PdV = (P – P0)dV + P0dV = δWb,useful + P0dV
For the system heat through a
reversible heat engine:
δWHE = (1 - T0/T) δQ
= δQ – T0/T δQ
= δQ – (-T0dS) which gives:
δQ = δWHE – T0dS
Plug the heat and work
expressions into:
-δQ – δW = dU and integrate
to get:
Wtotal useful = WHE + Wb,useful
=(U–U0) + P0(V–V0) – T0(S–S0)
= W = X (exergy)

9. Exergy Change of a Closed SystemExergy Change of a Closed System
• ΔΔX = (UX = (U22 - U- U11) + P) + P00(V(V22 - V- V11) – T) – T00(S(S22 - S- S11) + m() + m(۷۷22
22
--
۷۷11
22
) +mg(z) +mg(z22 - z- z11))
• Can also do it on a per-mass basis,Can also do it on a per-mass basis, ΔφΔφ == ΔΔX/m.X/m.
• The exergy change of a system is zero if theThe exergy change of a system is zero if the
state of the system or of the environment doesstate of the system or of the environment does
not changenot change
– Example – steady-flow system.Example – steady-flow system.
• The exergy of a closed system is either positiveThe exergy of a closed system is either positive
or zero.or zero.

10. Even if T<T0 and/or P<P0 the exergy of the system is positive.

11. In flowing systems, you also have flow energy.
The exergy of flow energy is the useful work that would be
delivered by an imaginary piston in the flow (xflow = Pv – P0v.

12. Just like with energy, with
exergy you can replace the
u’s with h’s and get the
exergy of a flowing system.
Just like we use θ for the
energy of a flowing system,
we use the Greek letter psi,
ψ, for the exergy of a flowing
system.

13. Example 7-7 Work Potential of Compressed Air in a Tank.
Assume ideal gas and ke and pe negligible.
Can calculate mass by ideal gas law. Exergy equation:
X1 = m[(u1-u0) + P0(v1-v0) – T0(s1-s0) +V1
2
/2 + gz]
Why? Then use ideal gas law relations and
T1 = T0 to get X1.

14. Exergy Change During a Compression. Change in exergy
equation for flow systems:
Δψ = (h2 – h1) – T0(s2 – s1) + (V2
2
– V1
2
)/2 + g(z2 – z1)
Now, with the two states given, find
h’s and s’s and calculate Δψ.
This represents the minimum work
required to compress the refrigerant
between these two states.
This also represents the maximum
amount of work you can get from
expanding this gas again between
the same two states.