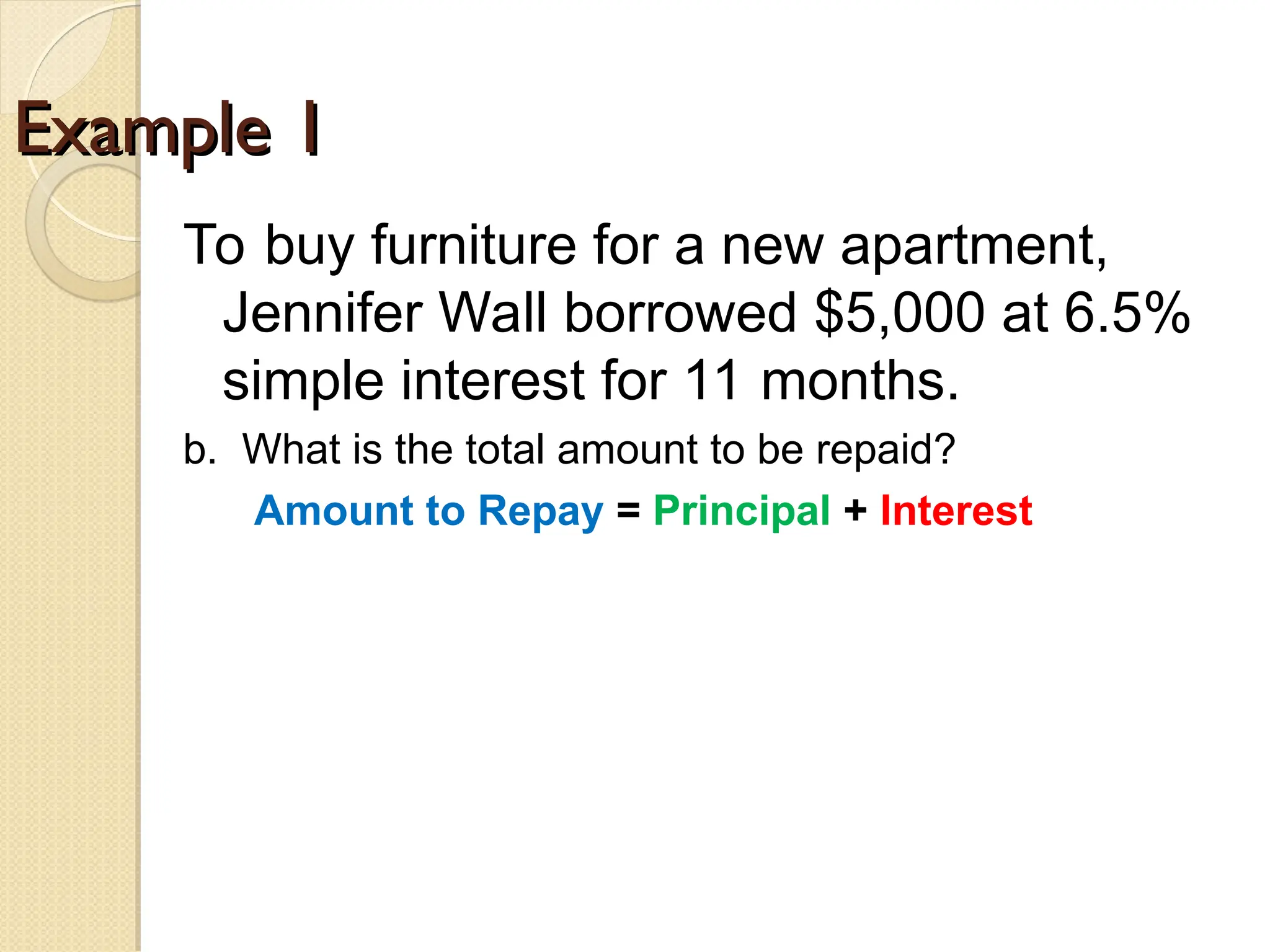
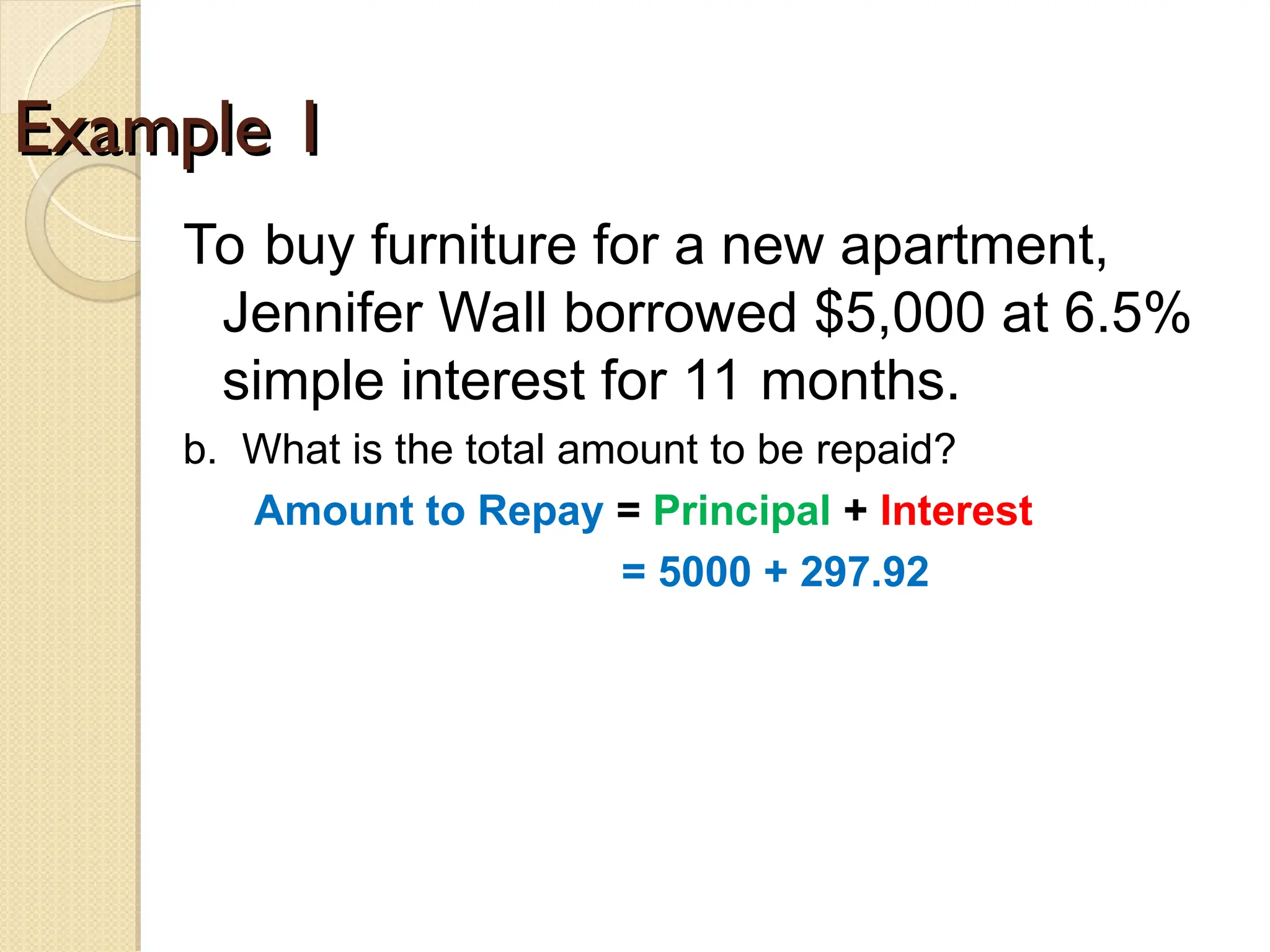
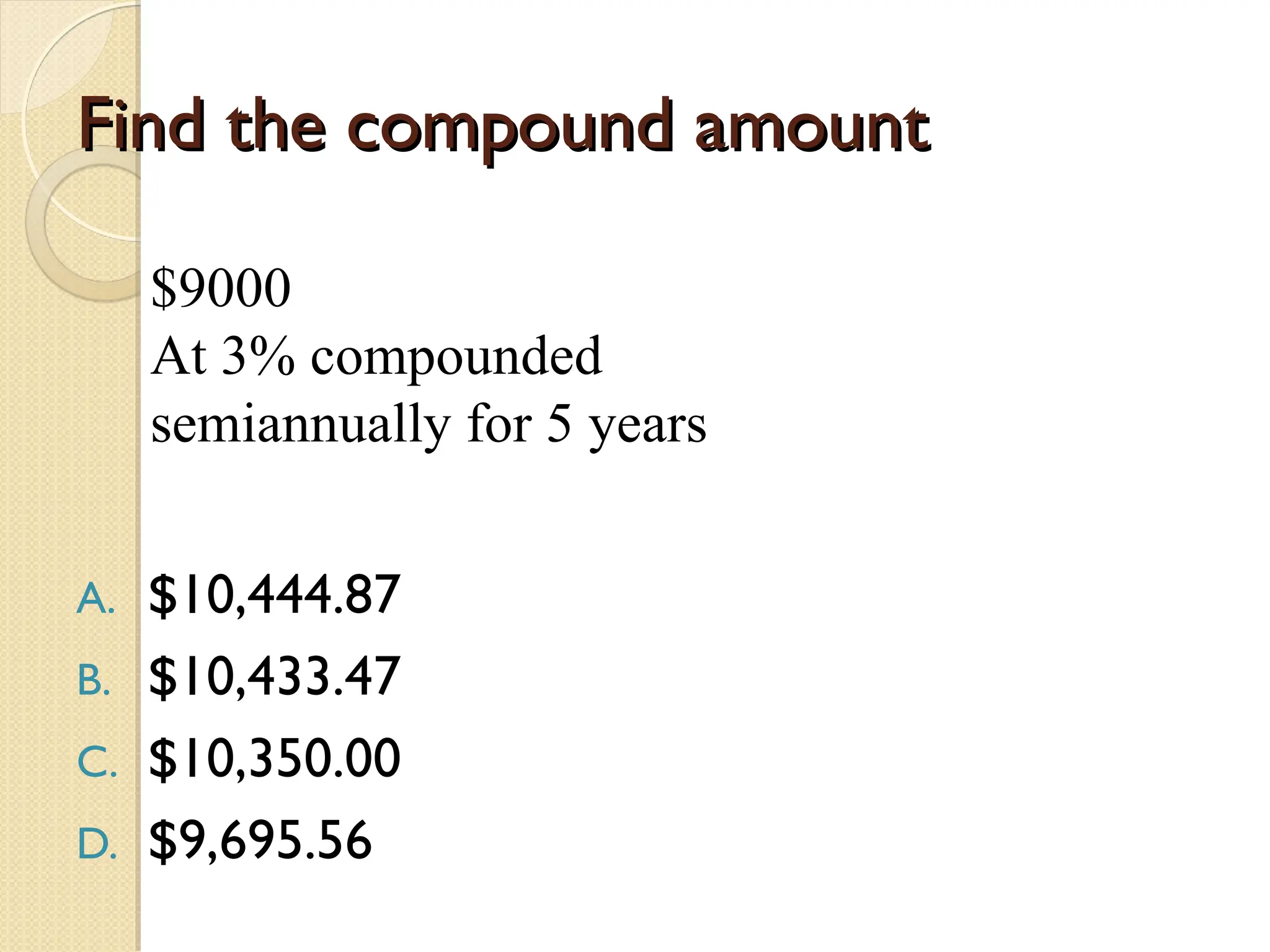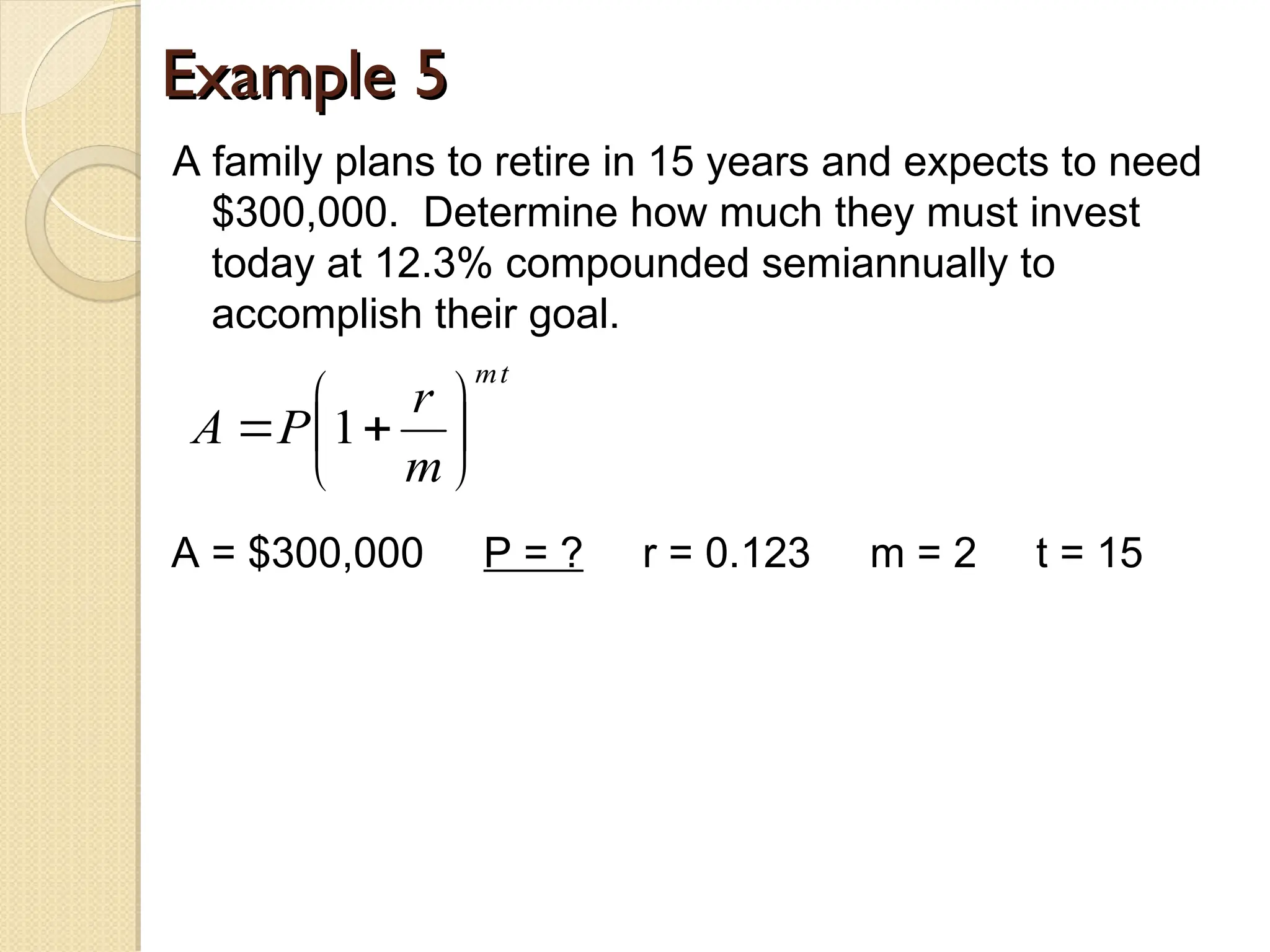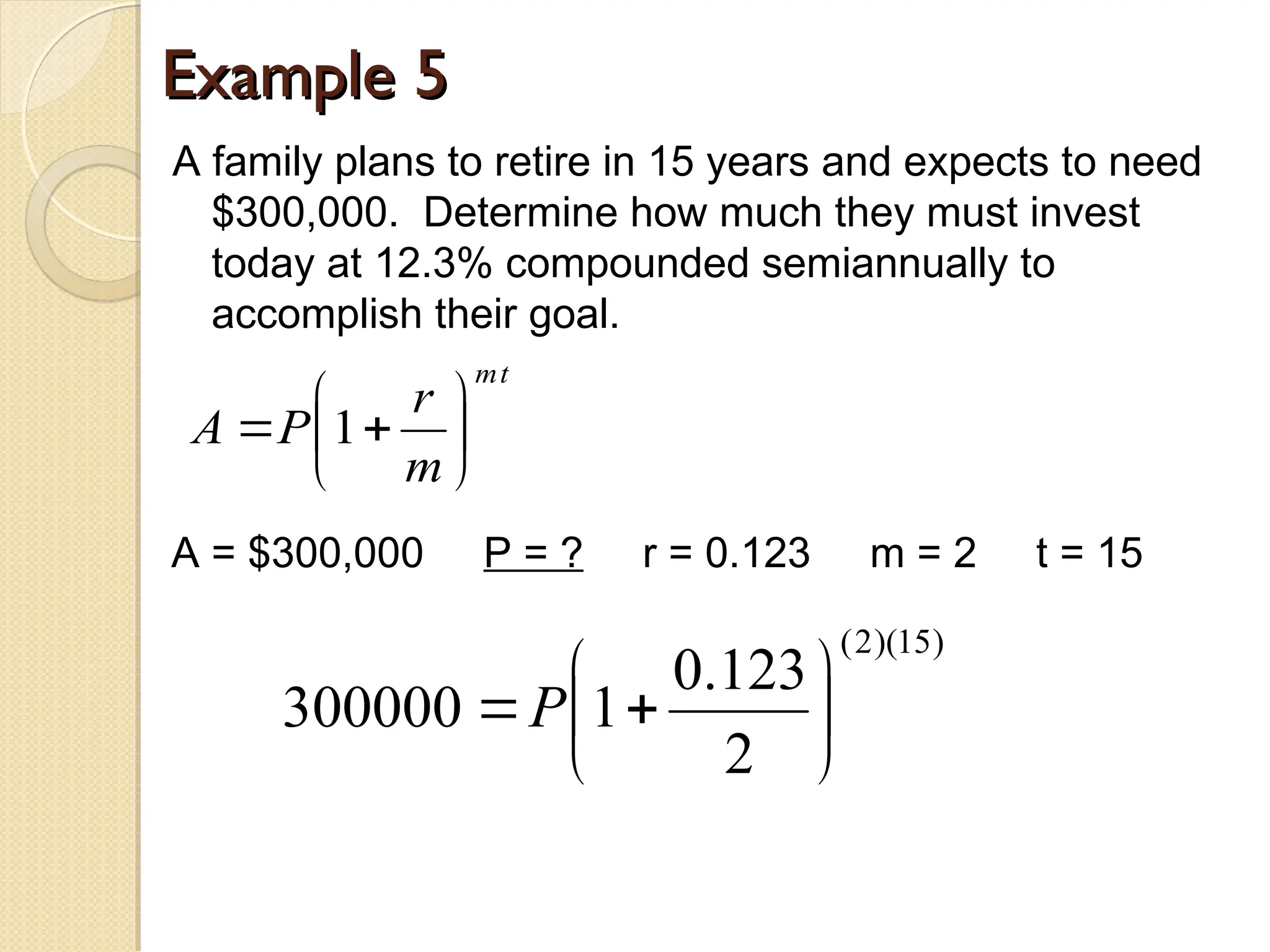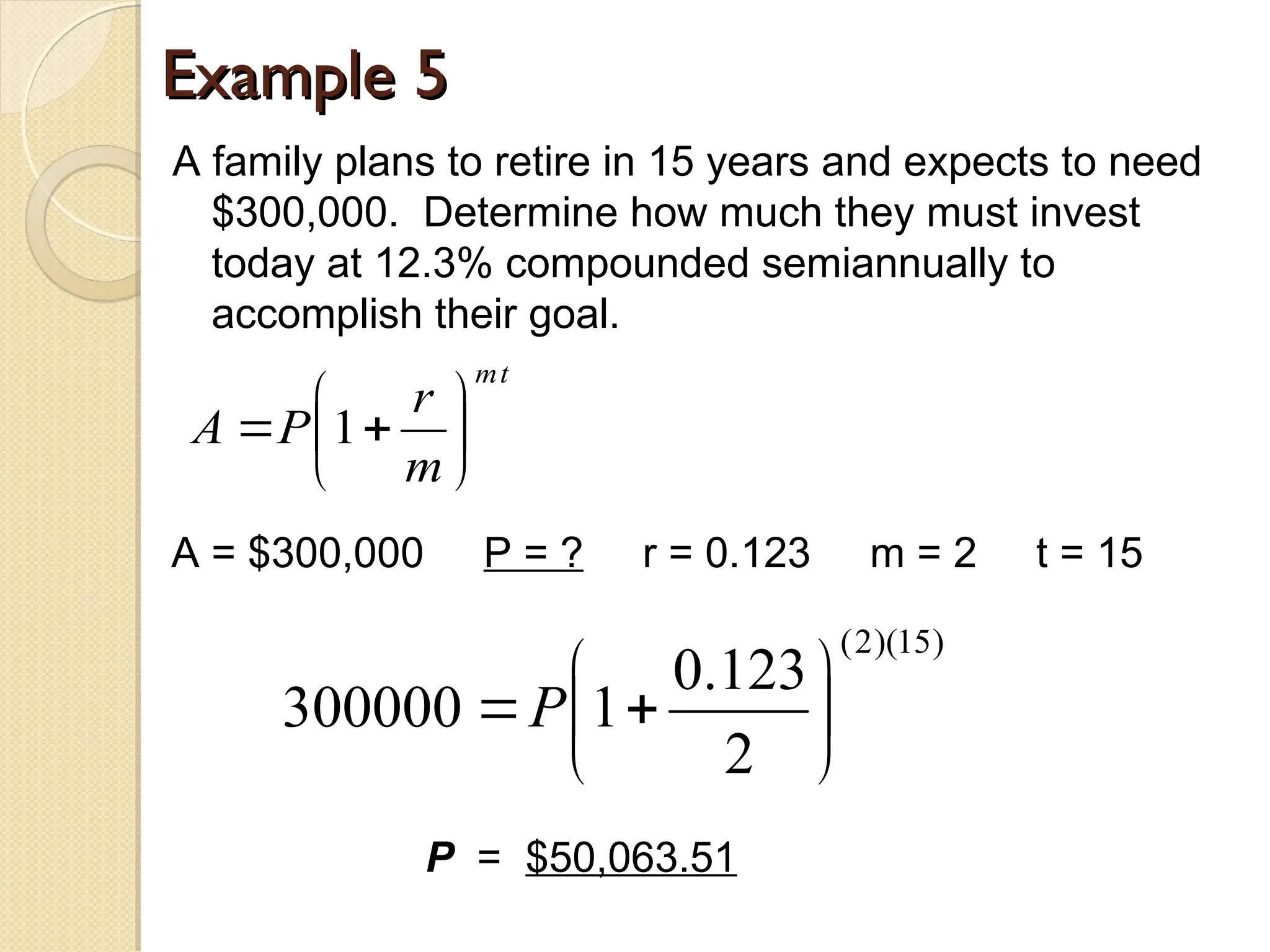The document explains simple and compound interest, detailing their calculations with formulas and examples. It demonstrates how to compute the interest paid on loans and investments, including scenarios of borrowing and savings over specific time periods. Additionally, it outlines the differences between simple interest, where interest is calculated only on the principal, and compound interest, which includes interest that accumulates on previously earned interest.

1. Section 5.1:
Section 5.1:
Simple and Compound Interest
Simple and Compound Interest

2. Simple Interest
Simple Interest
Simple Interest: Used to calculate interest on
loans…often of one year or less.
Formula: I = Prt
 I : interest earned (or owed)
 P : principal invested (or borrowed)
 r : annual interest rate
 t : time in years

3. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at
6.5% simple interest for 11 months.
a. How much interest will she pay?
Simple interest: I = Prt
I = ?

4. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at
6.5% simple interest for 11 months.
a. How much interest will she pay?
Simple interest: I = Prt
I = ? P = $5,000 r = .065 t =11/12

5. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at
6.5% simple interest for 11 months.
a. How much interest will she pay?
Simple interest: I = Prt
I = ? P = $5,000 r = .065 t =11/12
I = Prt = (5000)(0.065)(11/12) =

6. a. How much interest will she pay?
a. How much interest will she pay?
Simple interest:
Simple interest: I
I =
= Prt
Prt
I
I = ?
= ? P
P = $5,000
= $5,000 r
r = .065
= .065 t
t =11/12
=11/12
I
I =
= Prt
Prt = (5000)(0.065)(11/12) = $______
= (5000)(0.065)(11/12) = $______

7. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at
6.5% simple interest for 11 months.
a. How much interest will she pay?
Simple interest: I = Prt
I = ? P = $5,000 r = .065 t =11/12
I = Prt = (5000)(0.065)(11/12) = $297.92

8. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at
6.5% simple interest for 11 months.
b. What is the total amount to be repaid?

9. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at 6.5%
simple interest for 11 months.
b. What is the total amount to be repaid?
Amount to Repay = Principal + Interest

10. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at 6.5%
simple interest for 11 months.
b. What is the total amount to be repaid?
Amount to Repay = Principal + Interest
= 5000 + 297.92

11. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at 6.5%
simple interest for 11 months.
b. What is the total amount to be repaid?
Amount to Repay = Principal + Interest
= 5000 + 297.92 = $ 5,297.92

12. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at 6.5%
simple interest for 11 months.
b. What is the total amount to be repaid?
Amount to Repay = Principal + Interest
= 5000 + 297.92 = $ 5,297.92
Notice here that we really have:
A = P + I … or A = P + Prt = P(1 + rt)

13. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at 6.5%
simple interest for 11 months.
b. What is the total amount to be repaid?
Amount to Repay = Principal + Interest
= 5000 + 297.92 = $ 5,297.92
Notice here that we really have:
A = P + I … or A = P + Prt = P(1 + rt)
So, if you want a direct formula for A with simple interest, use
A = P(1 + rt)

14. Example 1
Example 1
To buy furniture for a new apartment,
Jennifer Wall borrowed $5,000 at 6.5%
simple interest for 11 months.
b. What is the total amount to be repaid?
Amount to Repay = Principal + Interest
= 5000 + 297.92 = $ 5,297.92
Notice here that we really have:
A = P + I … or A = P + Prt = P(1 + rt)
So, if you want a direct formula for A with simple interest, use
A = P(1 + rt)
and, of course if you only want I, then use
I = Prt

15. Find simple interest
Find simple interest
$10,502 at 4.2%
for 10 months
A. $370.66
B. $367.57
C. $404.33
D. $330.81

16. Activity
Activity
Miguel is planning to invest in a local bank.
He wants to earn an extra if 5000 pesos in
interest after 3 years at an annual interest
rate of 4%. How much should he invest to
reach his goal?

17. Activity
Activity
Lara wants to buy a new laptop and decides
to save up through an investment. She
invests 10,000 pesos at 3.5% annual
interest rate. How long will it take for her
investment to generate 4,200 pesos in
interest?

18. Activity
Activity
Carlos borrowed money from his friend to
start a small business. He agreed to pay
back 15,000 pesos after 4 years with 2,700
pesos as interest. What was the annual
interest rate agreed upon?

19. Activity
Activity
Anna invested in a short-term project that
promised 6% annual return. She invested
8,000 pesos for a period of 120 days. How
much will be the exact interest will Anna
earn by the end of the project?

20. Compound Interest
Compound Interest
Compound Interest: more commonly used than simple interest.
With compound interest, the interest itself earns interest.
Formula: t
m
m
r
P
A 






 1

21. Compound Interest
Compound Interest
Compound Interest: more commonly used than simple interest.
With compound interest, the interest itself earns interest.
Formula:
Where
 A is the compound amount (includes principal and interest)
t
m
m
r
P
A 






 1

22. Compound Interest
Compound Interest
Compound Interest: more commonly used than simple interest.
With compound interest, the interest itself earns interest.
Formula:
Where
 A is the compound amount (includes principal and interest)
 P is the initial investment
t
m
m
r
P
A 






 1

23. Compound Interest
Compound Interest
Compound Interest: more commonly used than simple interest.
With compound interest, the interest itself earns interest.
Formula:
Where
 A is the compound amount (includes principal and interest)
 P is the initial investment
 r is the annual percentage rate
t
m
m
r
P
A 






 1

24. Compound Interest
Compound Interest
Compound Interest: more commonly used than simple interest.
With compound interest, the interest itself earns interest.
Formula:
Where
 A is the compound amount (includes principal and interest)
 P is the initial investment
 r is the annual percentage rate
 m is the number of compounding periods per year:
t
m
m
r
P
A 






 1

25. Compound Interest
Compound Interest
Compound Interest: more commonly used than simple interest.
With compound interest, the interest itself earns interest.
Formula:
Where
 A is the compound amount (includes principal and interest)
 P is the initial investment
 r is the annual percentage rate
 m is the number of compounding periods per year:
 Compounded annually, m = 1
 Compounded semiannually, m = 2
 Compounded quarterly, m = 4, etc.
t
m
m
r
P
A 






 1

26. Compound Interest
Compound Interest
Compound Interest: more commonly used than simple interest.
With compound interest, the interest itself earns interest.
Formula:
Where
 A is the compound amount (includes principal and interest)
 P is the initial investment
 r is the annual percentage rate
 m is the number of compounding periods per year:
 Compounded annually, m = 1
 Compounded semiannually, m = 2
 Compounded quarterly, m = 4, etc.
 t is the number of years
t
m
m
r
P
A 






 1

27. Compound Interest
Compound Interest
Compound Interest: more commonly used than simple interest.
With compound interest, the interest itself earns interest.
Formula:
Where
 A is the compound amount (includes principal and interest)
 P is the initial investment
 r is the annual percentage rate
 m is the number of compounding periods per year:
 Compounded annually, m = 1
 Compounded semiannually, m = 2
 Compounded quarterly, m = 4, etc.
 t is the number of years
 n = mt is the total # of compounding periods over all t years
 i = r/m is the interest rate per compounding period
 n
t
m
i
P
m
r
P
A 








 1
1

28. Example 2
Example 2
Suppose that $22,000 is invested at 5.5% interest. Find
the amount of money in the account after 5 years if the
interest is compounded annually.

29. Example 2
Example 2
Suppose that $22,000 is invested at 5.5% interest. Find
the amount of money in the account after 5 years if the
interest is compounded annually.
 n
t
m
i
P
m
r
P
A 








 1
1

30. Example 2
Example 2
Suppose that $22,000 is invested at 5.5% interest. Find
the amount of money in the account after 5 years if the
interest is compounded annually.
A = ?; P = 22,000; r = 0.055; m = 1; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1

31. Example 2
Example 2
Suppose that $22,000 is invested at 5.5% interest. Find
the amount of money in the account after 5 years if the
interest is compounded annually.
A = ?; P = 22,000; r = 0.055; m = 1; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1
)
5
)(
1
(
1
055
.
0
1
22000 







A

32. Example 2
Example 2
Suppose that $22,000 is invested at 5.5% interest. Find
the amount of money in the account after 5 years if the
interest is compounded annually.
A = ?; P = 22,000; r = 0.055; m = 1; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1
12
.
753
,
28
$
1
055
.
0
1
22000
)
5
)(
1
(









A

33. Example 2
Example 2
Suppose that $22,000 is invested at 5.5% interest. Find
the amount of money in the account after 5 years if the
interest is compounded annually.
A = ?; P = 22,000; r = 0.055; m = 1; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1
12
.
753
,
28
$
1
055
.
0
1
22000
)
5
)(
1
(









A
Find the amount of interest earned.

34. Example 2
Example 2
Suppose that $22,000 is invested at 5.5% interest. Find
the amount of money in the account after 5 years if the
interest is compounded annually.
A = ?; P = 22,000; r = 0.055; m = 1; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1
12
.
753
,
28
$
1
055
.
0
1
22000
)
5
)(
1
(









A
Find the amount of interest earned.
Compound Amount (A) = Principal (P) + Interest (I), so
I = A – P

35. Example 2
Example 2
Suppose that $22,000 is invested at 5.5% interest. Find
the amount of money in the account after 5 years if the
interest is compounded annually.
A = ?; P = 22,000; r = 0.055; m = 1; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1
12
.
753
,
28
$
1
055
.
0
1
22000
)
5
)(
1
(









A
Find the amount of interest earned.
Compound Amount (A) = Principal (P) + Interest (I), so
I = A – P
= 28,753.12 – 22,000 = $

36. Example 3
Example 3
If $22,000 is invested at 5.5% interest. Find the amount of
money in the account after 5 years if interest is
compounded monthly. (Round answer to nearest dollar.)

37. Example 3
Example 3
If $22,000 is invested at 5.5% interest. Find the amount of
money in the account after 5 years if interest is
compounded monthly. (Round answer to nearest dollar.)
 n
t
m
i
P
m
r
P
A 








 1
1

38. Example 3
Example 3
If $22,000 is invested at 5.5% interest. Find the amount of
money in the account after 5 years if interest is
compounded monthly. (Round answer to nearest dollar.)
A = ?; P = 22,000; r = 0.055; m = 12; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1

39. Example 3
Example 3
If $22,000 is invested at 5.5% interest. Find the amount of
money in the account after 5 years if interest is
compounded monthly. (Round answer to nearest dollar.)
A = ?; P = 22,000; r = 0.055; m = 12; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1
)
5
)(
12
(
12
055
.
0
1
22000 







A

40. Example 3
Example 3
If $22,000 is invested at 5.5% interest. Find the amount of
money in the account after 5 years if interest is
compounded monthly. (Round answer to nearest dollar.)
A = ?; P = 22,000; r = 0.055; m = 12; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1
945
,
28
$
12
055
.
0
1
22000
)
5
)(
12
(









A
to the nearest DOLLAR

41. Example 3
Example 3
If $22,000 is invested at 5.5% interest. Find the amount of
money in the account after 5 years if interest is
compounded monthly. (Round answer to nearest dollar.)
A = ?; P = 22,000; r = 0.055; m = 12; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1
945
,
28
$
12
055
.
0
1
22000
)
5
)(
12
(









A
to the nearest DOLLAR
Find the amount of interest earned.

42. Example 3
Example 3
If $22,000 is invested at 5.5% interest. Find the amount of
money in the account after 5 years if interest is
compounded monthly. (Round answer to nearest dollar.)
A = ?; P = 22,000; r = 0.055; m = 12; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1
945
,
28
$
12
055
.
0
1
22000
)
5
)(
12
(









A
to the nearest DOLLAR
Find the amount of interest earned.
Compound Amount (A) = Principal (P) + Interest (I), so
I = A – P

43. Example 3
Example 3
If $22,000 is invested at 5.5% interest. Find the amount of
money in the account after 5 years if interest is
compounded monthly. (Round answer to nearest dollar.)
A = ?; P = 22,000; r = 0.055; m = 12; t = 5
 n
t
m
i
P
m
r
P
A 








 1
1
945
,
28
$
12
055
.
0
1
22000
)
5
)(
12
(









A
to the nearest DOLLAR
Find the amount of interest earned.
Compound Amount (A) = Principal (P) + Interest (I), so
I = A – P
= 28,945 – 22,000 = $ 6,945

44. Find the compound amount
Find the compound amount
A. $10,444.87
B. $10,433.47
C. $10,350.00
D. $9,695.56
$9000
At 3% compounded
semiannually for 5 years

45. Example 5
Example 5
A family plans to retire in 15 years and expects to need
$300,000. Determine how much they must invest
today at 12.3% compounded semiannually to
accomplish their goal.

46. Example 5
Example 5
A family plans to retire in 15 years and expects to need
$300,000. Determine how much they must invest
today at 12.3% compounded semiannually to
accomplish their goal.
t
m
m
r
P
A 






 1

47. Example 5
Example 5
A family plans to retire in 15 years and expects to need
$300,000. Determine how much they must invest
today at 12.3% compounded semiannually to
accomplish their goal.
t
m
m
r
P
A 






 1
A = $300,000 P = ? r = 0.123 m = 2 t = 15

48. Example 5
Example 5
A family plans to retire in 15 years and expects to need
$300,000. Determine how much they must invest
today at 12.3% compounded semiannually to
accomplish their goal.
t
m
m
r
P
A 






 1
A = $300,000 P = ? r = 0.123 m = 2 t = 15
)
15
)(
2
(
2
123
.
0
1
300000 






P

49. Example 5
Example 5
A family plans to retire in 15 years and expects to need
$300,000. Determine how much they must invest
today at 12.3% compounded semiannually to
accomplish their goal.
t
m
m
r
P
A 






 1
A = $300,000 P = ? r = 0.123 m = 2 t = 15
P = $50,063.51
)
15
)(
2
(
2
123
.
0
1
300000 






P