Download to read offline
Uploaded byDavid Evans
Asymmetric Key Signatures
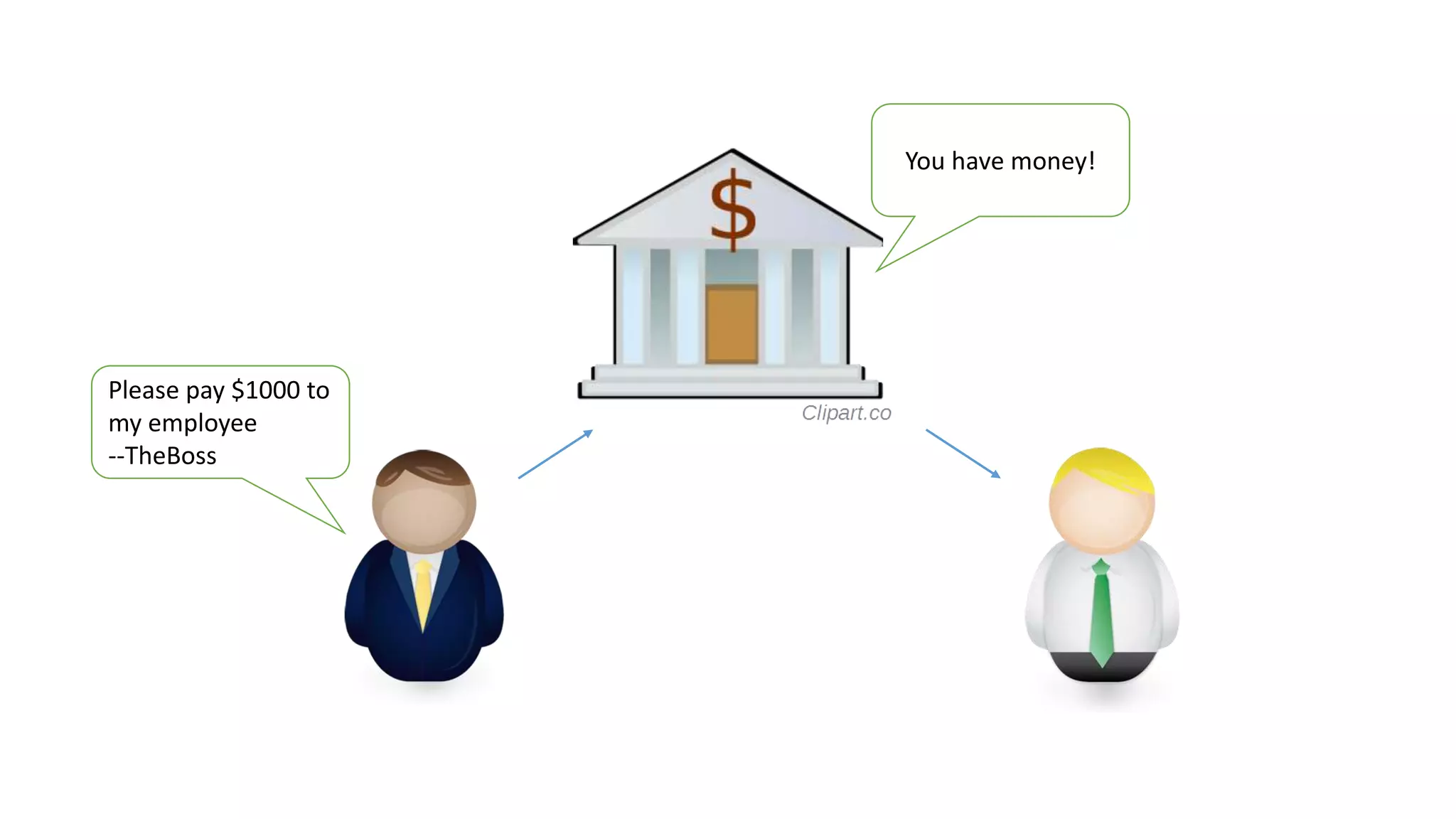
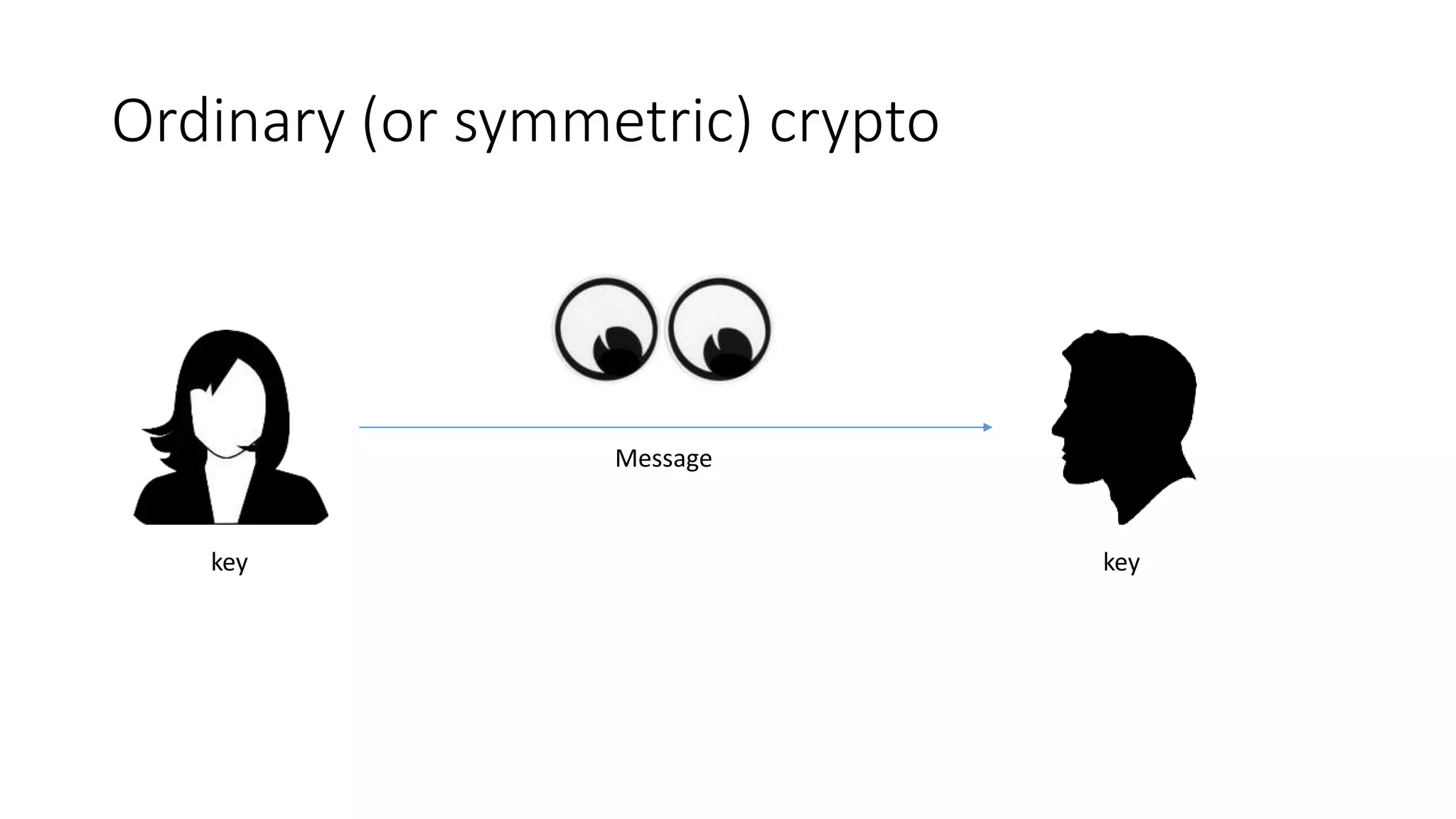
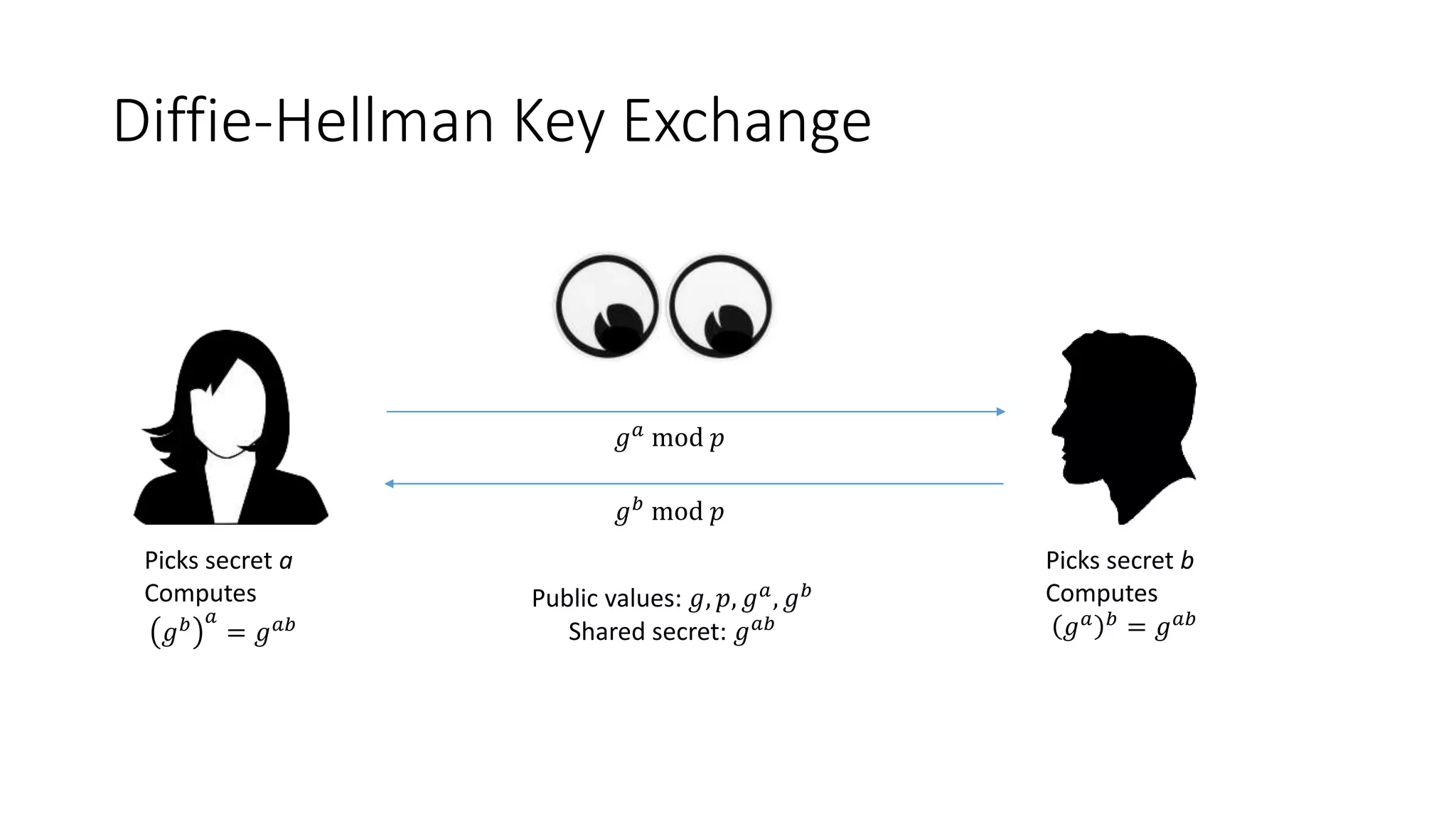
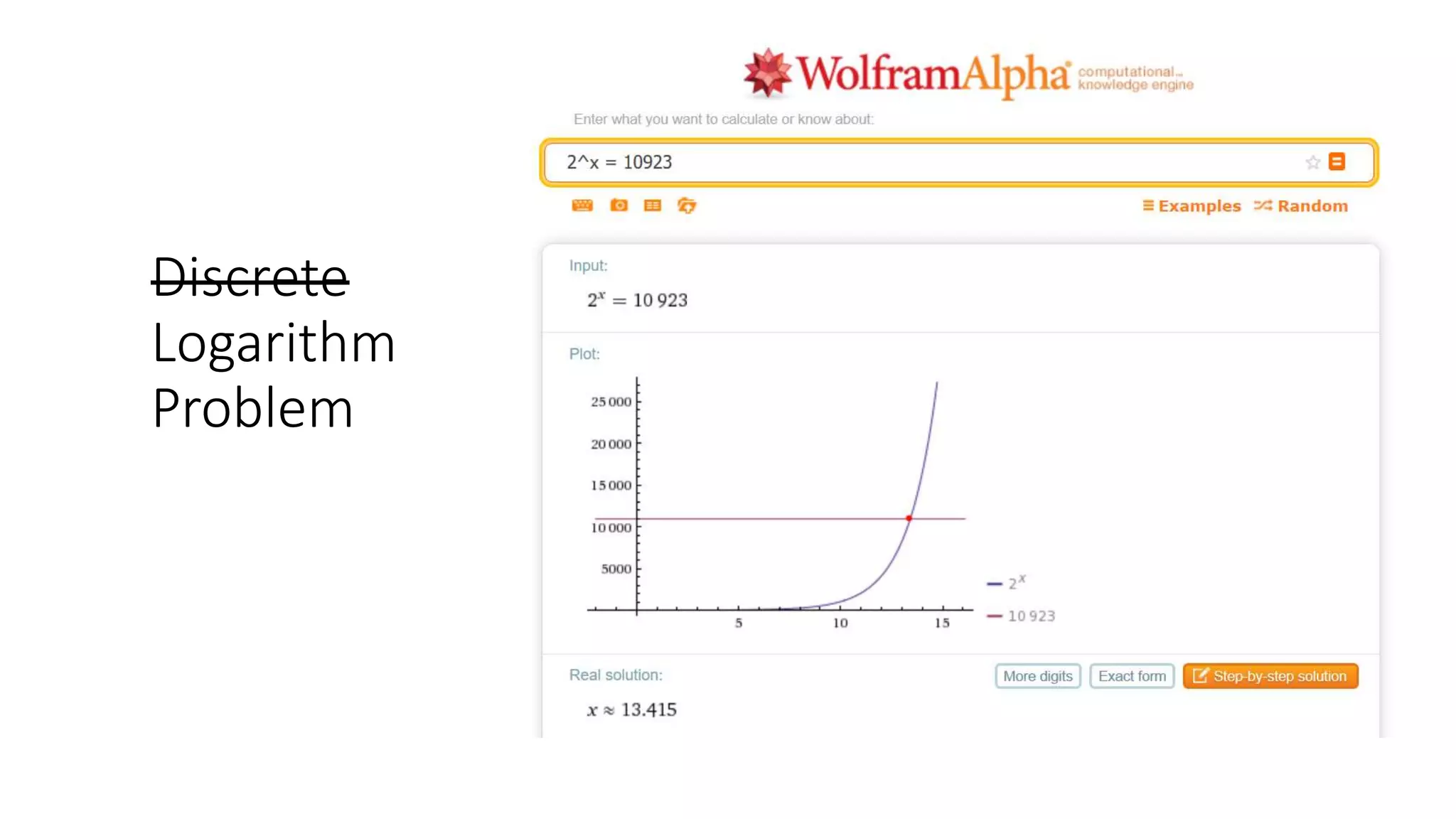
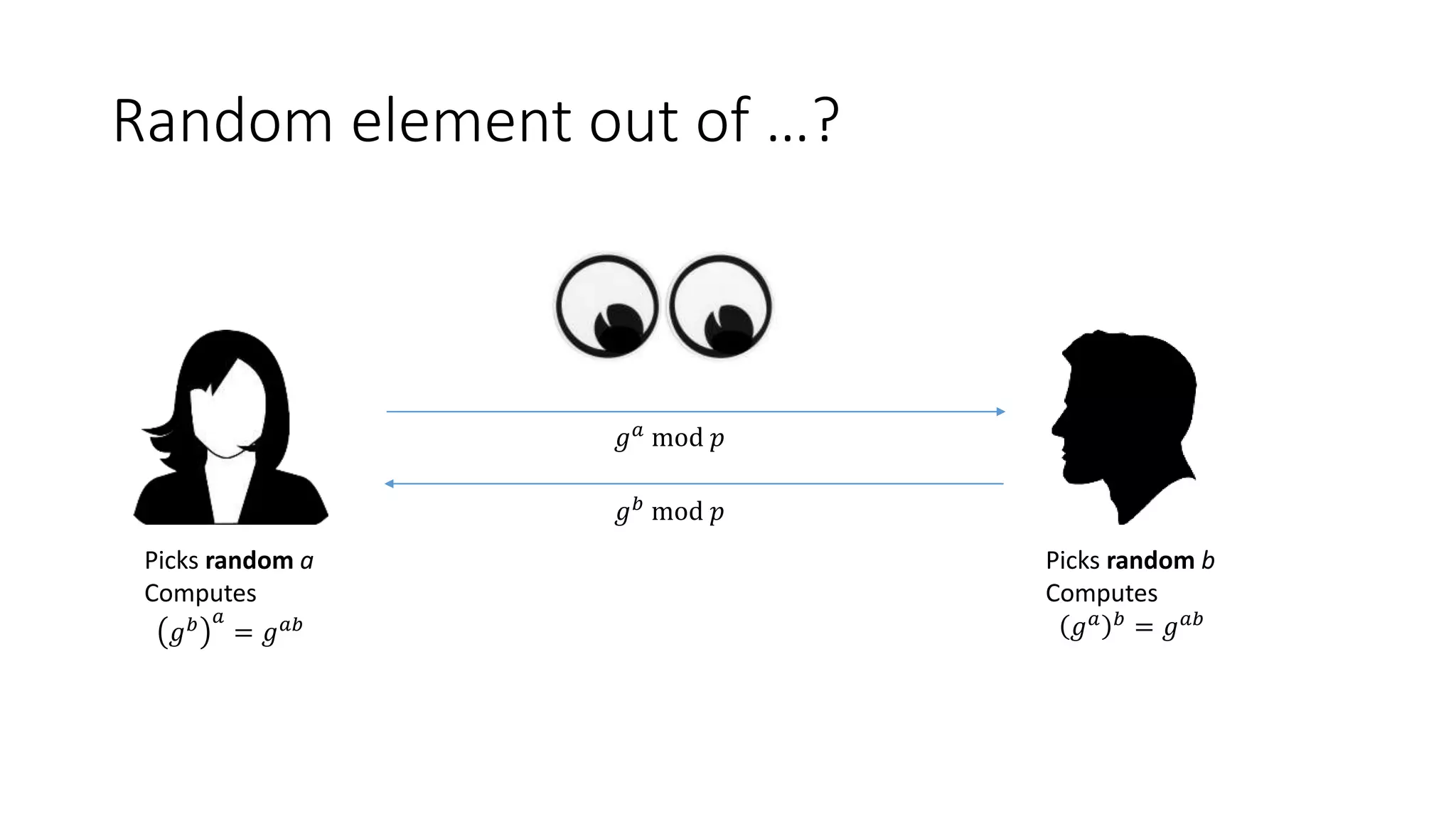
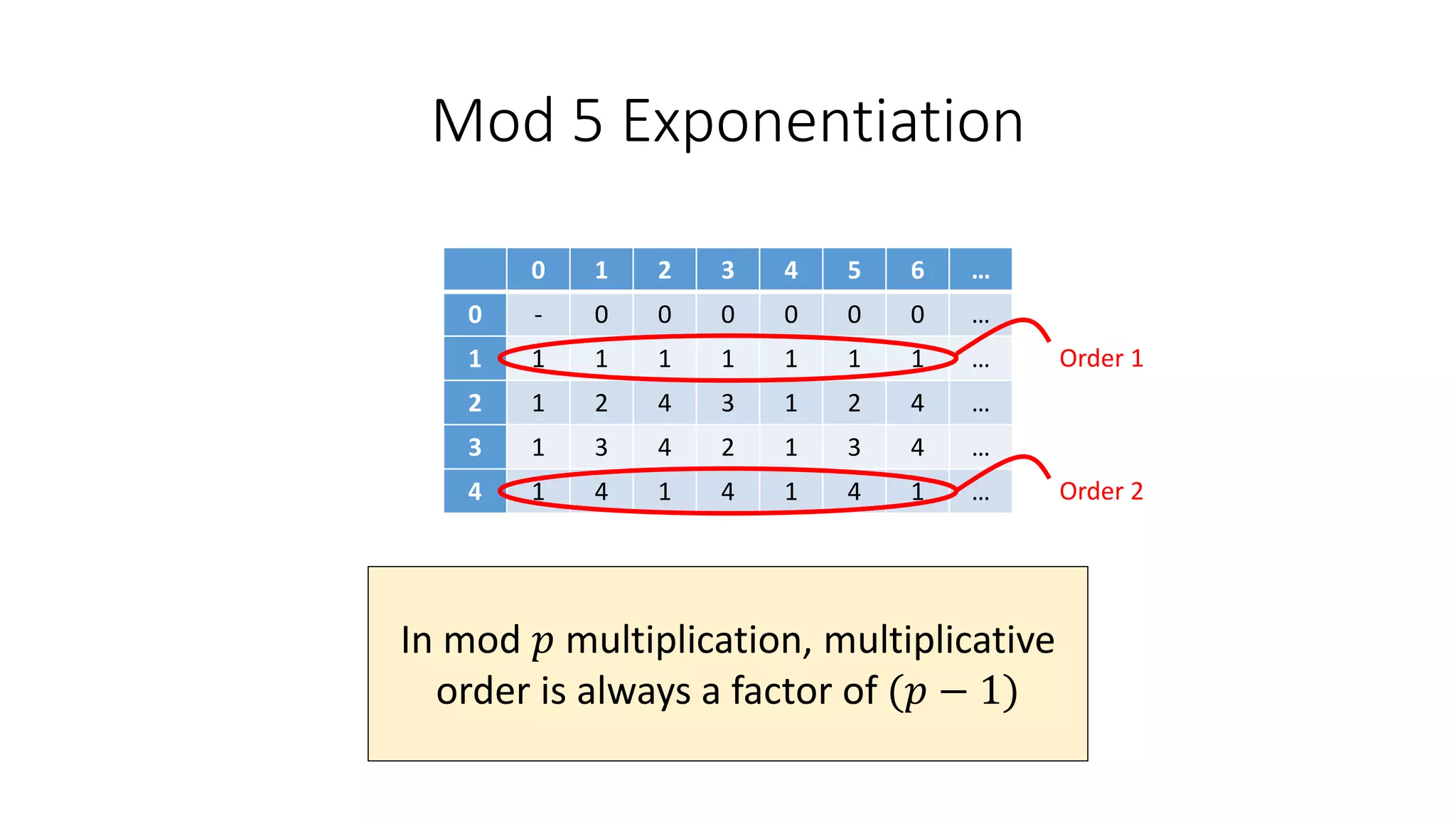
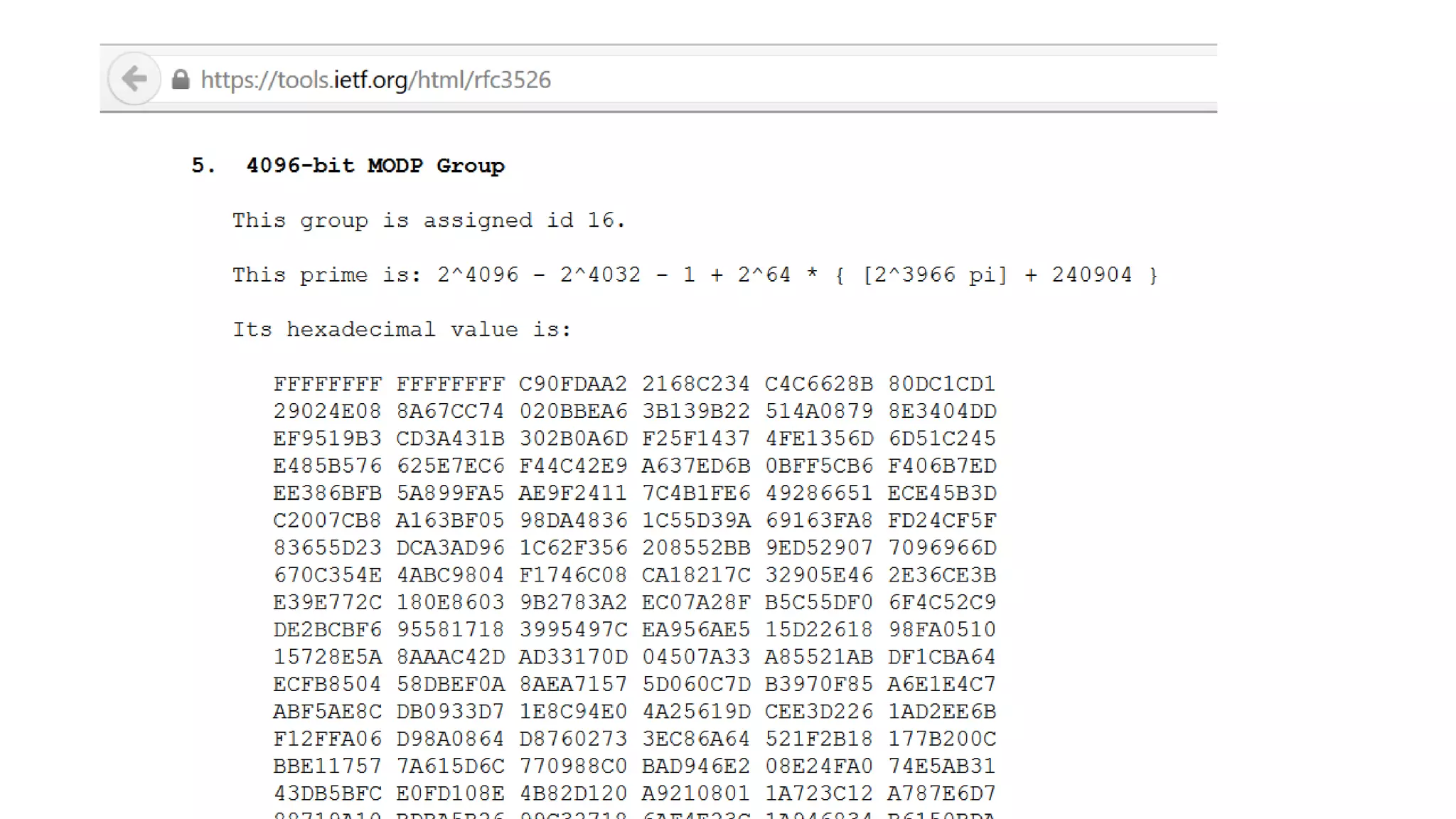
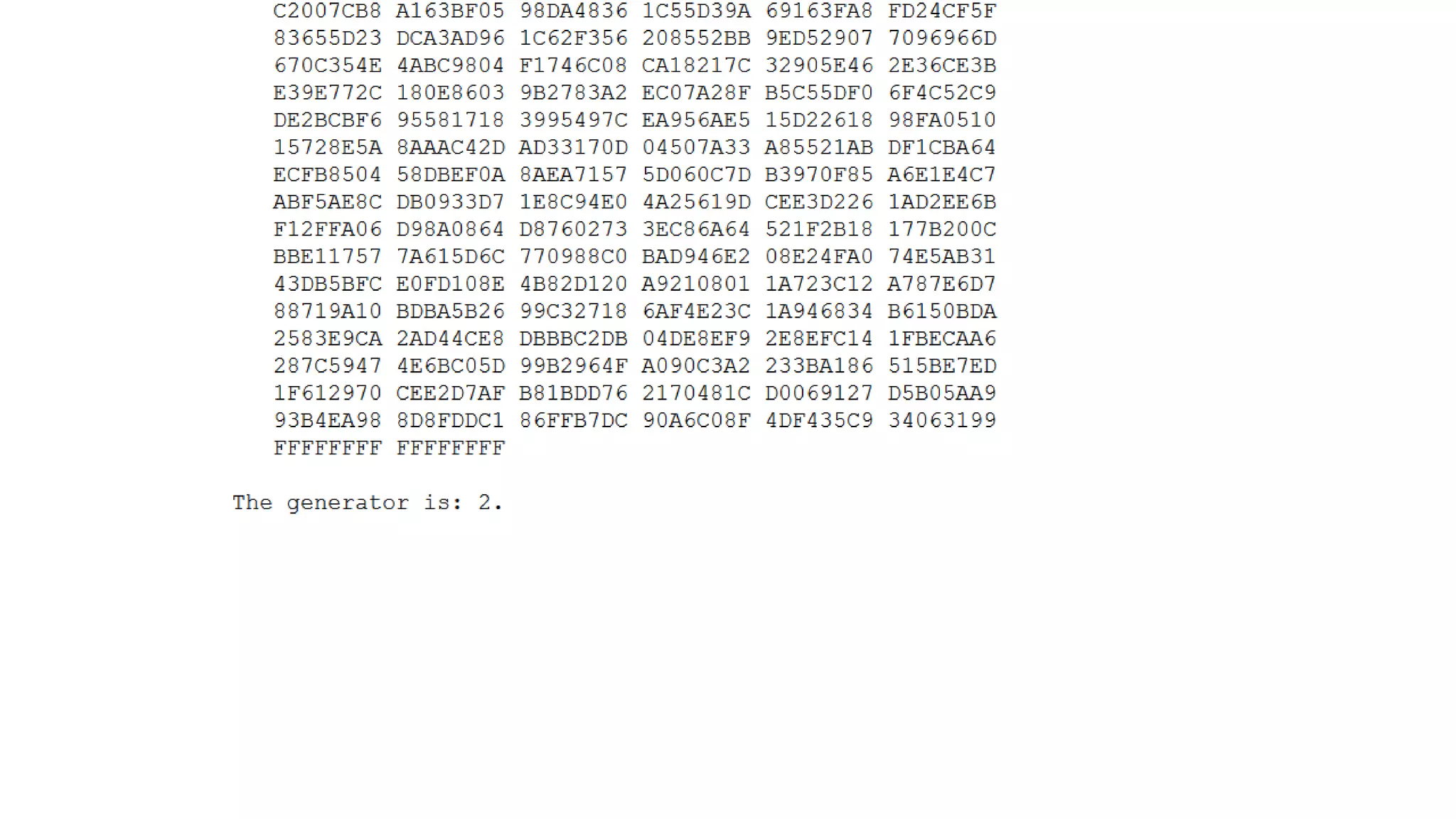
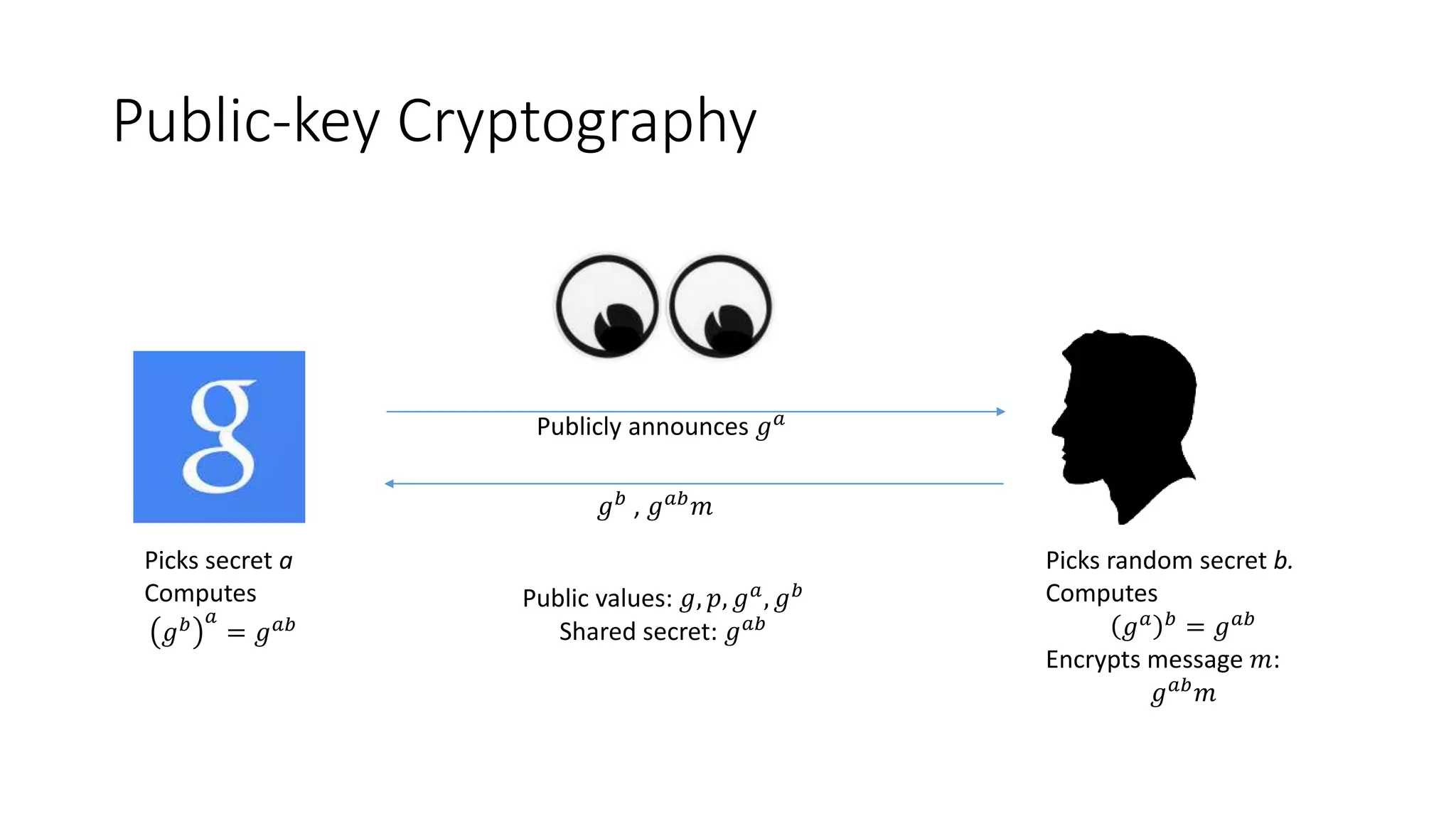
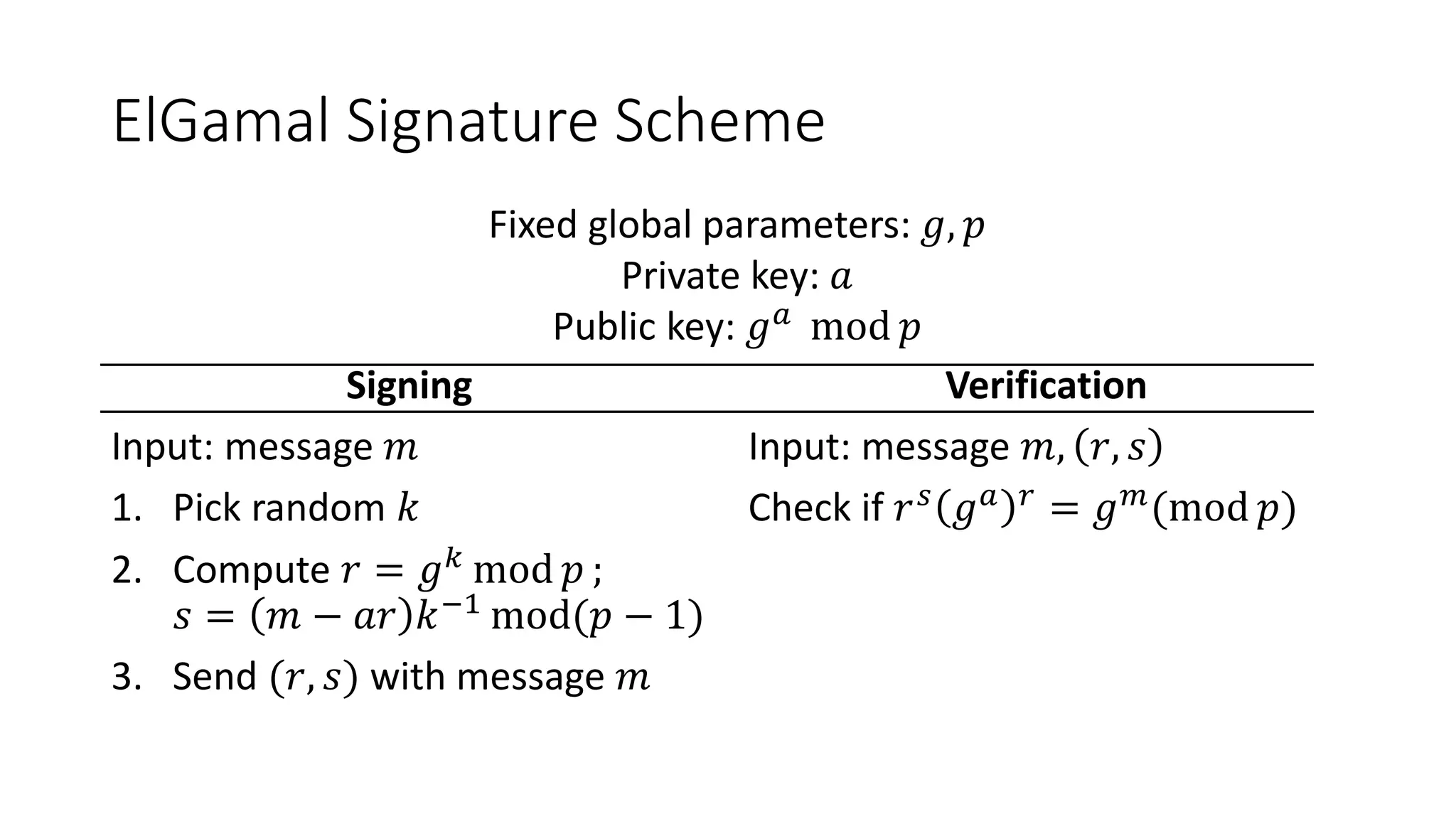
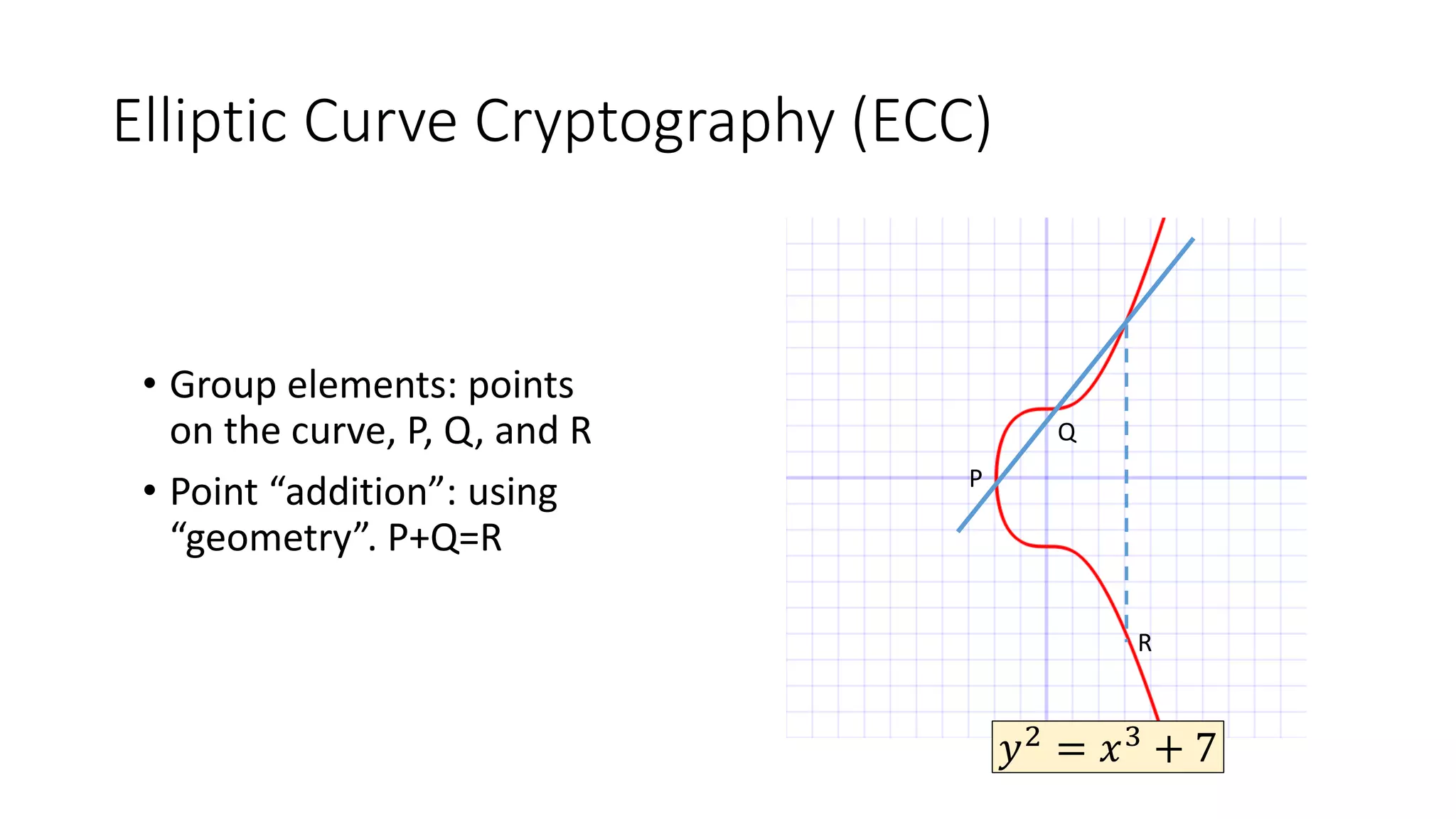
The document covers asymmetric key signatures and cryptographic principles, emphasizing the ease of verification and difficulty of forgery in both digital and ordinary signatures. It describes key concepts such as discrete logarithm problems, public-key cryptography, and elliptic curve cryptography, which are essential for secure digital communications like Bitcoin transactions. The document also touches on specific signature schemes, including ElGamal and ECDSA, illustrating how these cryptographic methods ensure message integrity.
More Related Content
Similar to Asymmetric Key Signatures
![Demystifying Zero Knowledge Proofs [FINAL].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/demystifyingzeroknowledgeproofsfinal-230219182750-7db32511-thumbnail.jpg?width=640&height=640&fit=bounds)
Asymmetric Key Signatures
- 1. Asymmetric Key Signatures DavidEvans and Samee Zahur CS4501, Fall 2015
- 2. Please pay $1000to my employee --TheBoss You have money!
- 3. Real-life Signatures Easy toverify • Bank has your signature Forging unlikely • Legal consequences of forging • Checkbooks are well-guarded • Copying it requires physical access Hard to repudiate • Bank keeps a copy for few months
- 4. Digital Signatures Easy toverify • Everybody has your “verification key”, vk Hard to forge • Nobody but you has the “signing key”, sk Hard to repudiate • Everybody knows only you have signing key 𝑠 = sign 𝑠𝑘 𝑚 true, false = verify 𝑣𝑘(𝑚, 𝑠)
- 5. Topics • Asymmetric cryptography •Digital signatures • Elliptic curve cryptography • Implementation pitfalls
- 6. Ordinary (or symmetric)crypto Message key key
- 7. Whitfield Diffie Martin Hellman NewDirections in Cryptography, 1976
- 8. Diffie-Hellman Key Exchange 𝑔𝑎 mod 𝑝 𝑔 𝑏 mod 𝑝 Picks secret a Computes 𝑔 𝑏 𝑎 = 𝑔 𝑎𝑏 Picks secret b Computes 𝑔 𝑎 𝑏 = 𝑔 𝑎𝑏 Public values: 𝑔, 𝑝, 𝑔 𝑎 , 𝑔 𝑏 Shared secret: 𝑔 𝑎𝑏
- 9. Discrete Logarithm Problem Given𝑔, 𝑦, 𝑝 find 𝑥 such that: 𝑔 𝑥 mod 𝑝 = 𝑦
- 10.
- 11. Random element outof …? 𝑔 𝑎 mod 𝑝 𝑔 𝑏 mod 𝑝 Picks random a Computes 𝑔 𝑏 𝑎 = 𝑔 𝑎𝑏 Picks random b Computes 𝑔 𝑎 𝑏 = 𝑔 𝑎𝑏
- 12. Mod 5 Exponentiation 01 2 3 4 5 6 … 0 - 0 0 0 0 0 0 … 1 1 1 1 1 1 1 1 … 2 1 2 4 3 1 2 4 … 3 1 3 4 2 1 3 4 … 4 1 4 1 4 1 4 1 … Order 1 Order 2 In mod 𝑝 multiplication, multiplicative order is always a factor of (𝑝 − 1)
- 13. Exponent Modulus • Multiplicativeorder 𝑛 is at most 𝑝 − 1 • Pick random 𝑥 such that 0 ≤ 𝑥 < 𝑝 − 1 • 𝑔 𝑎 𝑔 𝑏 mod 𝑝 = 𝑔 𝑎+𝑏 mod 𝑝 = 𝑔 𝑎+𝑏 mod 𝑛 mod 𝑝
- 16. Public-key Cryptography Publicly announces𝑔 𝑎 𝑔 𝑏 , 𝑔 𝑎𝑏 𝑚 Picks secret a Computes 𝑔 𝑏 𝑎 = 𝑔 𝑎𝑏 Picks random secret b. Computes 𝑔 𝑎 𝑏 = 𝑔 𝑎𝑏 Encrypts message 𝑚: 𝑔 𝑎𝑏 𝑚 Public values: 𝑔, 𝑝, 𝑔 𝑎 , 𝑔 𝑏 Shared secret: 𝑔 𝑎𝑏
- 17. Man-in-the-Middle (MITM) 𝑔 𝑎 𝑔𝑏′, 𝑔 𝑎𝑏′ 𝑚 Picks secret a Computes 𝑔 𝑏 𝑎 = 𝑔 𝑎𝑏 Picks secret b. Computes 𝑔 𝑎′ 𝑏 = 𝑔 𝑎′𝑏 Encrypts message 𝑚: 𝑔 𝑎′𝑏 𝑚 𝑔 𝑎′ 𝑔 𝑏, 𝑔 𝑎′𝑏 𝑚 Picks random 𝑎’, 𝑏’, Reads everything
- 18.
- 19. Recall Easy to verify •Everybody has your “verification key”, vk Hard to forge • Nobody but you has the “signing key”, sk Hard to repudiate • Everybody knows only you have signing key 𝑠 = sign 𝑠𝑘 𝑚 true, false = verify 𝑣𝑘(𝑚, 𝑠)
- 20.
- 21. ElGamal Signature Scheme Signing Input:message 𝑚 1. Pick random 𝑘 2. Compute 𝑟 = 𝑔 𝑘 mod 𝑝 ; 𝑠 = 𝑚 − 𝑎𝑟 𝑘−1 mod(𝑝 − 1) 3. Send (𝑟, 𝑠) with message 𝑚 Verification Input: message 𝑚, 𝑟, 𝑠 Check if 𝑟 𝑠 𝑔 𝑎 𝑟 = 𝑔 𝑚(mod 𝑝) Fixed global parameters: 𝑔, 𝑝 Private key: 𝑎 Public key: 𝑔 𝑎 mod 𝑝
- 22. Bitcoin Payment Sign itlike a check!
- 23. Recap 1. We wantto sign transactions digitally on the bitcoin network, such that they are: a) Easy to verify b) Hard to forge c) Hard to repudiate 2. Discrete exponentiation is easy, logarithm is hard 3. We used it to make asymmetric (aka. public) key crypto 4. Same principle used for digital signatures
- 24.
- 26. Informal Requirements Given 𝑔and 𝑦, 𝑔 𝑥 = 𝑦 should be hard to solve for 𝑥
- 27. Group A group isa set of elements (denoted 𝐺) and an associated binary operation (denoted ∗) that satisfies the following: • Closure: 𝑎 ∗ 𝑏 is also a group element, or ∀𝑎, 𝑏: 𝑎 ∗ 𝑏 ∈ 𝐺 • Associativity: ∀𝑎, 𝑏, 𝑐: 𝑎 ∗ 𝑏 ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐) • Identity element: ∃𝑒∀𝑎: 𝑎 ∗ 𝑒 = 𝑎 = 𝑒 ∗ 𝑎 • Inverse: ∀𝑎∃𝑏: 𝑎 ∗ 𝑏 = 𝑒 = 𝑏 ∗ 𝑎 Not necessary, but okay to have: • Commutativity: ∀𝑎, 𝑏: 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
- 28. Additional Cryptographic Properties •Discrete logarithm should be hard • Group operation should be efficient • Implies small key sizes
- 29. Elliptic Curve Cryptography(ECC) • Group elements: points on the curve, P, Q, and R • Point “addition”: using “geometry”. P+Q=R 𝑦2 = 𝑥3 + 7 P Q R
- 30. Elliptic “Curve” Image from:http://www.coindesk.com/math-behind-bitcoin/
- 31. Elliptic Curve DigitalSignature Algorithm (ECDSA) ElGamal Signature Inputs: message 𝑚, private key 𝑎 1. Pick random 𝑘 2. Compute a) 𝑟 = 𝑔 𝑘 mod 𝑝 b) 𝑠 = 𝑚 − 𝑎𝑟 𝑘−1 mod 𝑛 3. Send 𝑟, 𝑠 with message 𝑚 Verification Check if 𝑟 𝑠 𝑔 𝑎 𝑟 = 𝑔 𝑚 ECDSA Inputs: message , private key 1. Pick random k 2. Compute a) , let 3. Send with message Verification If , check
- 34. Please pay $1000to my employee --TheBoss You have money! Jason Benjamin
- 35. Logistics • Next class:hash functions and Bitcoin consensus • Checkup 1 on Monday. Includes everything till today