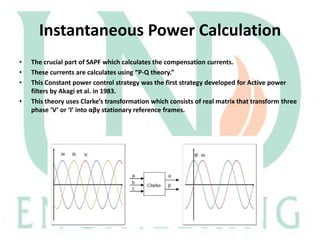
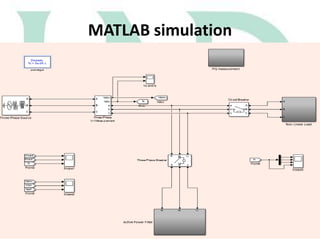
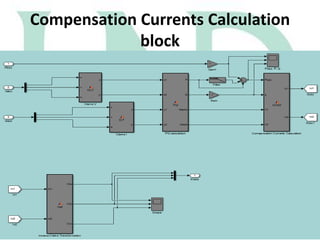
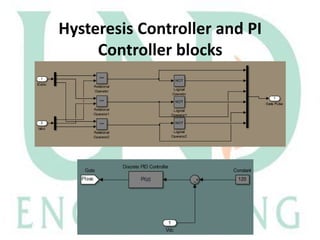
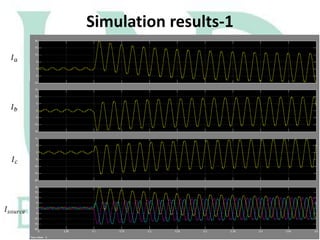
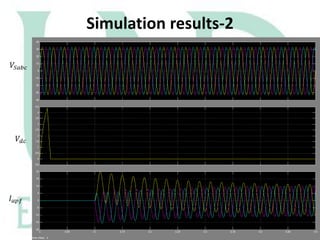
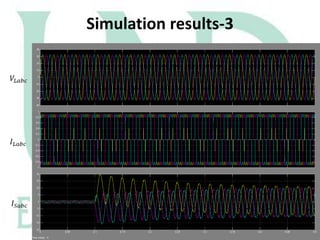
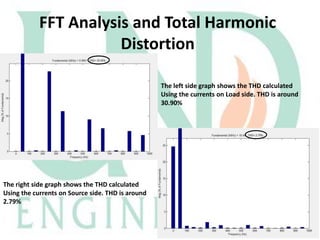
The document describes a Simulink model that was created to improve total harmonic distortion (THD) using a shunt active power filter. The model simulates a power system with a non-linear load connected to an ideal grid voltage. The shunt active power filter is connected 0.1 seconds after simulation start and works to compensate for harmonics by producing currents equal in magnitude but opposite in phase to the load harmonics. Simulation results show the THD is reduced from around 30.9% on the load side to 2.79% on the source side once the active filter is connected, below the maximum allowable limit.

1. A Simulink Model to Improve Total Harmonic
Distortion (THD) using Shunt Active Power
Filter
By,
Ranganath Vallakati
Master of Science in Electrical
Engineering
University of North Dakota

2. Introduction
• Loads: Types of Loads
1. Linear loads – sinusoidal current with sinusoidal voltage
2. Non-linear loads – non-sinusoidal current with sinusoidal voltage
• Harmonics and it’s effects
1. Overheating
2. Voltage distortion and flickering
3. Interference
• Different solutions:
1. Capacitors
2. Compensators
3. Passive filters
4. Active filters

3. Filters
• Active power filter
1.
I.
II.
Series active power filter
SeAPF is connected in series with the T.L
Acts as a controlled voltage source
2.
I.
II.
Shunt active power filter:
ShAPF is connected in parallel with the T.L
Acts as a controlled current source
3. Unified power quality controller
I.
Combination of passive, series and shunt active filters

4. Shunt active power filter
•
The principle of the shunt filter is to produce harmonic currents equal in magnitude but
opposite in-phase to those harmonics that are present in the grid.
•
Phase shift of the harmonic current is 180 degrees.
•
Non-linear load with SAPF becomes a Linear load.
•
SAPF is a closed loop structure
•
•
SAPF can compensate reactive power and can also
mitigate harmonics and distortions.
I(comp) = I(load) - I(source)

5. Shunt Active Power Filter
Reference [1]

6. Different blocks in SAPF
• PWM Converter
• Instantaneous power calculation block
• Reference currents calculation block
• DC voltage regulator

7. PWM Converter
1.
Responsible for power processing.
2.
Consists of VSC or CSC
3.
To force the PWM converter act as a controlled voltage or current source.
4.
VSC is made up of PE devices(GTO, IGBT…)
5.
PE devices are fired based on the APF currents.
6.
APF currents can be calculated using Hysteresis Controller method.

8. Hysteresis Controller
•
The method of controlling a VSC in such a way that the output current will be generated
based on reference current values.
•
A reference value is kept and is compared with the two input of the controller.
•
Based on the error between the 2 inputs and the reference value, signals are generated.
• Inputs to the controller can be taken in two different ways:
1. Direct control method.
2. Indirect control method.

9. Instantaneous Power Calculation
•
•
•
•
The crucial part of SAPF which calculates the compensation currents.
These currents are calculates using “P-Q theory.”
This Constant power control strategy was the first strategy developed for Active power
filters by Akagi et al. in 1983.
This theory uses Clarke’s transformation which consists of real matrix that transform three
phase ‘V’ or ‘I’ into αβγ stationary reference frames.

10. Clarke’s Transformation and It’s
Inverse
•
For a 3-phase system without a neutral/ground, we can neglect the zero sequence
component to make the matrices as

11. Cont.…

12. Average and Oscillating components

13. Actual
Implementation of
p-q Theory in SAPF
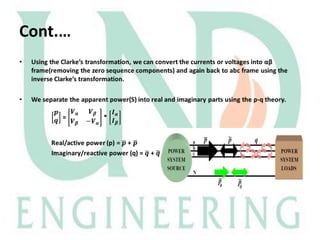
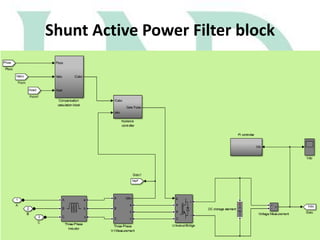
These currents
and voltages are
taken as inputs to
the filter from
the line or load.
The powers to be
compensated are given
input. The compensator
should draw exactly the
given amount of current
that produces the inverse
of powers that are drawn
by the load.
Through
transformation,
we get the real
and imaginary
power values
By applying Inverse
Clarke's
transformation, we get
the actual abc
coordinates which can
be applied to the line
again.
Reference [1]

15. Simulation
Ideal grid voltage V
40 V
Grid frequency f
50 Hz
Grid resistance R
3 mΩ
Grid Inductance I
0.1 μH
DC Capacitor(SAPF)
3.5 μF
Constant DC voltage
120 V
DC Load1 Resistance
60Ω
DC Load1 Inductance
10 mΩ
DC Load2 Resistances
2Ω,4Ω, 6Ω
Simulation time
0.5 seconds
SAPF connection time
0.1 seconds

16. MATLAB simulation

17. Shunt Active Power Filter block

18. Compensation Currents Calculation
block

19. Hysteresis Controller and PI
Controller blocks

20. Simulation results-1

21. Simulation results-2

22. Simulation results-3

23. FFT Analysis and Total Harmonic
Distortion
The left side graph shows the THD calculated
Using the currents on Load side. THD is around
30.90%
The right side graph shows the THD calculated
Using the currents on Source side. THD is around
2.79%

24. Conclusion
•
From our MATLAB/SIMULINK simulation process, we have designed a power system which
consists of source, non-linear load and SAPF which is connected to the actual transmission
line after 0.1 seconds.
•
The initial peaks in the THD are during the time period when the SAPF has not been
connected to the power systems.
•
The maximum allowable limit of Total Harmonic Distortion as per IEEE 519_1992 regulations
is below 5% for bus voltages less than 69KV
•
Using our Shunt Active Power Filter, we have reduced the THD remarkably from 30% to
2.79% on the simulated power systems circuit.

25. References
*1+. “Instantaneous Power Theory and Applications to Power Conditioning” by Hirofumi
Akagi, Edson Hirokazu Watanabe and Mauricio Aredes.
[2]. MATLAB and Simulink R2013b (www.mathworks.com)
[3]. H. Akagi, Y. Kanazawa and A. Nabae, “Generalized Theory of Instantaneous Reactive Power
and It’s Applications,” Transactions of the IEE-Japan, Part B, vol. 103, no.7, 1983
[4]. E. Clarke, Circuit Analysis of A-C Power Systems, Vol.1—Symmetrical and Related
Components, Wiler, 1943.
[5]. SimiPowerSystem, for use with Simulink, by MATLAB

26. Thank You…
• Questions…?
• Comments…?