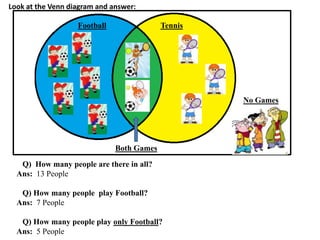
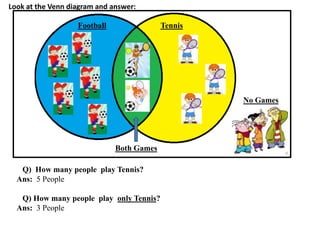
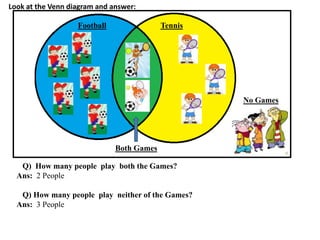
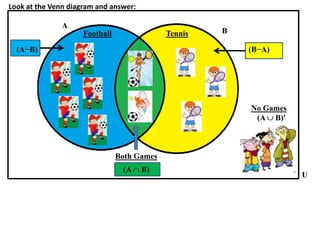
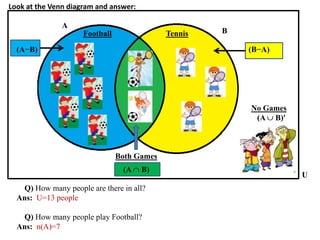
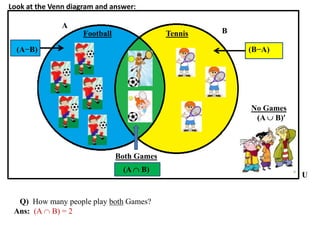
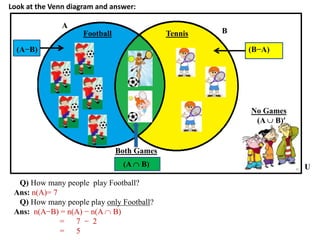
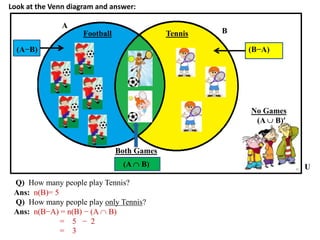
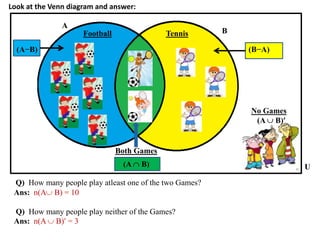
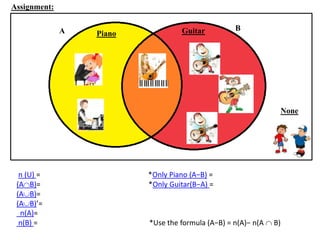
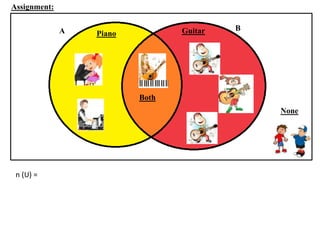
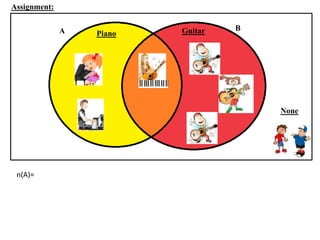
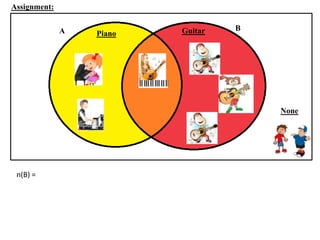
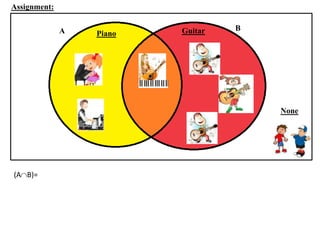
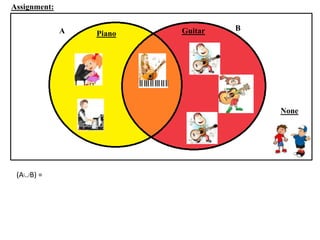
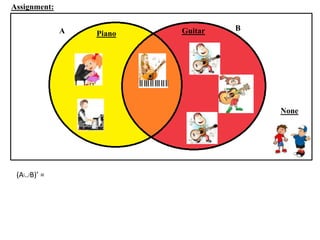
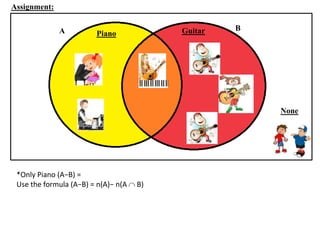
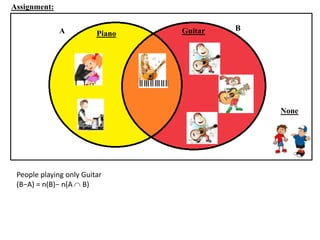
The document discusses methods for defining and representing sets, including examples of set listings (roster form) and rules (set builder form). It includes practical applications of sets in terms of height comparisons among students and Venn diagrams related to game participation. The document concludes with assignments and additional calculations regarding participants in different activities.

1. SETS
STD- IX
(Algebra)
By Natasha Pereira

2. The heights (in cm) of 8 girls in class X are as follows:
Girl A B C D E F G H
Height(in cm) 152 155 156 153 160 157 154 159
1)List the tall girls in the class
(Different students will give different answers)

3. The heights (in cm) of 8 girls in class X are as follows:
Girl A B C D E F G H
Height
(in cm)
152 155 156 153 160 157 154 159
2) Give me a group of girls whose height is greater than >156 cm.
i) {A, B, C }
ii) {C, E, F , H}
iii) {E, F, H}
Now you are able to give a correct answer because it a well defined
collection of objects.

4. What is a Set?
-A set is a collection of well defined objects
Examples:
1) A set of colors in a rainbow 2) A set of days in a week
3) A set of vowels in the English alphabet

5. Methods of Writing Sets
1) Listing method (Roster form)
2) Rule method (Set builder form)

6. 1) Listing method (Roster form)
Its simple - Listing means to list out
Examples:
i) A is a set of vowels
A = { a, e, i , o, u }
ii) B is a set of Prime numbers between 10 to 20
B = {11, 13, 17, 19}
iii) C is a set of first five cubes
C = {1, 8, 27, 64, 125}
iv) D is a set of letters of the word DIVISION
D = { D, I, V, S, O, N }

7. 2) Rule method (Set builder form)
As the word rule means- it follows a certain form of rule
Examples:
i) Consider the set A ={1, 4, 9, 16, 25}
Rule method: A = {x|x=n² , n N, n=1,2,3,4,5}
It is read as: x such that x=n² , n belongs to a Natural number
and n=1,2,3,4,5
ii) Consider the set B= {11, 13, 17, 19}
Rule Method: B={x|x is a Prime number, 10 < x < 20}
iii) Consider the set C={−3, −2, −1, 0, 1, 2, 3}
Rule method: C={x|x is an integer, −3 x 3 }

8. Illustration:
Listing method
(Roster form)
Rule method
(Set builder form)
A = { a, e, i, o, u } A = {x|x is a vowel in English alphabet}
B= { 11, 13, 17, 19} B = { x|x is a prime number, 10< x <20}
C= {−3,−2,−1, 0, 1 ,2,3} C={x|x is an integer, and −3 x 3 }
D= { 1, 4, 9, 16, 25 } D = {x|x =n² , and n= 1,2,3,4,5}

9. Look at the Venn diagram and answer:
Football Tennis
Both Games
No Games
Q) How many people are there in all?
Ans: 13 People
Q) How many people play Football?
Ans: 7 People
Q) How many people play only Football?
Ans: 5 People

10. Look at the Venn diagram and answer:
Football Tennis
Both Games
No Games
Q) How many people play Tennis?
Ans: 5 People
Q) How many people play only Tennis?
Ans: 3 People

11. Look at the Venn diagram and answer:
Football Tennis
Both Games
No Games
Q) How many people play both the Games?
Ans: 2 People
Q) How many people play neither of the Games?
Ans: 3 People

12. Look at the Venn diagram and answer:
Football Tennis
Both Games
No Games
(A B)
A
B
(B−A)(A−B)
(A B)
U

13. Look at the Venn diagram and answer:
Football Tennis
Both Games
No Games
(A B)
A
B
(B−A)(A−B)
(A B)
U
Q) How many people are there in all?
Ans: U=13 people
Q) How many people play Football?
Ans: n(A)=7

14. Look at the Venn diagram and answer:
Football Tennis
Both Games
No Games
(A B)
A
B
(B−A)(A−B)
(A B)
U
Q) How many people play both Games?
Ans: (A B) = 2

15. Look at the Venn diagram and answer:
Football Tennis
Both Games
No Games
(A B)
A
B
(B−A)(A−B)
(A B) U
Q) How many people play Football?
Ans: n(A)= 7
Q) How many people play only Football?
Ans: n(A−B) = n(A) − n(A B)
= 7 − 2
= 5

16. Look at the Venn diagram and answer:
Football Tennis
Both Games
No Games
(A B)
A
B
(B−A)(A−B)
(A B) U
Q) How many people play Tennis?
Ans: n(B)= 5
Q) How many people play only Tennis?
Ans: n(B−A) = n(B) − (A B)
= 5 − 2
= 3

17. Look at the Venn diagram and answer:
Football Tennis
Both Games
No Games
(A B)
A
B
(B−A)(A−B)
(A B) U
Q) How many people play atleast one of the two Games?
Ans: n(A B) = 10
Q) How many people play neither of the Games?
Ans: n(A B) = 3

18. Assignment:
Piano GuitarA B
None
n (U) = *Only Piano (A−B) =
(A B)= *Only Guitar(B−A) =
(A B)=
(A B) =
n(A)=
n(B) = *Use the formula (A−B) = n(A)− n(A B)

19. Assignment:
Piano GuitarA B
Both
None
n (U) =

20. Assignment:
Piano GuitarA B
None
n(A)=

21. Assignment:
Piano GuitarA B
None
n(B) =

22. Assignment:
Piano GuitarA B
None
(A B)=

23. Assignment:
Piano GuitarA B
None
(A B) =

24. Assignment:
Piano GuitarA B
None
(A B) =

25. Assignment:
Piano GuitarA B
None
*Only Piano (A−B) =
Use the formula (A−B) = n(A)− n(A B)

26. Assignment:
Piano GuitarA B
None
People playing only Guitar
(B−A) = n(B)− n(A B)

27. THE END
Thank you
Happy studying