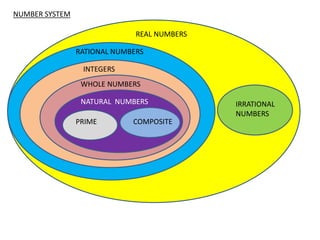
The document discusses various number theory concepts including: - Types of numbers like natural numbers, whole numbers, integers, rational numbers, irrational numbers, prime numbers, and composite numbers. - Euclid's division lemma and how it can be used to express integers in certain forms. - Fundamental theorem of arithmetic and prime factorisation of numbers. - Properties of rational numbers like their representation as fractions and different types of decimal expansions. - Proofs that some numbers like square roots of 2 and 5 are irrational using contradiction.

1. NUMBER SYSTEM
IRRATIONAL
NUMBERS
RATIONAL NUMBERS
INTEGERS
WHOLE NUMBERS
NATURAL NUMBERS
PRIME COMPOSITE
REAL NUMBERS

2. EUCLID’S DIVISION LEMMA:
Given positive integers a and b, there exist unique integers q
& r satisfying a= bq+ r, 0 r  b.
Eg: for a= 20, b= 6
We have 20= 6  q + r
20= 6  3 + 2 , 0  2< 6
20= 6  4
20 = 6  2 + 8 , 0  8  6

3. Show that any positive even integer can be written in the form 6q, 6q+2,
6q+4, where q is an integer
Let a be any positive integer, b=6 then by division algorithm we have
a= 6q + r, where 0 r  6 ( r= 0, 1, 2, 3, 4, 5)
 a= 6q a=6q+1 a=6q+2 a=6q+3 a=6q+4 a=6q+5
K= 3q
6q= 23q=2k
a= 2k a=2k+1 a=2k+2 a= 2k+3 a=2k+4 a= 2k+5
Odd Even EvenEven Odd Odd
So we can have any positive even integers is of the form
6q 6q+2 6q+4

4. Use Euclid’s division lemma to show that the cube of any integer is of the
form 9m, 9m+1, 9m+8
Let a be any positive integer, by division lemma we have
a= 3q + r , where 0r3 (r= 0, 1, 2)
a= 3q a= 3q+1 a=3q + 2

5. An army contingent of 616 members is to march behind an army band of
32 members in a parade. The two groups are to march in the same number
of columns. What is the maximum number of columns in which they can
march?
HCF (616, 32) = 8
Home Work: Exercise 1.1 -2,4

6. Fundamental theorem of Arithmetic
Every Composite number can be expressed (factorised ) as the product of
Primes, and this factorisation is unique , apart from the order in which the
prime factors occur.
4 = 2  2
6 = 3  2
9 =   
10 = 5  2
Example: Consider the number , where n is a natural number. Check
whether there is any value of n for which ends with the digit zero.
Any number end with a digit zero, will be divisible by 5

7. Example: Find the LCM and HCF of 6 and 20 by the prime
factorisation method.
HCF (6, 20)= Product of the smallest power of each common
prime factor in the numbers = 2
LCM(6, 20)= Product of the greatest power of each prime factor,
involved in the numbers = 22  5  3
For any two positive integers a and b,
HCF ( a, b )  LCM ( a, b ) = a  b
Home Work: Exercise 1.2- 1, 2, 3,

8. Example:
Find the HCF of 96 and 404 by the prime factorisation method.
Hence,find their LCM.
Solution : The prime factorisation of 96 and 404 gives :
96 = 25 × 3, 404 = 22 × 101
Therefore, the HCF of these two integers is 22 = 4.
Also, LCM(96, 404) HCF(96, 404)= 96404

9. Example:
Find the HCF and LCM of 6, 72 and 120, using the prime
factorisation method.
Solution : We have :
6 = 2 × 3, 72 = 23 × 32, 120 = 23 × 3 × 5
Here, 21 and 31 are the smallest powers of the common factors
2 and 3, respectively.
So, HCF (6, 72, 120) = 21 × 31 = 2 × 3 = 6
23, 32 and 51 are the greatest powers of the prime factors 2, 3
and 5 respectively involved in the three numbers.
So, LCM (6, 72, 120) = 23 × 32 × 51 = 360
Remark : Notice, 6 × 72 × 120  HCF (6, 72, 120) × LCM (6, 72,
120). So, the
product of three numbers is not equal to the product of their
HCF and LCM.

10. EXERCISE 1.2-6
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are
composite numbers.
7 × 11 × 13 + 13 = 13 × (7 × 11 + 1 )
= 13 × (77+1) = 13 × 78 = 13 × 2 × 3 × 13 and
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 = 5 × (7 × 6 × 4 × 3 × 2 +1)
= 5 × (1008 + 1) = 5 × 1009
Since both the numbers can be expressed as product of more than one
prime number, that are composite number.

11. EXERCISE 1.2-7
There is a circular path around a sports field. Sonia takes 18
minutes to drive one round of the field, while Ravi takes 12
minutes for the same. Suppose they both start at the same
point and at the same time, and go in the same direction. After
how many minutes will they meet again at the starting point?
Sonia= n1 times Ravi= n2 times
n1  18 = n2  12 =(T min)
LCM (12, 18) =
18 = 2  3  3 = 21  32
12 = 2  2  3 = 22  31
LCM (12, 18) = Greatest powers of the prime
factors
= 22  32 = 36, After 36 minutes Ravi and Sonia
will meet again.

12. EXERCISE 1.2
4. Given that HCF (306, 657) = 9, find LCM (306, 657).
Solu: LCM (306, 657)= (306  657)  HCF (306, 657)
LCM (306, 657) = 201042  9
= 22338
5. Check whether 6n can end with the digit 0 for any natural number n.
Solu : 6n = (2  3)n
= 2n  3n
Any number end with digit 0, will be divisible by 5. The primes in the
factorisation of 6n are 2 and 3. So, the uniqueness of the Fundamental
Theorem of Arithmetic guarantees that there are no other primes in the
factorisation of 6n. So, there is no natural number n for which 6n ends with
the digit zero.

13. Irrational Numbers
A number ‘s’ is called irrational if it cannot be written in the form , pq where p
and q are integers and q  0.
Eg: you are already familiar, are : 2,2/3, 3, 15 , 0.10110111011110,  ,
etc.
Theorem: Let p be a prime number. If p divides a2, then p divides a, where
a is a positive integer.

14. Theorem 1.4 :  2 is irrational.
Proof: Let us assume, to the contrary, that  2 is rational.
 2 = a/b ; where a and b are coprimes.
b 2 = a
Squaring on both sides, we get 2b2 = a2.
 2 Divides a2, then by previous theorem we have 2 divides a, since 2 is a
prime .
So, we can write a = 2  k, for some integer k.
Substituting for a, we get 2b2 = 4k2,
that is, b2 = 2k2.
2 Divides b2 , then by previous theorem we have 2 divides b, since 2 is a
prime .
Therefore, a and b have at least 2 as a common factor.
But this contradicts the fact that a and b have no common factors other
than 1.
So our assumption that  2 is rational, is incorrect .
So, we conclude that 2 is irrational.
Home Work:- EXERCISE 1.3 1, 3

15. EXERCISE 1.3
2. Prove that 3 + 2 5 is irrational.
Proof: Let us assume, to the contrary, that 3 + 2 5 is rational.
3 + 2 5 = a/b ; where a and b are coprimes.
25 = a/b – 3
5 = ½(a/b – 3)
5 = Rational
But we know that 5 is irrational. So we can conclude that 3 + 2 5
is irrational.

16. Rational Numbers and Their Decimal Expansions
Rational numbers are of the form p/q , where q  0 and its expansion has
either a terminating decimal expansion or non terminating repeating
decimal expansion.
Example: Terminating decimal - 0.375, 0.104, 3.3408.
Non Terminating repeating decimal– 1.010101....., 0.4714714714......

17. Theorem 1.5 : Let x be a rational number whose decimal expansion terminates.
Then x can be expressed in the form ,p/q where p and q are coprime, and the
prime factorisation of q is of the form 2n5m, where n, m are non-negative
integers.
X = Terminating rational
p and q are co primes
Theorem 1.6 : Let x =p/q be a rational number, such that the prime
factorisation of q is of the form 2n5m, where n, m are non-negative integers.
Then x has a decimal expansion which terminates.

18. Theorem 1.7 : Let x =p/q, where p and q are coprimes, be a rational number,
such that the prime factorisation of q is not of the form 2n5m, where n, m are
non-negative integers. Then, x has a decimal expansion which is non-
terminating repeating (recurring).
Home Work:- EXERCISE 1.4 – 1,2

19. EXERCISE 1.4- 3
The following real numbers have decimal expansions as given below. In each
case, decide whether they are rational or not. If they are rational, and of the
form , p/q what can you say about the prime factors of q?
(i) 43.123456789 (ii) 0.120120012000120000. . . (iii) 43.123456789
43.123456789123456789123456789...
Ans: (i) Here the decimal expansion is terminating decimal. Therefore it is a
rational number.
The prime factors of its denominator are of the form 2m  5n, n, m are non
negative integers .
(ii) Here the number is non terminating also non repeating.
(iii) Here the expansion is non terminating repeating. Therefore it is rational
and denominator is of the form 2m  5n, n, m are non negative integers .

20. Extra Problems
1. Find a rational number between 2 and 3.
Solu: let p be a rational number between 2 and 3 then, 2< p < 3
Squaring throughout; 2< p2 < 3
Perfect squares lie between 2 and 3 = 2.25, 2.56, 2.89
2< 2.25 < 2.56 < 2.89 < 3
Taking square root throughout;  2< 1.5 < 1.6 <1.7 <  3
So the rational numbers between  2 and  3 are : 1.5, 1.6, 1.7... Etc
2. The decimal expansion of the rational number 43/ 2453, will terminate after
how many places of decimal?
Solu: 4 > 3
 43/ 2453 will terminates after 4 places of decimal.
The decimal expansion of rational number of the type p/2m5n, where m, n
are non negative integers will terminate after m places of decimal if m is
bigger than n, or n places of decimal if n is bigger than m

21. 3. Show that cube root of 6 is irrational.
Assume cube root 6 is rational. Then let cube root 6 = a/b ( a & b are co-prime
and b  0)
Cubing both sides : 6=a3/b3
a3 = 6b3
a3 = 2(3b3)
Therefore, 2 divides a3 or a2  a . By Euclid's Lemma if a prime number
divides the product of two integers then it must divide one of the two integers
Since all the terms here are the same we conclude that 2 divides a.
Now there exists an integer k such that a=2k
Substituting 2k in the above equation
8k3 = 6b3
b3 = 2{(2k3) / 3)}
Therefore, 2 divides b3. Using the same logic as above. 2 divides b.
Hence 2 is common factor of both a & b. But this is a contradiction of the fact
that a & b are co-prime. Therefore, the initial assumption is wrong.
cube root 6 is irrational.

22. 4. Prove that, if x and y are odd positive integers, then x2+y2 is even
but not divisible by 4.
Solution: We know that any odd positive integer is of the form 2q+1,
where q is an integer.
So, let x=2m+1 and y=2n+1, for some integers m and n. we have x2+y2
x2+y2 =(2m+1)2+(2n+1)2
x2+y2 = 4m2+1+4m+4n2+1+4n=4m2+4n2+4m+4n+2
= 4(m2+n2)+4(m+n)+2=4{(m2+n2)+(m+n)}+2
= 4q+2, when q=(m2+n2)+(m+n)
x2+y2 is even and leaves remainder 2 when divided by 4.
x2+y2 is even but not divisible by 4.

23. 6. Determine the no. nearest to 110000 but greater than 100000 which is exactly
divisible by 8,15 and 21.
Solution: The number which is divisible by 8, 15, and 21 is also divisible by the L.C.M of
the number 8, 15 and 21. The L. C. M of 8, 15, and 21 is calculates as:
Thus, the number less than 110000 and nearest to 110000 that is divisible by 840 is
110000 – 800 = 109200
Now, 109200 is also greater than 100000.
Thus, the number nearest to 110000 and greater than 100000 which is exactly divisible
by 8, 15, and 21 is 109200.