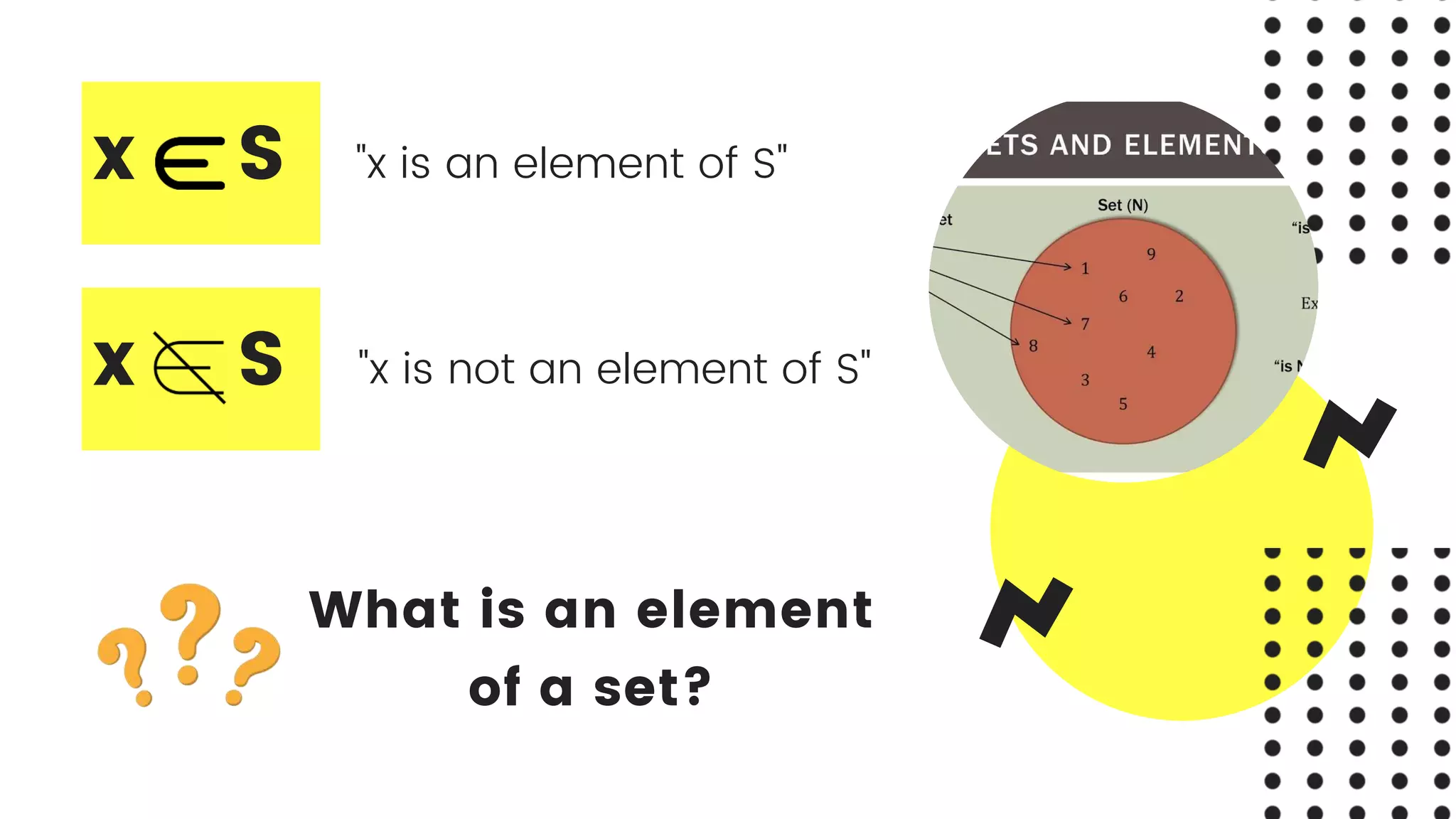
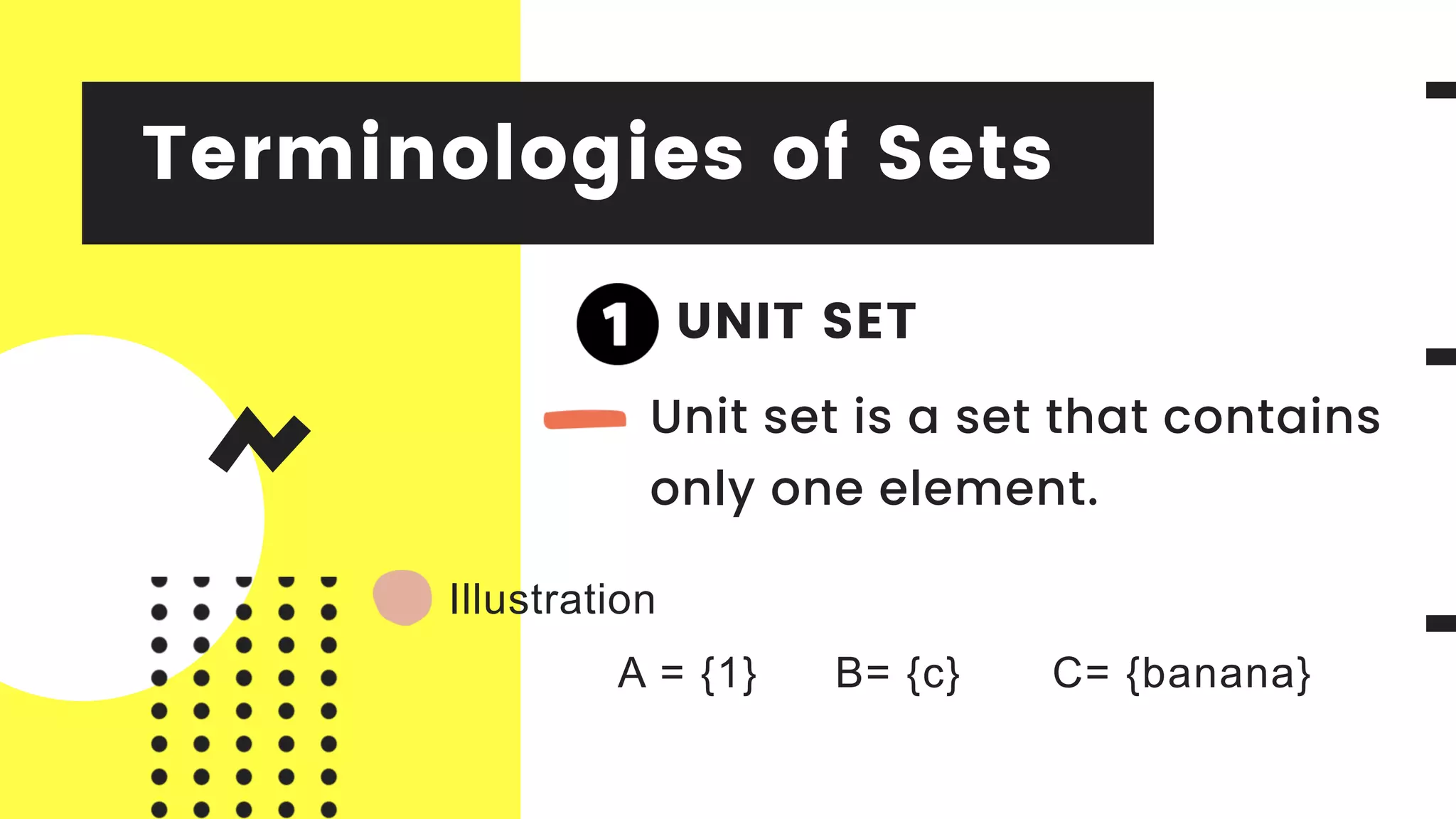
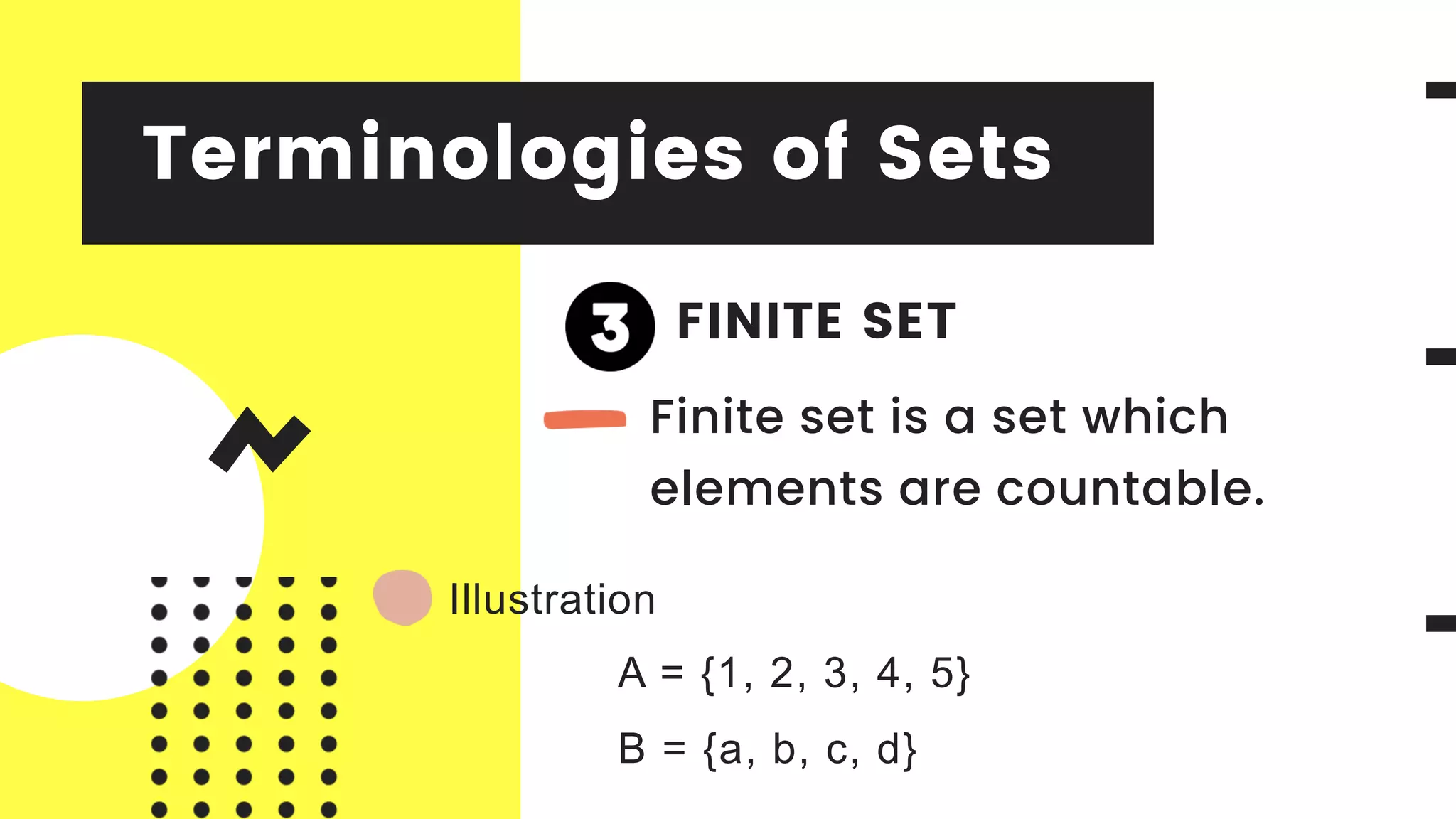
This document discusses four basic concepts in mathematics: sets and operations on sets, relations, functions, and binary operations. It provides definitions and examples of key terms related to sets, including elements of a set, subsets, union, intersection, difference, complement, and Cartesian product. Operations on sets such as union, intersection, and difference are defined using set notation. Examples are given to illustrate concepts like subsets, equal sets, disjoint sets, and the Cartesian product.

1. FOUR
BASIC
CONCEPTS
GE 103
JUAN MIGUEL I. TANGKEKO

2. Four Basic
Concepts
SETS AND ITS BASIC
OPERATIONS
RELATIONS
FUNCTIONS
BINARY OPERATIONS

3. Sets and its
basic
operations
Four Basic Concepts
LESSON 1

4. DEFINITION
In Math, sets are a collection of well-
defined objects or elements. A set is
represented by a capital letter symbol and
the number of elements in the finite set is
represented as the cardinal number of a
set in a curly bracket {…}.

5. EXAMPLES
1. A set of counting numbers from 1 to
10.
2. A set of English alphabet from a to c.
3. A set of integers.
1. A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
2. B = {a, b, c}
3. C = {.... -3, -2, -1, 0, 1, 2, 3, ...}

6. x S
x S
"x is an element of S"
"x is not an element of S"
What is an element
of a set?

7. The language of Sets
The notation means that
an item belongs to a set.
1 A 3 A 6 A
Pertains to each member of
the set.
Illustration
Say A = {1, 2, 3, 4, 5}
5 A
ELEMENT
OF A SET

8. Terminologies of Sets
Unit set is a set that contains
only one element.
UNIT SET
Illustration
A = {1} B= {c} C= {banana}

9. Terminologies of Sets
Empty or null set is a set that
has no element.
EMPTY SET or NULL SET;
Illustration
A = {}
A set of seven yellow
carabaos.

10. Terminologies of Sets
Finite set is a set which
elements are countable.
FINITE SET
Illustration
A = {1, 2, 3, 4, 5}
B = {a, b, c, d}

11. Terminologies of Sets
Infinite set is a set which
elements are not countable or
has no end.
INFINITE SET
Illustration
Set of counting numbers
A = {.... -3, -2, -1, 0, 1, 2, 3, ...}

12. Terminologies of Sets
Total number of the elements
in a set.
CARDINAL NUMBER; n
Illustration
A = {2, 4, 6, 8}
B = {a, c, e}
n = 4
n = 3

13. Two sets are said to be equal iff the
have equal number of cardinality and
the elements are identical.
EQUAL SET
Illustration
A = {1, 2, 3, 4, 5}
B = {3, 5, 2, 1, 4}
A and B are
equal sets
Terminologies of Sets

14. Two sets are said to be equivalent if the
Sets have the exact number of elements.
There is a 1-1 correspondence.
EQUIVALENT SET
Illustration
A = {1, 2, 3, 4, 5}
B = {a, b, c, d, e}
A and B are
equivalent
sets
Terminologies of Sets

15. Universal set is the set of all
elements under discussion
UNIVERSAL SET; U
Illustration
A set of an English alphabet
U = {a, b, c, d, ...z}
Terminologies of Sets

16. Two sets, say A and B, are said to
be joint iff they have common
element/s.
JOINT SETS
Illustration
A = {1, 2, 3}
B = {2, 4, 6}
A and B are joint sets since
they have a common element,
2.
Terminologies of Sets

17. Two sets, say A and B, are said to be
disjoint iff they are mutually exclusive
or they don't have common element/s.
DISJOINT SETS
Illustration
A = {1, 2, 3}
B = {4, 6, 8}
A and B are disjoint sets since
they don't have a common
element.
Terminologies of Sets

18. TWO WAYS OF DESCRIBING A SET
It is done by listing or tabulating the
elements of the set.
ROSTER or TABULAR
METHOD
Illustration
A = {2, 4, 6}
B = {a, b, d, e, h, i}
C = {blue, red, yellow}

19. It is done by stating or describing the
common characteristics of the elements of
the set. We use the notation A = {x l x ...}
RULE or SET-BUILDER
METHOD
Illustration
A = {x l x is a counting number from 1 to 5}
B = {x l x English alphabet}
TWO WAYS OF DESCRIBING A SET

20. EXAMPLES

21. A subset, A B, means
that every element of A is
also an element of B.
If x A then, x B
SUBSETS
In particular, every set is a
subset of itself. A A

22. SUBSETS A subset is called a proper subset,
A is a proper subset of B, if there is
at least one element of B that is
not in A.
A B
A = {1, 3, 5, 7}
Illustration
B = {1, 3, 5, 7, 9, 11}
every element of A is an element of B
there is at least 1 element in B that is
not an element of A

23. The empty or null set, {} or , is a
subset of every set.
How many subsets are there in the set
Illustration
A = {1, 2, 3}
The number of subsets of a given
set is given by , n is the number
of elements of the given set.
2
n
List down all the subsets of A.
SUBSETS

24. Solution:
{1}
2
n
List of subsets:
Number of elements = 3
= 2
3
= 8
A has 8 subsets.
With one element
{2} {3}
With two elements
{1, 2} {1, 3} {2, 3}
With three elements
{1, 2, 3}
With no
element
{} or
SUBSETS

25. ORDERED PAIR
"b"
Given elements a and b, the symbol (a, b) denotes the
ordered pair consisting of a and b together.
"a" first element second element
two ordered pairs (a, b) and (c, d) are equal iff
a = c and b = d

26. ORDERED PAIR
(a, b) = (c, d)
Symbolically,
means that a = c and b = d
Illustration
If (a, b) = (3, 2)
then a = 3 and b = 2
Find x and y if (4x + 3, y) = (3x + 5, -2)
4x + 3 = 3x + 5 y = -2
4x - 3x = 5 - 3
x = 2

27. OPERATION ON SETS
A B
UNION OF SETS
The union of sets A and B, denoted by
is defined as
A B = {x l x A or x B}
Illustration
If A = {1, 2, 3} and B = {4, 5}, then
A B = {1, 2, 3, 4, 5}
If A = {1, 2, 3} and B = {1, 2, 4, 5}, then
A B = {1, 2, 3, 4, 5}

28. A B
UNION OF SETS
Illustration
OPERATION ON SETS

29. The intersection of sets A and B,
denoted by
A B = {x l x A and x B}
A B = {1, 2} A B = {} or
A B
INTERSECTION OF SETS
is defined as
Illustration
If A = {1, 2, 3} and B = {4, 5}, then
If A = {1, 2, 3} and B = {1, 2, 4, 5}, then
OPERATION ON SETS

30. A B
INTERSECTION OF SETS
Illustration
OPERATION ON SETS

31. The difference of sets A and B,
denoted by
A - B = {x l x A and x B}
A - B = {3} A - B = {1, 2, 3}
A - B
DIFFERENCE OF SETS
is defined as
Illustration
If A = {1, 2, 3} and B = {4, 5}, then
If A = {1, 2, 3} and B = {1, 2, 4, 5}, then
OPERATION ON SETS

32. A - B
DIFFERENCE OF SETS
Illustration
OPERATION ON SETS

33. For set A, the difference U - A, where U is the
universal set is called the complement of A,
denoted by . Thus it is the set of
everything that is not in A.
A
COMPLEMENT OF SETS
Illustration
Let U = {a, e, i, o u} and A = {a, e}, then
c
or A'
Ac
= {i, o, u}
OPERATION ON SETS

34. COMPLEMENT OF SETS
Illustration
A
c
OPERATION ON SETS

35. Given sets A and B, the cartesian product of A
and B, denoted by and read as "A cross
B", is the set of all ordered pair (a, b), where a
is in A and b is in B.
A x B
CARTESIAN PRODUCT
= {(a,b) l a A and b B}
A x B
Note that A x B is not equal to B x A
OPERATION ON SETS

36. CARTESIAN PRODUCT, cont'd
A x B = {(1, a), (1, b), (2, a), (2, b)}
Illustration
If A = {1, 2, } and B = {a, b}, what is A x B?
what is B x A?
B x A = {(a, 1), (a, 2), (b, 1), (b, 2)}
OPERATION ON SETS

37. Thank
you!
GE 103
JASMINE T. BELEN