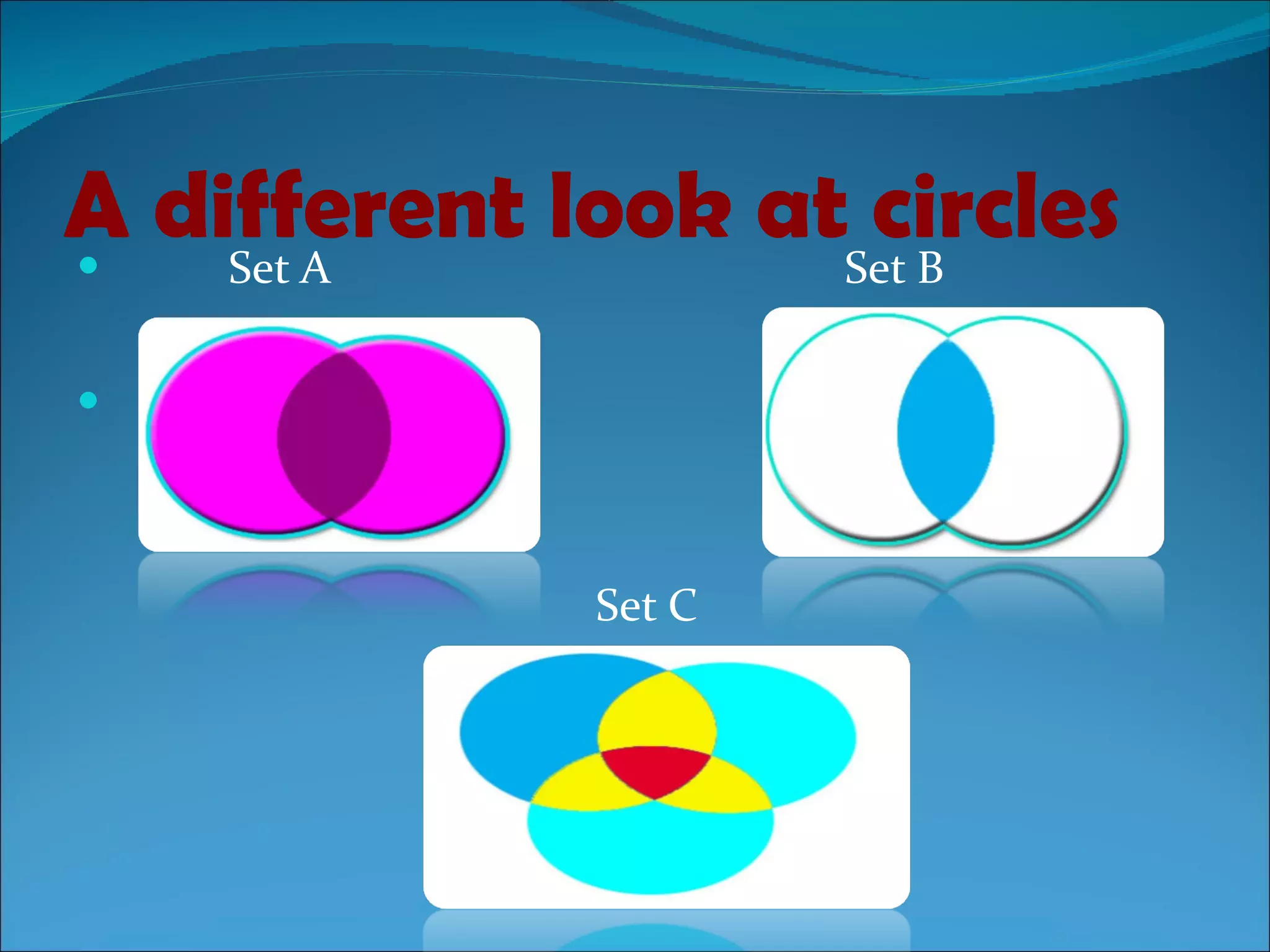
1) The document defines basic set terminology including sets, elements, subsets, finite and infinite sets, empty sets, equivalent sets, equal sets, and the universal set. 2) It provides an example of a situation where 80 students brought sandwiches, drinks, and canned goods to an outing, with various numbers of students bringing each item. 3) The key question is how many students did not bring any of the 3 kinds of items (sandwiches, drinks, canned goods).

1. (Sets and Subsets)

2. A different look at circles Set A Set B Set C

3. In an excursion at Pagsanjan Falls, 80 students brought sandwiches, drinks and canned goods as follows: 50 students brought sandwiches 30 students brought drinks 30 students brought canned goods 18 students brought canned goods and drinks 15 students brought sandwiches and canned goods 8 students brought sandwiches and drinks 5 students brought sandwiches, canned goods and drinks Question: How many students did NOT bring any of the 3 kinds?

4. SET - a well defined collection of distinct objects - CAPITAL LETTERS are used to represents set Example: A = {1, 2, 3, 4, 5} B = { M, A, T, H} C = { all even numbers}

5. ELEMENT - pertains to each object in a set - denoted by the symbol ______ which is read as "element of set ____” while the symbol____means “NOT an element of set _____” Example: A ={ 1, 2, 3, 4, 5} 3 ____ of set A 7 _____ of set A

6. BRACES { } - are used to enclose the elements of a given set Example: A = { x | x is an even integer} Set is read as “the set of all elements x, such that x is an even integer” B = { x | x is a letter in the word Math} “ the set of all elements of x, such that x is a letter in the word Math”

7. A = {x | x is a multiple of 3 between 3 and 18 } B = { x | x is a letter in the word Algebra} C ={ x | x is a positive odd number } A = { 3, 6, 9, 12, 15 } B = {A, L, G, E, B, R } C = {1,3, 5, 7, 9, 11, 13, ….} ROSTER/LISTING METHOD

8. Kinds of Sets: FINITE SET - a set whose number of elements can be counted Example: A = { -1, -2, -3, -4, -5 } B = { x | x is a multiple of 5 between 10 and 50} C = { x | x is a letter in the Philippine alphabet }

9. Kinds of Sets: INFINITE SET - a set whose number of elements CAN NOT be counted Example: A = { -1, -2, -3, -4, -5, . . . } B = { x | x is a multiple of 5 } C = { x | x is a name of a person}

10. Kinds of Sets: NULL / EMPTY SET - a set that has NO element - denoted by { } or O Example: A = { } B = O

11. EQUIVALENT SETS - two or more sets that have the same number of elements Example: A = {2, 4, 6, 8, 10 } B = { a, b, c, d, e} Sets A and B are equivalent sets.

12. EQUAL SETS - two or more sets that have the same elements Example: A = {2, 4, 6, 8, 10 } B = { 2, 4, 6, 8, 10 } Sets A and B are equal sets.

13. UNIVERSAL SET - the TOTALITY of ALL the elements in two or more given sets - denoted by “ U ” Example: A = { 2, 4, 6, 8 } B = { 1, 2, 3, 4 } U = { 1, 2, 3, 4, 6, 8} A = { a, b, c, d, e } B = { a, e, i, o, u } U = { a, b, c, d, e, i, o, u}

14. SUBSET - Set B is a subset of Set A if and only if ALL the elements in set B is in Set A Example: A = { 2, 4, 6, 8 } B = { 2, 4, 8 } Set B is a subset of Set A A = { a, b, c, d, e } B = { a, e, i, o, u } Set B is NOT a subset of Set A