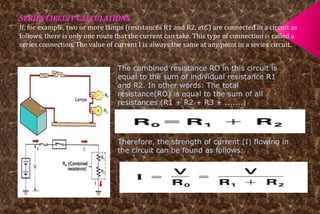
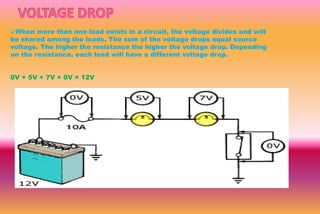
A series circuit consists of components connected in a single path, where the same current flows through each component, but the voltage is divided among them. If any part of the circuit is interrupted, the entire circuit fails, and the equivalent resistance can be calculated as the sum of individual resistances. Ohm's law relates the voltage drop across resistors to their resistance and the current flowing through them, indicating how energy is lost as charges move through the circuit.

2.  SERIES CIRCUITS
A series circuit is the simplest
circuit. The conductors, control and
protection devices, loads, and
power source are connected with
only one path to ground for current
flow. The resistance of each device
can be different. The same amount
of current will flow through each.
The voltage across each will be
different. If the path is broken, no
current flows and no part of the
circuit works. Christmas tree lights
are a good example; when one light
goes out the entire string stops
working.

3.  A Series Circuit has only one path to ground, so
electrons must go through each component to get
back to ground. All loads are placed in series.
 Therefore:
 1. An open in the circuit will disable the entire circuit.
 2. The voltage divides (shared) between the loads.
 3. The current flow is the same throughout the circuit.
 4. The resistance of each load can be different.

4.  Charge flows together through the external circuit at a rate
that is everywhere the same. The current is no greater at one
location as it is at another location. The actual amount of
current varies inversely with the amount of overall resistance.
There is a clear relationship between the resistance of the
individual resistors and the overall resistance of the
collection of resistors. As far as the battery that is pumping
the charge is concerned, the presence of two 6-Ω ;resistors in
series would be equivalent to having one 12-Ω resistor in the
circuit. The presence of three 6-Ω resistors in series would be
equivalent to having one 18-Ω resistor in the circuit. And the
presence of four 6-Ω resistors in series would be equivalent
to having one 24-Ω resistor in the circuit.

5. This is the concept of equivalent resistance.
The equivalent resistance of a circuit is the amount of
resistance that a single resistor would need in order to
equal the overall effect of the collection of resistors that
are present in the circuit. For series circuits, the
mathematical formula for computing the equivalent
resistance (Req) is
Req = R1 + R2 + R3 + ...
where R1, R2, and R3 are the
resistance values of the individual resistors that are
connected in series.

6. 20, 15, 10 5parallel
More Practice
Make, solve and check your own problems by using the Equivalent Resistance . The current
in a series circuit is everywhere the same. Charge does NOT pile up and begin to accumulate at
any given location such that the current at one location is more than at other locations. Charge
does NOT become used up by resistors such that there is less of it at one location compared to
another. The charges can be thought of as marching together through the wires of an electric
circuit, everywhere marching at the same rate. Current - the rate at which charge flows - is
everywhere the same. It is the same at the first resistor as it is at the last resistor as it is in the
battery. Mathematically, one might write

8. SERIES CIRCUIT CALCULATIONS
If, for example, two or more lamps (resistances R1 and R2, etc.) are connected in a circuit as
follows, there is only one route that the current can take. This type of connection is called a
series connection. The value of current I is always the same at any point in a series circuit.
The combined resistance RO in this circuit is
equal to the sum of individual resistance R1
and R2. In other words: The total
resistance(RO) is equal to the sum of all
resistances (R1 + R2 + R3 + .......)
Therefore, the strength of current (I) flowing in
the circuit can be found as follows:

10. When more than one load exists in a circuit, the voltage divides and will
be shared among the loads. The sum of the voltage drops equal source
voltage. The higher the resistance the higher the voltage drop. Depending
on the resistance, each load will have a different voltage drop.
0V + 5V + 7V + 0V = 12V

11. When current flows in a
circuit, the presence of a
resistance in that circuit will
cause the voltage to fall or drop
as it passes through the
resistance. The resultant
difference in the voltage on
each side of the resistance is
called a voltage drop. When
current (I) flows in the
following circuit, voltage drops
V1 and V2 across resistances R1
and R2 can be determined as
follows from Ohm's law. (The
value of current I is the same
for both R1 and R2 since they
are connected in series.)
The sum of the voltage drops across all
resistances is equal to the voltage of the power
source (VT):

14.  Conventional current is directed through the external circuit from the positive
terminal to the negative terminal. Since the schematic symbol for a voltage
source uses a long bar to represent the positive terminal, location A in the
diagram is at the positive terminal or the high potential terminal.
 An electric potential diagram is a conceptual tool for representing the
electric potential difference between several points on an electric circuit.
Consider the circuit diagram below and its corresponding electric potential
diagram.

15.  Ohm's law (ΔV = I • R) was introduced as an equation that relates the voltage
drop across a resistor to the resistance of the resistor and the current at the resistor.
The Ohm's law equation can be used for any individual resistor in a series circuit.
When combining Ohm's law with some of the principles already discussed on this
page, a big idea emerges.
The battery or source is represented by an escalator which raises charges to a higher level of
energy.
As the charges move through the resistors (represented by the paddle wheels) they do work
on the resistor and as a result, they lose electrical energy.
 The charges do more work (give up more electrical energy) as they pass through the larger
resistor.
By the time each charge makes it back to the battery, it has lost all the energy given to it by
the battery.