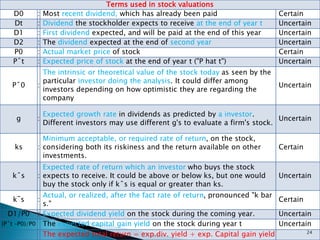
This document discusses various concepts related to bond valuation including: - Bonds provide periodic interest payments and repayment of face value at maturity as cash flows for valuation. - Key bond features that impact valuation are coupon rate, maturity date, par/face value, current yield. - Bond prices are sensitive to changes in market interest rates, with prices falling when rates rise. - Bond valuation involves discounting the coupon payments and face value repayment to their present value using the required rate of return. The document provides examples of calculating bond prices and yields using time value of money concepts. It also briefly discusses common stock valuation based on dividend payments and expected future sale price.

1. By
Sudarshan Kadariya
1

2. 2
The use of valuation models in
investment decisions (i.e., in decisions
on which assets are under valued and
which are over valued) are based upon
 a perception that markets are inefficient
and make mistakes in assessing value
an assumption about how and when
these inefficiencies will get corrected

3.  In an efficient market, the market price is
the best estimate of value. The purpose of
any valuation model is then the justification
of this value.
3

4.  In general, the value of an asset is the
equilibrium price that a buyer and a seller is
ready to transact.
 Note that if either the buyer or seller is not
both willing and able, then an offer does not
establish the value of the asset.
4

5.  Among the several types of value, the
following three are useful for valuation
purpose:
o Book Value - The asset’s accounting value after
depreciation
o Market Value - The price of an asset in the market
determined competitively
o Intrinsic Value - The present value of the expected
future cash flows discounted at the required rate of
return
5

6.  There are two primary determinants of the
intrinsic value of an asset as:
o The size and timing of the expected future cash
flows
o The individual’s required rate of return
(this is determined by a number of other factors such as risk/return
preferences, returns on competing investments, expected inflation,
etc.)
 Note that the intrinsic value of an asset can
be, and often is, different for each individual
so that the markets exist. (why??)
6

7. Bonds
 Bonds are long-term fixed income
securities. It is a trade-able instrument
which is also termed as debt securities. Both
the bonds (?) and debentures (?) are the debt
securities. Most commonly, bonds pay
interest periodically (usually semiannually)
and then return the principal at maturity.
 In India, debt securities issued by the
government and public sector are generally
referred as bonds whereas the debt
securities that are issued by the private
sector joint stock companies are called
debentures. The terms - bonds and
debentures are often used interchangeably.
7

8.  Par or Face Value
The amount of money that is paid to the bondholders at
maturity. For most bonds this amount is $1,000. It also
generally represents the amount of money borrowed by the
bond issuer.
 Coupon Rate
The coupon rate, which is generally fixed, determines the
periodic coupon or interest payments. It is expressed as a
percentage of the bond's face value. It also represents the
interest cost of the bond to the issuer. For example: if the
coupon rate is 12%, $120 is payable to bondholder.
8

9.  Spot interest rate
Zero coupon bond is a special type of bond which does
not pay annual interests. This type of bonds is also
called pure discount or deep discount bond. The
return received from a zero coupon bond expressed on
an annualized basis is the spot interest rate. In other
words, spot interest rate is the annual rate of return on
a bond that has only one cash inflow to the investor.
For instance, if a bond with face value $1000 issued at
a discount for $797.19 for 2 years. The spot rate is
12%, an annual interest rate.
 Coupon Payments
The coupon payments represent the periodic interest
payments from the bond issuer to the bondholder. For
example: coupon payments is $1000 @12% = $120. Since
most bonds pay interest semiannually, generally one half
of the annual coupon is paid to the bondholders every six
months.
9

10.  Maturity Date
The maturity date represents the date on which the bond
matures, i.e., the date on which the face value is repaid.
The last coupon payment is also paid on the maturity date.
 Current Yield
The current yield is the annual interest receivable on a
bond to its current market price. For instance, if the
market price is $800, coupon rate is 12% and the face
value is $1000 then the current yield equals $120/$800
* 100 = 15% (Discount or Premium ??)
(If the current yield > coupon rate = bond is selling at discount,
(If the current yield< coupon rate = bond is selling at premium)
10

11. THANK YOU
11

12.  Bonds are valued using time value of money
concepts.
 Their coupon, or interest, payments are treated
like an equal cash flow stream (annuity).
 Their face value is treated like a lump sum.
 How many types of cash flows that provides to a
bond investments or the bondholder?
 Periodic interest payments
 Repayment of the face value
12

13.  Maturity period: 10 years bond
 Date of purchase: January 1, 2003
 Face value: $1000
 Coupon rate: 10%
 Market rate of return: 12%.
 Required: Calculate the price of this bond today.
Draw a timeline
13
$100 $100
$100
$100
$100
$100
$100
$100
$100$100
$1000
+
?
?

14. 1. First of all calculate the present value of the coupon
stream
PV = $100/(1+.12)1 + $100/(1+.12)2 + $100/(1+.12)3 +
$100/(1+.12)4 + $100/(1+.12)5 + $100/(1+.12)6 +
$100/(1+.12)7 + $100/(1+.12)8 + $100/(1+.12)9+
$100/(1+.12)10
Or, we can find the PV of an annuity
PVA = $100 * {[1-(1+.12)-10]/.12} (PVIFA12%,10 years = 5.650)
PV = $565.02
2. Find the PV of the face value
PV = CFt / (1+r)t
PV = $1000/ (1+.12)10 (PVIF 12%, 10 years = 0.3219)
PV = $321.97
3. Add the two values to get the total PV
Therefore, the price of bond today is $565.02 + $321.97 =
$886.99
14

15.  If you purchased a bond for $800 5-years ago and sold
the bond today for $1200. The bond paid an annual 10%
coupon. What is the realized rate of return?
n
 PV = S [CFt / (1+r)t]
t=0
 $800 = [$100/(1+r) + $100/(1+r)2 + $100/(1+r)3 +
$100/(1+r)4 + $100/(1+r)5] + [$1200/(1+r)5]
 To solve, you need to use a “trail and error” approach.
 The realized rate of return on this bond is 19.3%.
 931.8276 (15%) & 781.3143 (20%)
15

16. 16
The following timeline illustrates a
typical bond’s cash flows:
0 1 2 3 4 5
100 100 100 100 100
1,000

17. The value of the bond is simply the
present value of the annuity-type
cash flow and the lump sum:
 
 
V Pmt
k
k
FV
k
B
d
N
d d
N

















1 1
1
1
17

18.  Assume that you are interested in purchasing a bond
with 5 years to maturity and a 10% coupon rate. If
your required return is 12%, what is the highest price
that you would be willing to pay?
0 1 2 3 4 5
100 100 100 100 100
1,000
 
 
VB 














100
1 1
1 012
012
1 000
1 012
927 90
5
5
.
.
,
.
.
18

19. 19
 Bond prices are sensitive to the market
interest rate
 If interest rates rise, the market value of
bonds fall in order to compete with newly
issued bonds with higher coupon rates.
 Sensitivity to the interest rate change become
more severe for longer term bonds
 Percentage change (rise) in price is not
symmetric with percentage decline.

20. 20
 The value of a bond depends on several
factors such as time to maturity, coupon rate,
and required return
 We can note several facts about the
relationship between bond prices and these
variables (ceteris paribus):
o Higher required returns lead to lower bond prices,
and vice-versa
o Higher coupon rates lead to higher bond prices,
and vice versa
o Longer terms to maturity lead to lower bond
prices, and vice-versa

21. THANK YOU
21

22. Common stock represents an ownership interest in a
corporation, but to the typical investor, a share of
common stock is simply a piece of paper characterized
by two features
◦ It entitles its owner to dividends, but only if the company has
earnings out of which dividend can be paid, and only if the
management chooses to pay dividends rather than retaining
and reinvesting all the earnings.
◦ Stock can be sold at some future data, hopefully at a price
greater than the purchase price. If the stock is actually sold at
a price above its purchase price, the investor will receive a
capital gain.
Stock price
 Volatile, rapidly changes
 Price swings are even larger for smaller companies
 For large companies, it is relatively stable
22

23.  Just like with bonds, the first step in valuing
common stocks is to determine the cash flows
 For a stock, there are two:
 Dividend payments
 The future selling price
 Again, find the present values of these cash
flows and adding them together will give us
the value
23

24. 24
Terms used in stock valuations
D0 : Most recent dividend, which has already been paid Certain
Dt : Dividend the stockholder expects to receive at the end of year t Uncertain
D1 : First dividend expected, and will be paid at the end of this year Uncertain
D2 : The dividend expected at the end of second year Uncertain
P0 : Actual market price of stock Certain
Pˆt : Expected price of stock at the end of year t ("P hat t") Uncertain
Pˆ0 :
The intrinsic or theoretical value of the stock today as seen by the
particular investor doing the analysis. It could differ among
investors depending on how optimistic they are regarding the
company
Uncertain
g :
Expected growth rate in dividends as predicted by a investor.
Different investors may use different g's to evaluate a firm's stock.
Uncertain
ks :
Minimum acceptable, or required rate of return, on the stock,
considering both its riskiness and the return available on other
investments.
Certain
kˆs :
Expected rate of return which an investor who buys the stock
expects to receive. It could be above or below ks, but one would
buy the stock only if kˆs is equal or greater than ks.
Uncertain
k¯s :
Actual, or realized, after the fact rate of return, pronounced "k bar
s."
Certain
D1/P0 : Expected dividend yield on the stock during the coming year. Uncertain
(Pˆt –P0)/P0 The expected capital gain yield on the stock during year t Uncertain
The expected total return = exp.div. yield + exp. Capital gain yield

25.  Assume that you are considering the purchase
of a stock which will pay dividends of $2 next
year, and $2.16 the following year. After
receiving the second dividend, you plan on
selling the stock for $33.33. What is the
intrinsic value of this stock if your required
return is 15%?
   
VCS 





2 00
1 15
216 3333
1 15
28571 2
.
.
. .
.
.
2.00 2.16
33.33
?
25





2
1
)1(
^
)1(t t
t
t
t
CS
ks
P
ks
D
V

26.  In valuing the common stock, we have
made two assumptions:
o We know the dividends that will be paid in the
future (Di)
o We know the price that we will be able to sell
the stock in the future (Pi)
 Both of these assumptions are unrealistic,
especially knowledge of the future selling
price
 Furthermore, suppose that when we intend
to hold the stock for twenty years, the
calculations would be very tedious!
26

27.  We cannot value common stock without making
some simplifying assumptions
 If we make the following assumptions, we can
derive a simple model for common stock
valuation:
Assumption 1: The holding period is infinite (i.e., you will
never sell the stock)
Assumption 2: The dividends will grow at a constant rate
forever
 Note that the second assumption allows us to
predict every future dividend, as long as we know
the most recent dividend
27

28.  With these assumptions, we can derive a
model which is known as the Dividend
Discount Model, or the Gordon Model
 This model gives us the present value of an
infinite stream of dividends that are growing
at a constant rate:
 V
D g
k g
D
k g
CS
CS CS





0 1
1
28
Where,
Ke = Kcs = Cost of equity
g = growth rate
Do = Recent dividend rate
D1 = One period dividend

29.  Recall the previous example in which the
dividends were growing at 8% per year, and
your required return was 15%
 The value of the stock must be:
 VCS 





185 1 08
15 08
2 00
015 08
2857
. .
. .
.
. .
.
(Note that this is exactly the same value that we got earlier)
29

30.  In the earlier example, how did we know that
the stock would be selling for $33.33 in two
years?
 Note that the period 3 dividend must be 8%
larger than the period 2 dividend, so:
 V2
216 1 08
15 08
2 33
015 08
3333





. .
. .
.
. .
.
30
(Therefore, the selling price is equal to 33.33, considering 8% growth rate per year)

31.  Preferred stock, like as bonds imposes a fixed
charge & the failure to make this fixed charge
will not lead to bankruptcy.
 Preferred stock represents an ownership claim on
the firm that is superior to common stock in the
event of liquidation.
 Typically, preferred stock pays a fixed dividend
periodically, and
 the preferred stockholders are usually not
entitled to vote as are the common shareholders.
31

32.  Most preferred stocks are perpetuities, and
the value of a share of perpetual preferred
stock is found as the dividend divided by the
required rate of return.
 Preferred stock is very much like common
stock, except that the dividends are constant
(i.e., the growth rate is 0%)
 Therefore, we can use the DDM with a 0%
growth rate to find the value:
 V
D
k
D
k
P
CS CS



0 1 0
0
32

33.  Suppose that you are interested in
purchasing shares of a preferred stock which
pays a $5 dividend every year. If your
required return is 7%, what is the intrinsic
value of this stock?
VP  
5
0 07
7143
.
.
33

34.  Two reasons:
First, the returns from investing from bonds
are less imperative and fixed.
Second, the bond prices fluctuate less than
the equity prices
34

35.  Yield to
Maturity:
 Same as
market
rate of
return at
maturity
 Yield to Call:
 Market rate of
return at call
which is
issuer’s option
 When
coupon>marke
t interest
35
 Current
Yield:
 Annual
interest
payment
divided
by
bond’s
current
price

36. 36
The yield to maturity (YTM) is the average annual
rate of return that a bondholder will earn. YTM is
generally the same as the market rate of interest,
kd which can be solve as “trial and error” or by
interpolation.
For example, a 14-year, 10 percent coupon with
par value $1000 is offered at a market price
$1494.93. What rate of interest we earn if we
bought the bond and held it to maturity?
(Answer is 5%)

37. F = Face Value = Par Value = $1,000
P = Bond Price
C = the semi annual coupon interest
N = number of semi-annual periods left to maturity
1YTM)annual-semi(1YTM
YTMannual-semi2YTM
2
n
P-F
MaturitytoYieldannual-Semi
2





PF
C
37

38.  Find the yield-to-maturity of a 5 year 6%
coupon bond that is currently priced at $850.
(assume the coupon interest is paid semi-annually.)
 Therefore there is coupon interest of $30 paid semi-
annually i.e. ($1000 x 6% = $60 p.a. & $30 s.a.)
 There are 10 semi-annual periods left until maturity
(i.e. nx2 = 5x2 = 10 periods)
38

39. %97.91)0486.1(1YTM)annual-semi(1YTMreturnofrateRealized
9.3%0.0927320.0486YTMannual-semi2YTM
0486.0
925$
30$15$
2
850,1$
30$
10
850$000,1$
2
n
P-F
MaturitytoYieldannual-Semi
22











PF
C
The approximation approach only gives us an approximate answer
39

40. THANK YOU
40