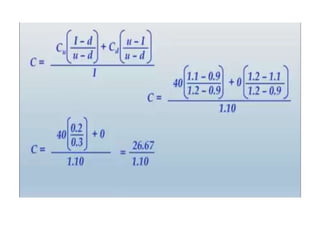
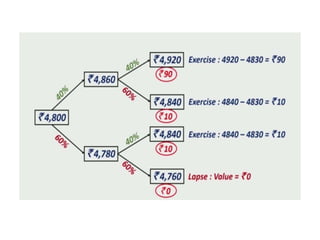
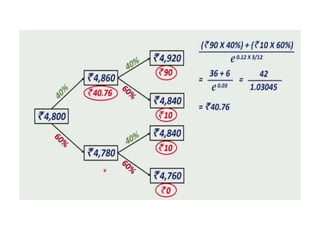
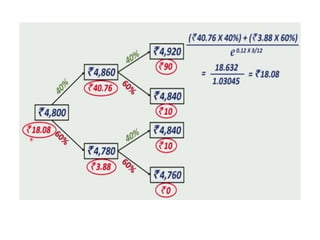
The document introduces the binomial option pricing model, which values options by allowing the underlying asset price to move up or down by a set percentage at each time period. It assumes two possible prices, constant interest rates over the life of the option, and perfect markets. The model is then demonstrated by calculating the possible up and down prices of a stock and related call option values at the next time period, given inputs like the current stock price, interest rates, and strike price.

1. Binomial Option Pricing
• By – Mr. Debasis Mohanty

2. • We begin with a single period.
• Then, we stitch single periods together to form the Multi-Period Binomial
Option Pricing Model.
• The Multi-Period Binomial Option Pricing Model is extremely flexible,
hence valuable; it can value American options (which can be exercised
early), and most, if not all, exotic options.
The Binomial Option Pricing Model
(BOPM)

3. Assumptions of the BOPM
• There are two (and only two) possible prices for the underlying asset on
the next date. The underlying price will either:
– Increase by a factor of u% (an uptick)
– Decrease by a factor of d% (a downtick)
• The uncertainty is that we do not know which of the two prices will be
realized.
• No dividends.
• The one-period interest rate, r, is constant over the life of the option (r%
per period).
• Markets are perfect (no commissions, bid-ask spreads, taxes, price
pressure, etc.)

4. The Stock Pricing ‘Process’
ST,d = (1+d)ST-1
ST,u = (1+u)ST-1
ST-1
Suppose that ST-1 = 40, u = 25% and d = -10%. What are ST,u and ST,d?
40
ST,u = ______
ST,d = ______
Time T is the expiration day of a call option. Time T-1 is one period
prior to expiration.

5. The Option Pricing Process
CT,d = max(0, ST,d-K) = max(0,(1+d)ST-1-K)
CT,u = max(0, ST,u-K) = max(0,(1+u)ST-1-K)
CT-1
Suppose that K = 45. What are CT,u and CT,d?
CT-1
CT,u = ______
CT,d = ______