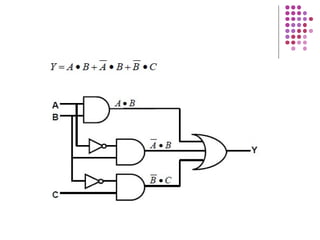
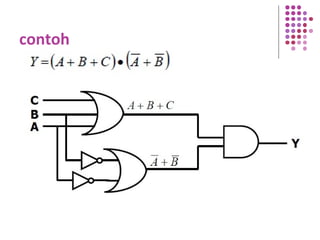
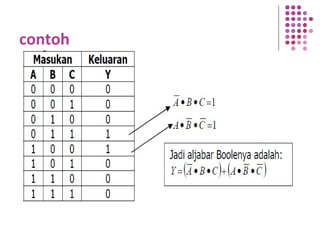
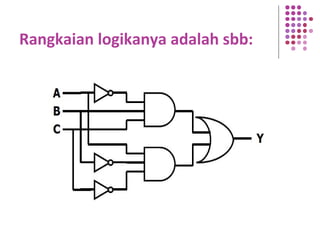
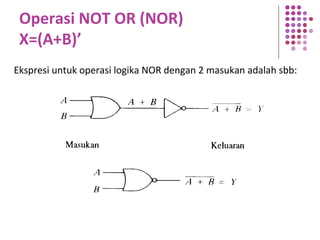
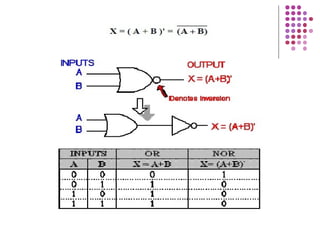
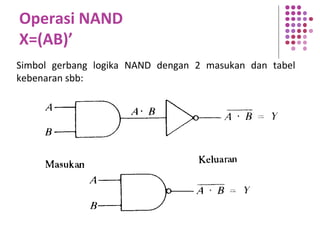
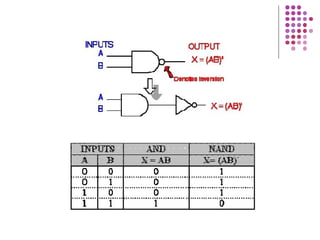
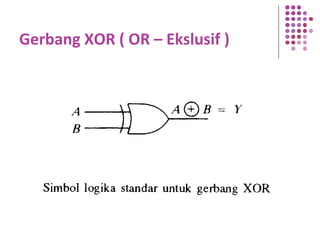
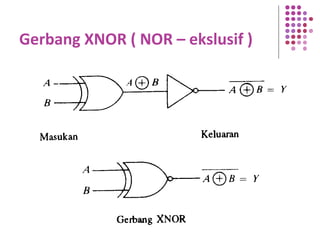
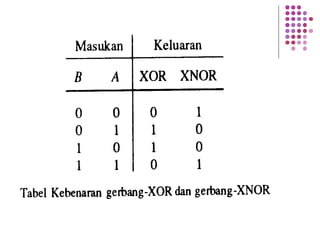
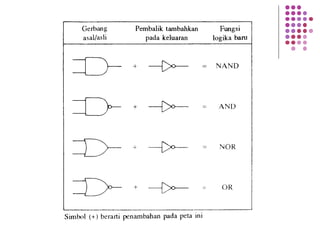
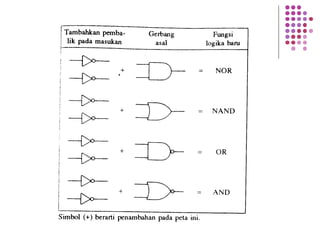
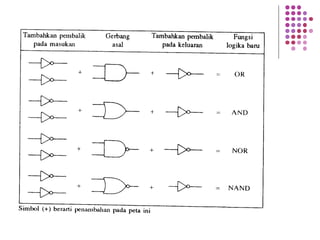
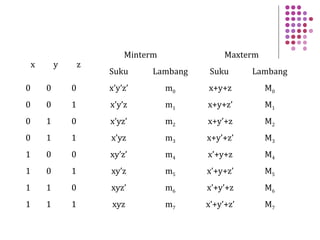
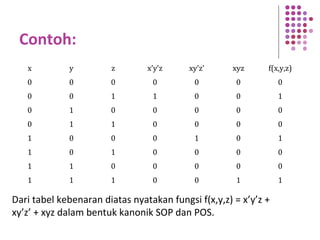
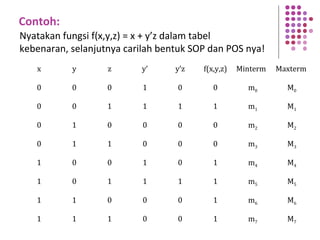
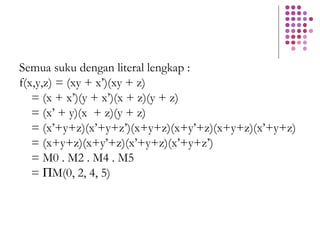Fungsi Boolean merupakan ekspresi yang dibentuk dari variabel Boolean melalui operasi penjumlahan, perkalian, atau komplemen. Dokumen menjelaskan berbagai konsep terkait fungsi Boolean seperti bentuk kanonik, fungsi komplemen, hukum De Morgan, dan konversi antara bentuk sum of product dan product of sum.

1. SISTEM DIGITALSISTEM DIGITAL
Kamis, 20 November 2014Kamis, 20 November 2014
Pertemuan VIIIPertemuan VIII
Trienani Hariyanti,Trienani Hariyanti,

2. PENGGUNAAN GERBANG LOGIKA
1. Penyusunan Rangkaian dari Aljabar
Boolean
Aljabar Boole merupakan dasar dalam
menyusun rangkaian logika. Sebagai contoh
kita mempunyai ekspresi/aljabar Boole sbb:
Y = A + B + C
rangkaian logikanya adalah sbb:

4. Latihan

5. 2. Aljabar/Ekspresi Boolean Maksterm
(Perkalian dari Penjumlahan / AND-OR)
Ekspresi Boolean Maksterm merupakan
perpaduan antara OR dan AND, yaitu
merupakan operasi AND dari OR
Artinya: “kita harus melakukan operasi-
operasi OR terlebih dahulu kemudian dari
hasil operasi OR tersebut kita AND-kan”

6. contoh

7. 3. Ekspresi Boolean Minterm (Penjumlahan
dari Perkalian / OR-AND)
Ekspresi Boolean minterm merupakan
kebalikan dari operasi Maksterm, yaitu
merupakan ekspresi OR-AND
Artinya:” Kita harus melakukan operasi-
operasi AND terlebih dahulu kemudian hasil
operasi AND kita OR-kan”.

8. Latihan

9. 4. Tabel Kebenaran dan Aljabar Boolean
Untuk menggambarkan rangkaian logika
selain menggunakan dasar aljabar Boole, kita
juga dapat menggunakan dasar dari tabel
kebenaran. Untuk dapat menggunakan tabel
kebenaran sebagai dasar penggambaran
rangkaian logika, terlebih dahulu dari tabel
kebenaran diubah dahulu ke dalam bentuk
aljabar Boole.

10. contoh

11. Rangkaian logikanya adalah sbb:

12. Latihan
Buatlah tabel kebenaran dan rangkaian logika
untuk aljabar Boole berikut ini:

13. Operasi NOT OR (NOR)
X=(A+B)’
Ekspresi untuk operasi logika NOR dengan 2 masukan adalah sbb:

15. Operasi NAND
X=(AB)’
Simbol gerbang logika NAND dengan 2 masukan dan tabel
kebenaran sbb:

17. Gerbang XOR ( OR – Ekslusif )

18. Gerbang XNOR ( NOR – ekslusif )

23. Fungsi Boolean
Fungsi Boolean adalah ekspresi yang
dibentuk dari peubah Boolean melalui
operasi penjumlahan, perkalian, atau
komplemen.
Contoh-contoh fungsi boolean :
1.f(x) = x
2.f(x,y) = x’y + y
3.f(x,y,z) = xyz’

24. Selain dengan cara aljabar, fungsi Boolean dapat
dinyatakan dalam bentuk tabel kebenaran.
Tabel kebenaran adalah suatu tabel yang
menyatakan seluruh kemungkinan nilai peubah
dari fungsinya.
Jika suatu fungsi Boolean memuat n peubah,
maka banyaknya baris dalam tabel kebenaran
ada 2n
.
Di dalam fungsi Boolean setiap peubah boolean
termasuk komplemennya disebut literal.

25. Contoh :
Buatlah tabel kebenaran dari fungsi aljabar Boolean
f(x,y,z) = xyz’ + x.
x y z z’ xyz’ f(xyz’ + x)
0 0 0 1 0 0
0 0 1 0 0 0
0 1 0 1 0 0
0 1 1 0 0 0
1 0 0 1 0 1
1 0 1 0 0 1
1 1 0 1 1 1
1 1 1 0 0 1

26. Fungsi Boolean tidak unik (tunggal), artinya
dua fungsi yang ekspresinya berbeda
dikatakan sama jika keduanya mempunyai
nilai yang sama pada tabel kebenaran untuk
setiap kombinasi peubah peubahnya.
Contoh:
f(x,y,z) = x’y’z + x’yz + xy’
dengan
g(x,y,z) = x’z + xy’

27. Prinsip Dualitas
• Dual dari suatu ekspresi dinyatakan
sebagai perubahan operator (. dan +) dan
(1 dan 0) di dalam ekspresi tersebut.
• Tidak dapat mengganti x dengan x’
• Dual tidak selalu sama dengan ekspresi asli.
Contoh:
Tentukan h(x,y,z) yang merupakan dual
dari f(x,y,z) = x’yz’ + x’y’z
h(x,y,z) = (x’+y+z’).(x’+y’+z)

28. Teorema 2.1
Untuk setiap elemen a, berlaku : a + a = a dan
a . a = a
Bukti
x + x = ( x + x ) (1) identitas
= ( x + x ) ( x + x’ ) komplemen
= x + ( x . x’ ) distributif
= x + 0 T8b
= x identitas
x.x = x.x + 0 identitas
= x.x + x.x’ komplemen
= x. ( x + x’ ) distributif
= x.1 T8a
= x identitas

29. Teorema 2.2
Untuk setiap elemen a, berlaku : a + 1 = 1 dan
a.0 = 0
Bukti
a + 1 = a + (a + a’) komplemen
= (a + a) + a’ asosiatif
= a + a’ T8a
= 1
a . 0 = a.(a.a’) komplemen
= (a.a) .a’ asosiatif
= a . a’ T8b
= 0

30. Teorema 2.3 (Hukum Penyerapan)
Untuk setiap elemen a dan b, berlaku :
a + a . b = a dan a . (a+b) = a
Bukti
a+ab = a.1 + a.b Identitas
= a . (1 + b) distributif
= a . 1 T7b
= a
a. (a+b)= a.a + a.b distributif
= a + ab idempoten
= a.1 + ab identitas
= a. ( 1 + b ) distributif
= a . 1 T7b
= a

31. Fungsi Komplemen
• Bila sebuah fungsi Boolean
dikomplemenkan, kita memperoleh
fungsi komplemen.
• Fungsi komplemen berguna pada saat
penyederhanaan fungsi boolean.
• Fungsi komplemen dari f, yaitu f’ dapat
dicari dengan menukarkan nilai 0
menjadi 1 dan nilai 1 menjadi 0

32. Ada dua cara yang dapat digunakan
untuk membentuk fungsi komplemen:
1. Menggunakan hukum De Morgan
Hukum De Morgan untuk dua buah peubah
(berlaku untuk n peubah), x1 dan x2, adalah:
1.(x1 + x2)’ = x1’x2’
• (x1x2)’ = x1’+ x2’
• (x1 + x2 + K + xn)’ = x1‘x2‘K xn‘
Dan dualnya:
(x1x2K xn)’ = x1’+ x2’+ K + xn’

33. Contoh:
f(x,y,z) = x(y’z’+yz) maka
f’(x,y,z) = (x(y’z’ + yz))’
= x’ + (y’z’+yz)’
= x’ + (y’z’)’ (yz)’
= x’ + (y + z) (y’ + z’)

34. 2. Menggunakan Prinsip Dualitas
Cari dual dari f, lalu komplemenkan setiap
literalnya.
contoh:
f(x,y,z) = x(y’z’+yz) maka
dual dari f: x + ( y’ + z’) (y + z)
komplemenkan tiap literalnya: x’ + (y + z) (y’ + z’) = f’
jadi, f’(x,y,z) = x’ + (y + z) (y’ + z’)

35. Latihan Soal
1.Tentukan dualitas dari fungsi Boolean
berikut:
a)f(x,y) = (x+y)’
b)f(x,y,z) = xy + x’z +yz
c)f(x,y) = xy + x’z + x’y’
2.Tentukan komplemen dari fungsi Boolean
berikut:
a)f(x,y,z) = x’yz’ + x’y’z
b)f(x,y,z) = x(y’z’ + yz)

36. Bentuk Kanonik
Bentuk kanonik adalah fungsi Boolean yang
dinyatakan sebagai jumlah dari hasil kali, hasil kali
dari jumlah dengan setiap suku mengandung literal
yang lengkap.
Ada dua macam bentuk kanonik:
•Minterm atau sum of product (SOP): Jumlah dari
perkalian
•Maxterm atau product of sum (POS): perkalian
dari jumlah

37. x y
Minterm Maxterm
Suku Lambang Suku Lambang
0 0 x’y’ m0 x+y M0
0 1 x’y m1 x+y’ M1
1 0 xy’ m2 x’+y M2
1 1 xy m3 x’+y’ M3
Tabel kebenaran untuk Minterm dan Maxterm

38. x y z
Minterm Maxterm
Suku Lambang Suku Lambang
0 0 0 x’y’z’ m0 x+y+z M0
0 0 1 x’y’z m1 x+y+z’ M1
0 1 0 x’yz’ m2 x+y’+z M2
0 1 1 x’yz m3 x+y’+z’ M3
1 0 0 xy’z’ m4 x’+y+z M4
1 0 1 xy’z m5 x’+y+z’ M5
1 1 0 xyz’ m6 x’+y’+z M6
1 1 1 xyz m7 x’+y’+z’ M7

39. Contoh:
x y z x’y’z xy’z’ xyz f(x,y,z)
0 0 0 0 0 0 0
0 0 1 1 0 0 1
0 1 0 0 0 0 0
0 1 1 0 0 0 0
1 0 0 0 1 0 1
1 0 1 0 0 0 0
1 1 0 0 0 0 0
1 1 1 0 0 1 1
Dari tabel kebenaran diatas nyatakan fungsi f(x,y,z) = x’y’z +
xy’z’ + xyz dalam bentuk kanonik SOP dan POS.

40. Penyelesaian
SOP
Perhatikan kombinasi peubah yang
menghasilkan nilai 1
Bentuk kanonik SOP dari fungsi f(f,y,z) = x’y’z +
xy’z’ + xyz
Dalam bentuk lain adalah:
f(x,y,z) = x’y’z + xy’z’ + xyz
= m1 + m4 + m7
= ∑ (1,4,7)

41. POS
Perhatikan kombinasi peubah yang
menghasilkan nilai 0
Bentuk kanonik SOP dari fungsi f(x,y,z) = x’y’z
+ xy’z’ + xyz
Dalam bentuk lain adalah:
f(x,y,z) = (x+y+z)(x+y’+z)(x+y’+z’)(x’+y+z’)(x’+y’+z)
= M0M2M3M5M6 = Π(0,2,3,5,6)

42. Contoh:
Nyatakan fungsi f(x,y,z) = x + y’z dalam tabel
kebenaran, selanjutnya carilah bentuk SOP dan POS nya!
x y z y’ y’z f(x,y,z) Minterm Maxterm
0 0 0 1 0 0 m0 M0
0 0 1 1 1 1 m1 M1
0 1 0 0 0 0 m2 M2
0 1 1 0 0 0 m3 M3
1 0 0 1 0 1 m4 M4
1 0 1 1 1 1 m5 M5
1 1 0 0 0 1 m6 M6
1 1 1 0 0 1 m7 M7

43. SOP
Perhatikan kombinasi peubah yang
menghasilkan nilai 1
Bentuk kanonik SOP dari fungsi
f(f,y,z) = x’y’z + xy’z’ + xy’z + xyz’ + xyz
Dalam bentuk lain adalah:
f(x,y,z) = m1 + m4 + m5 + m6 + m7
= ∑ (1,4,5,6,7)

44. POS
Perhatikan kombinasi peubah yang
menghasilkan nilai 0
f(x,y,z) = (x+y+z)(x+y’+z)(x+y’+z’)
Dalam bentuk lain:
f(x,y,z) = M0M2M3 = Π(0,2,3)

45. konversi kebentuk SOP
Teorema:
x+x’ = 1 x.x’ = 0 x+x = x x.x =
x
Contoh:
Nyatakan fungsi f(x,y,z) = x + y’z dalam bentuk kanonik
SOP
f(x,y,z) = x + y’z (lengkapi literal pada tiap suku)
= x (y+y’) (z+z’) + y’z (x+x’)
= (xy+xy’)(z+z’) + xy’z + x’y’z
= xyz + xyz’ + xy’z + xy’z’ + xy’z + x’y’z
= xyz + xyz’ + xy’z + xy’z’ + x’y’z
= m7 + m6 + m5 + m4 + m1
= ∑(1, 4, 5, 6, 7)

46. Konversi ke bentuk POS
Nyatakan fungsi f(x,y,z) = xy + x’z dalam
bentuk kanonik SOP
Bentuk fungsi ke POS
f(x,y,z) = xy + x’z
= (xy + x’)(xy + z) distributif
= (x + x’)(y + x’)(x + z)(y + z) distributif
= (x’ + y)(x + z)(y + z) komplemen, identitas

47. Lengkapi literal untuk setiap suku agar sama
Suku-1  x’ + y = x’ + y + zz’
= (x’ + y + z)(x’ + y + z’)
Suku-2  x + z = x + z + yy’
= (x + y + z)(x + y’ + z)
Suku-3  y + z = xx’ + y + z
= (x + y + z)(x’ + y + z)

48. Semua suku dengan literal lengkap :
f(x,y,z) = (xy + x’)(xy + z)
= (x + x’)(y + x’)(x + z)(y + z)
= (x’ + y)(x + z)(y + z)
= (x’+y+z)(x’+y+z’)(x+y+z)(x+y’+z)(x+y+z)(x’+y+z)
= (x+y+z)(x+y’+z)(x’+y+z)(x’+y+z’)
= M0 . M2 . M4 . M5
= ΠM(0, 2, 4, 5)

49. Latihan Soal
1. Nyatakan fungsi f(x,y,z) = y’ + xy + x’yz
dalam tabel kebenaran.
2. Nyatakan fungsi Boolean f(x,y,z) = wxy +
yz + xy dalam bentuk POS.
3. Nyatakan fungsi f(x,y,z) =y’ + xy + x’yz’
dalam tabel kebenaran.

50. x y z f(x,y,z)
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 0
4. Carilah bentuk kanonik SOP dan POS dari
f(x,y,z) = y’ + xy + x’yz’
5. Carilah bentuk kanonik dari SOP dari fungsi
f(x,y,z) yang ditunjukkan pada tabel kebenaran
berikut ini.

51. 6. Nyatakan Fungsi Boolean f(x,y,z) = x’y’z + xz
+ yz dalam SOP
7. Nyatakan Fungsi Boolean f(w,x,y,z) = wxy + yz
+ xy dalam SOP
8. Nyatakan Fungsi Boolean f(x,y,z)= (x+z)(y’+z’)
dalam POS