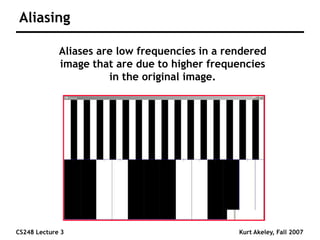
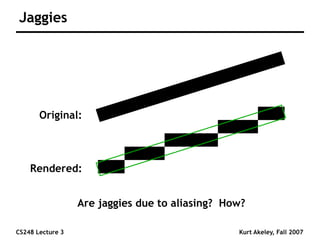
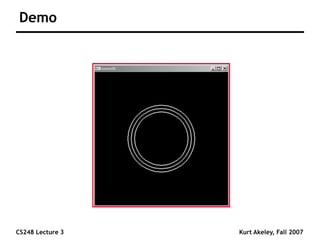
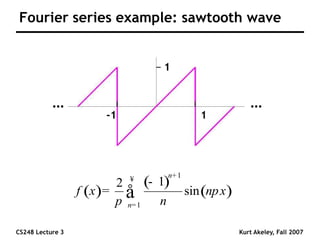
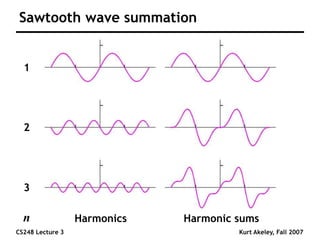
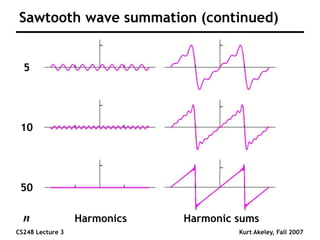
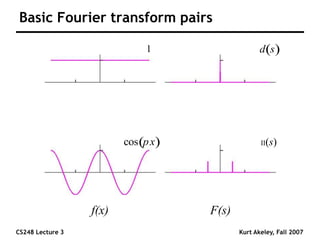
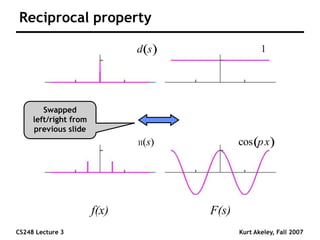
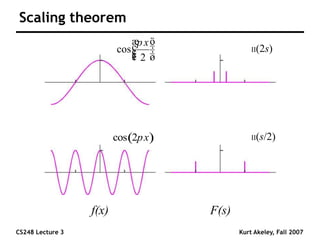
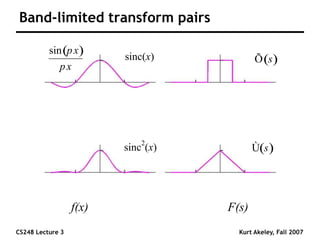
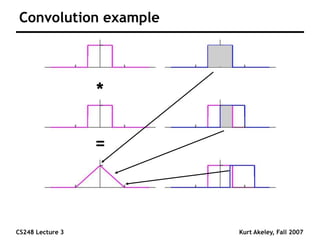
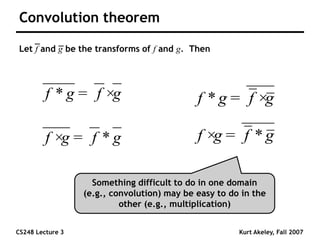
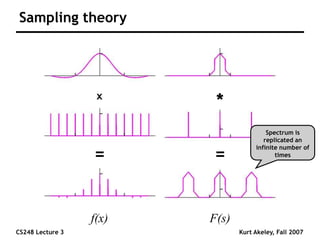
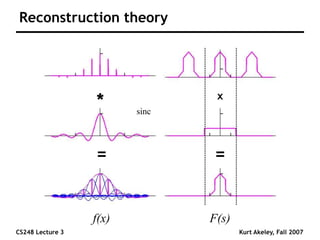
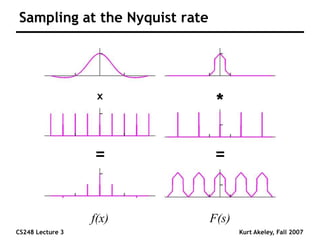
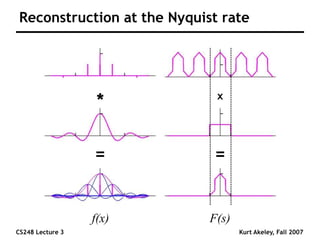
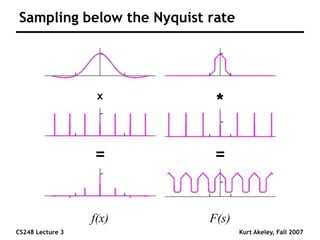
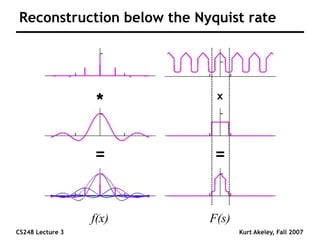
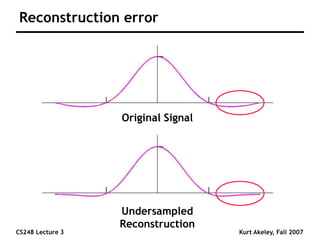
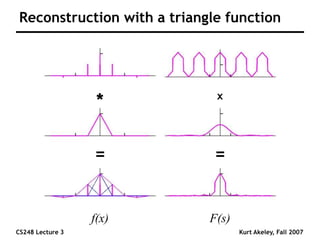
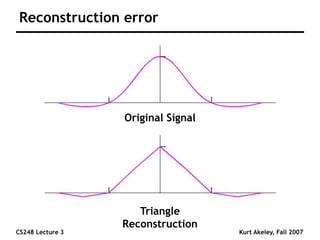
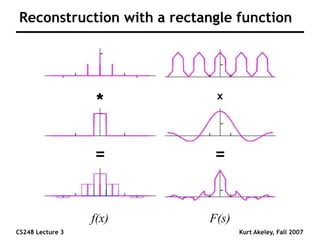
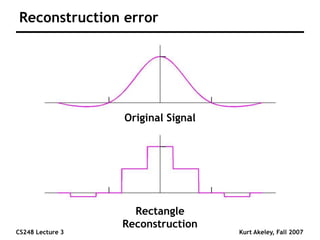
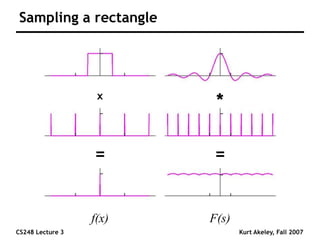
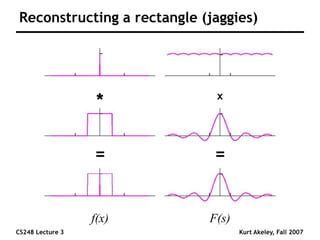
This document summarizes a lecture on sampling and aliasing in computer graphics. It discusses how aliasing occurs due to sampling signals below the Nyquist rate or using improper reconstruction methods. Specifically, it explains that "jaggies" in rendered images are a form of aliasing caused by undersampling high frequency components in the original image. The document also provides examples demonstrating how aliasing arises from sampling and reconstructing simple 1D signals, and how it can be avoided by sampling at or above the Nyquist rate and using sinc function reconstruction.

1. Sampling and Aliasing
Kurt Akeley
CS248 Lecture 3
2 October 2007
http://graphics.stanford.edu/courses/cs248-07/

2. CS248 Lecture 3 Kurt Akeley, Fall 2007
Aliasing
Aliases are low frequencies in a rendered
image that are due to higher frequencies
in the original image.

3. CS248 Lecture 3 Kurt Akeley, Fall 2007
Jaggies
Are jaggies due to aliasing? How?
Original:
Rendered:

4. CS248 Lecture 3 Kurt Akeley, Fall 2007
Demo

5. CS248 Lecture 3 Kurt Akeley, Fall 2007
What is a point sample (aka sample)?
An evaluation
 At an infinitesimal point (2-D)
 Or along a ray (3-D)
What is evaluated
 Inclusion (2-D) or intersection (3-D)
 Attributes such as distance and color

6. CS248 Lecture 3 Kurt Akeley, Fall 2007
Why point samples?
Clear and unambiguous semantics
Matches theory well (as we’ll see)
Supports image assembly in the framebuffer
 will need to resolve visibility based on distance,
and this works well with point samples
Anything else just puts the problem off
 Exchange one large, complex scene for many
small, complex scenes

7. CS248 Lecture 3 Kurt Akeley, Fall 2007
Fourier theory
“Fourier’s theorem is not only one of the most
beautiful results of modern analysis, but it
may be said to furnish an indispensable
instrument in the treatment of nearly every
recondite question in modern physics.”
-- Lord Kelvin

8. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reference sources
Marc Levoy’s notes
Ronald N. Bracewell, The Fourier Transform and its
Applications, Second Edition, McGraw-Hill, Inc.,
1978.
Private conversations with Pat Hanrahan
MATLAB

9. CS248 Lecture 3 Kurt Akeley, Fall 2007
Ground rules
You don’t have to be an engineer to get this
 We’re looking to develop instinct / understanding
 Not to be able to do the mathematics
We’ll make minimal use of equations
 No integral equations
 No complex numbers
Plots will be consistent
 Tick marks at unit distances
 Signal on left, Fourier transform on the right

10. CS248 Lecture 3 Kurt Akeley, Fall 2007
Dimensions
1-D
 Audio signal (time)
 Generic examples (x)
2-D
 Image (x and y)
3-D
 Animation (x, y, and time)
All examples in this presentation are 1-D

11. CS248 Lecture 3 Kurt Akeley, Fall 2007
Fourier series
Any periodic function can be exactly
represented by a (typically infinite) sum
of harmonic sine and cosine functions.
Harmonics are integer multiples of the
fundamental frequency

12. CS248 Lecture 3 Kurt Akeley, Fall 2007
Fourier series example: sawtooth wave
…
…
( )
( )
( )
1
1
1
2
sin
n
n
f x n x
n
p
p
+
¥
=
-
= å
1
1
-1

13. CS248 Lecture 3 Kurt Akeley, Fall 2007
Sawtooth wave summation
Harmonics Harmonic sums
1
2
3
n

14. CS248 Lecture 3 Kurt Akeley, Fall 2007
Sawtooth wave summation (continued)
Harmonics Harmonic sums
5
10
50
n

15. CS248 Lecture 3 Kurt Akeley, Fall 2007
Fourier integral
Any function (that matters in graphics)
can be exactly represented by an
integration of sine and cosine functions.
Continuous, not harmonic
But the notion of harmonics will
continue to be useful

16. CS248 Lecture 3 Kurt Akeley, Fall 2007
Basic Fourier transform pairs
1 ( )
s
d
f(x) F(s)
( )
cos x
p II(s)

17. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reciprocal property
Swapped
left/right from
previous slide
f(x) F(s)
1
( )
cos x
p
( )
s
d
II(s)

18. CS248 Lecture 3 Kurt Akeley, Fall 2007
Scaling theorem
( )
cos 2 x
p
cos
2
x
p
æ ö
÷
ç ÷
ç ÷
ç
è ø
II(2s)
II(s/2)
f(x) F(s)

19. CS248 Lecture 3 Kurt Akeley, Fall 2007
Band-limited transform pairs
( )
s
Ù
F(s)
f(x)
sinc(x)
( )
sin x
x
p
p
( )
s
Õ
sinc
2
(x)

20. CS248 Lecture 3 Kurt Akeley, Fall 2007
Finite / infinite extent
If one member of the transform pair is finite, the other
is infinite
 Band-limited  infinite spatial extent
 Finite spatial extent  infinite spectral extent

21. CS248 Lecture 3 Kurt Akeley, Fall 2007
Convolution
( ) ( ) ( ) ( )
f x g x f u g x u du
¥
- ¥
* = -
ò

22. CS248 Lecture 3 Kurt Akeley, Fall 2007
Convolution example
*
=

23. CS248 Lecture 3 Kurt Akeley, Fall 2007
Convolution theorem
Let f and g be the transforms of f and g. Then
f g f g
* = ×
f g f g
× = *
f g f g
* = ×
f g f g
× = *
Something difficult to do in one domain
(e.g., convolution) may be easy to do in the
other (e.g., multiplication)

24. CS248 Lecture 3 Kurt Akeley, Fall 2007
Sampling theory
x
=
*
=
F(s)
f(x)
Spectrum is
replicated an
infinite number of
times

25. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reconstruction theory
x
=
*
=
F(s)
f(x)
sinc

26. CS248 Lecture 3 Kurt Akeley, Fall 2007
Sampling at the Nyquist rate
x
=
*
=
F(s)
f(x)

27. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reconstruction at the Nyquist rate
x
=
*
=
F(s)
f(x)

28. CS248 Lecture 3 Kurt Akeley, Fall 2007
Sampling below the Nyquist rate
x
=
*
=
F(s)
f(x)

29. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reconstruction below the Nyquist rate
x
=
*
=
F(s)
f(x)

30. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reconstruction error
Original Signal
Undersampled
Reconstruction

31. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reconstruction with a triangle function
x
=
*
=
F(s)
f(x)

32. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reconstruction error
Original Signal
Triangle
Reconstruction

33. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reconstruction with a rectangle function
x
=
*
=
F(s)
f(x)

34. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reconstruction error
Original Signal
Rectangle
Reconstruction

35. CS248 Lecture 3 Kurt Akeley, Fall 2007
Sampling a rectangle
x
=
*
=
F(s)
f(x)

36. CS248 Lecture 3 Kurt Akeley, Fall 2007
Reconstructing a rectangle (jaggies)
x
=
*
=
F(s)
f(x)

37. CS248 Lecture 3 Kurt Akeley, Fall 2007
Sampling and reconstruction
Aliasing is caused by
 Sampling below the Nyquist rate,
 Improper reconstruction, or
 Both
We can distinguish between
 Aliasing of fundamentals (demo)
 Aliasing of harmonics (jaggies)

38. CS248 Lecture 3 Kurt Akeley, Fall 2007
Summary
Jaggies matter
 Create false cues
 Violate rule 1
Sampling is done at points (2-D) or along rays (3-D)
 Sufficient for depth sorting
 Matches theory
Fourier theory explains jaggies as aliasing. For correct
reconstruction:
 Signal must be band-limited
 Sampling must be at or above Nyquist rate
 Reconstruction must be done with a sinc function

39. CS248 Lecture 3 Kurt Akeley, Fall 2007
Assignments
Before Thursday’s class, read
 FvD 3.17 Antialiasing
Project 1:
 Breakout: a simple interactive game
 Demos Wednesday 10 October

40. CS248 Lecture 3 Kurt Akeley, Fall 2007
End