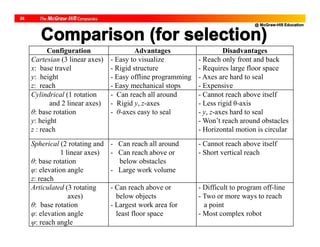
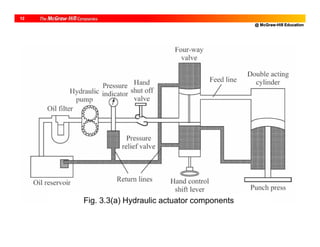
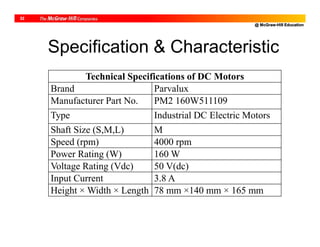
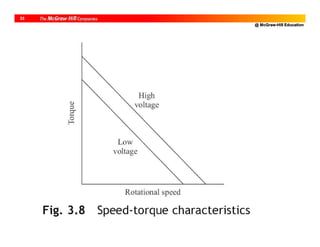
The document discusses different types of actuators used in robotics, including pneumatic, hydraulic, and electric actuators. Pneumatic actuators use compressed air and have advantages of low cost and easy control but lack precision. Hydraulic actuators can apply large forces with high power-to-size ratios but require complex servo control and have risks of leakage and fire. Electric actuators are now most common and include stepper motors for position control and DC motors for applications requiring higher power and torque control. The document compares characteristics of different actuator types for robotic applications.

![Laws of Robotics
• A robot must not harm a human being, nor
through inaction allow one to come to harm.
• A robot must always obey human beings,
unless that is in conflict with the 1st law.
• A robot must protect from harm, unless that is
in conflict with the 1st two laws.
• A robot may take a human being’s job but it
may not leave that person jobless. [Fuller(1999)]](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-2-320.jpg)

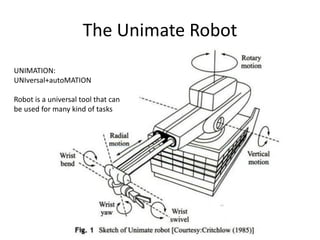
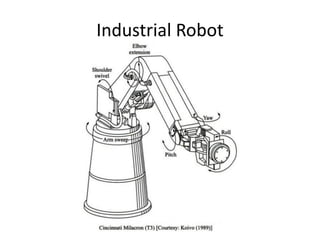



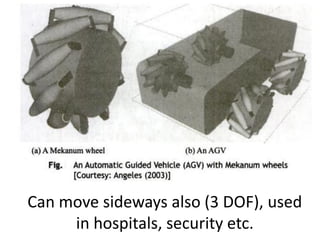
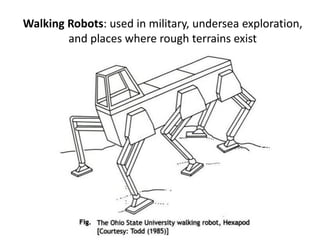






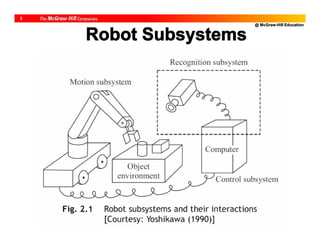



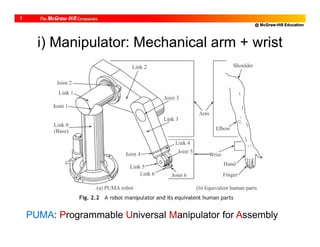
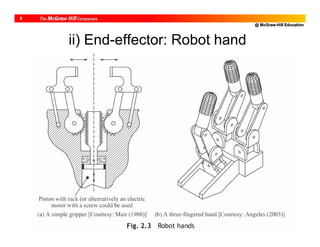

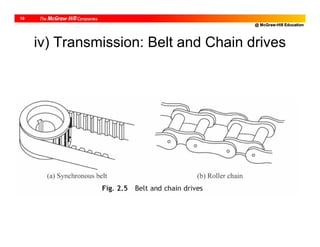
![@ McGraw-Hill Education
13
Recognition Subsystem
(ii) Analog-to-Digital
Converter (ADC)
- Electronic device
(i) Sensors (Essentially transducers)
- Converts a signal
to another
Fig. 2.8 An analog-to-digital converter
[Courtesy: http://www.eeci.com/adc-16p.htm]](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-27-320.jpg)
![@ McGraw-Hill Education
14
Control Subsystem
(i) Digital Controller
- CPU, Memory, Hard disk (to store programs)
Controller
Robot
Sensor
Desired end-effector
trajectory
Driving
input
Actual end-effector
configuration
Joint displacement
and velocity
Fig. 2.9 Control subsystem
[Courtesy: http://www.abb.com/Product/seitp327/f0cec80774b0b3c9c1256fda00409c2c.aspx]
(a) Control scheme of a robot (b) ABB Controller](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-28-320.jpg)
![@ McGraw-Hill Education
15
Control Subsystem (contd.)
(ii) Digital-to-Analog Converter (DAC)
(iii) Amplifier
- Amplify weak commands from DAC
Fig. 2.10 A digital-to-analogue converter
[Courtesy: http://www.eeci.com]](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-29-320.jpg)



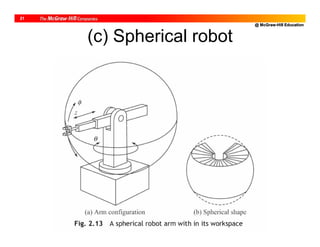
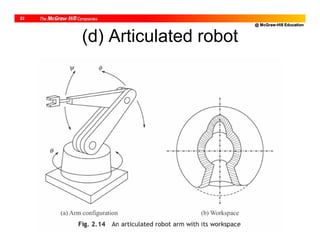
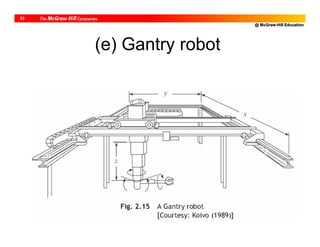
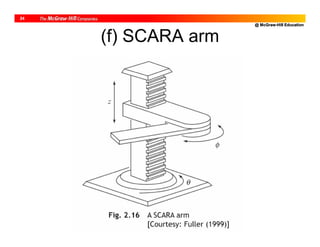









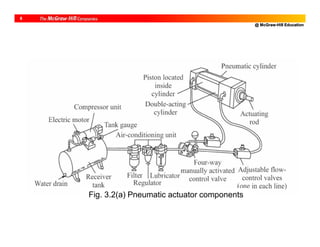
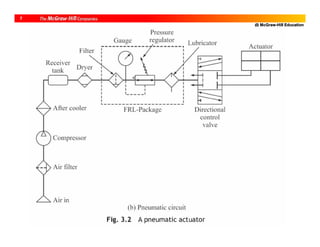
![@ McGraw-Hill Education
5
• One of fluid devices
• Uses compressed air [1-7 bar; ~.1 MPa/bar]
• Components
1) Compressor; 2) After-cooler; 3) Storage tank;
4) Desiccant driers; 5) Filters; 6) Pressure
regulators; 7) Lubricants; 8) Directional control
valves; 9) Actuators
Pneumatic Actuators](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-49-320.jpg)




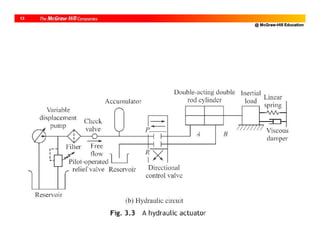








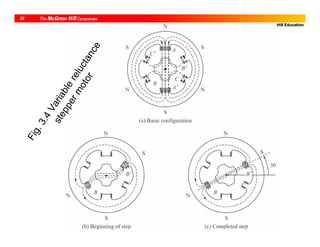

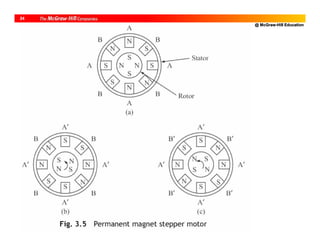



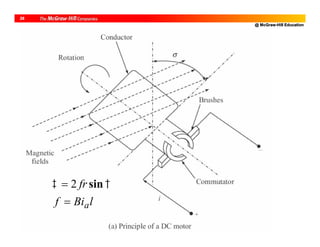

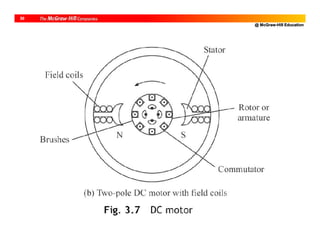

![@ McGraw-Hill Education
34
Permanent Magnet (PM) Motor
• Two configurations
– Cylindrical [Common in industrial robots]
– Disk](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-78-320.jpg)
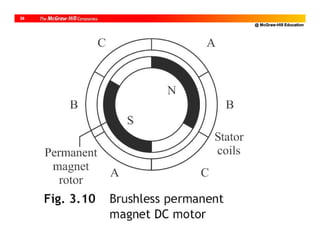
![@ McGraw-Hill Education
35
Permanent Magnet (PM) Motor (cont.)
• No field coils
• Field is by permanent magnets (PM)
• Some PM has coils for recharge
• Torque Armature current [Const. flux]](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-79-320.jpg)







![@ McGraw-Hill Education
46
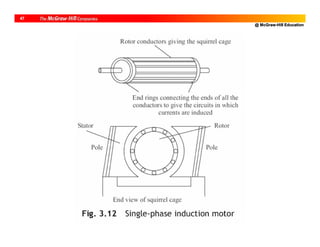
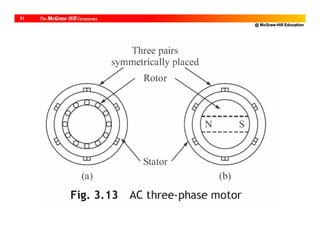
Classification of an AC Motor
• Single-phase [Low-power requirements]
– Induction
– Synchronous
• Poly-phase (typically 3-phase) [High-
power requirements]
– Induction
– Synchronous
• Induction motors are cheaper Widely
used](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-90-320.jpg)











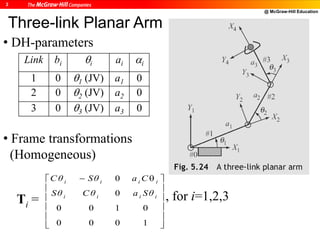













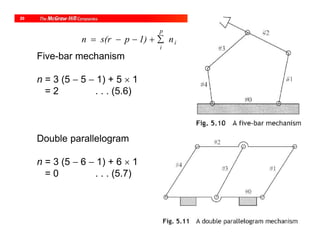



![@ McGraw-Hill Education
24
xp
zp
ypF][p . . . (5.8)
[ ] , [ ] , and [ ]
1 0 0
0 1 0
00 1
F F Fx y z
. . . (5.10)
Position Description
p = px x + py y + pz z . . . (5.9)](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-133-320.jpg)


![@ McGraw-Hill Education
27
p = (puux + pvvx + pwwx)x + (puuy + pvvy + pwwy)y
+ (puuz + pvvz + pwwz)z . . . (5.13)
px = uxpu + vxpv + wxpw . . . (5.14a)
py = uypu + vypv + wypw . . . (5.14b)
pz = uzpu + vzpv + wzpw . . . (5.14c)
Substitute eqs. (5.11a-c) into eq. (5.12)
[p]F = Q [p]M . . . (5.15)](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-136-320.jpg)
![@ McGraw-Hill Education
28
[p]F = Q [p]M . . . (5.15)
xwxvxu
zwzvzu
ywyvyuQpp
TTT
TTT
TTT,][,][
x
w
x
v
x
u
z
w
z
v
z
u
y
w
y
v
y
u
F
u
p
w
p
v
p
x
p
z
p
y
p M
.. . (5.16)
uTu = vTv = wTw = 1, and
uTv(vTu) = uTw(wTu) = vTw(wTv) = 0 … (5.17)
Q is called Orthogonal](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-137-320.jpg)

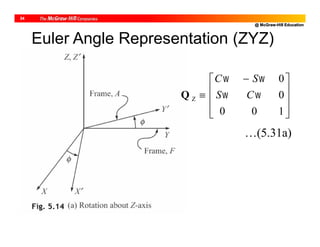
![@ McGraw-Hill Education
30
[ ,
[ ] ,
[ ]
0
0
0
0
1
u]
v
w
F
F
F
Cα
Sα
Sα
Cα
. . . (5.20)
Example 5.6 Elementary Rotations (Fig. 5.13a)](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-139-320.jpg)

![@ McGraw-Hill Education
32
pz = pw . . . (5.25)
[p]F = QZ [p]M . . . (5.26)
py = pu S + pv C . . . (5.24)
px = pu C pv S . . . (5.23)
Example 5.8 Coordinate Transformation (Fig. 5.13b)](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-141-320.jpg)
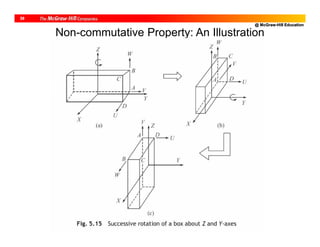
![@ McGraw-Hill Education
33
px = px C py S . . . (5.27)
py = px S + py C . . . (5.28)
pz = pz . . . (5.29)
Example 5.9 Vector Rotation (Fig. 5.13c)
[p]F = QZ [p]F … (5.30)](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-142-320.jpg)







![@ McGraw-Hill Education
43
p = o + p . . . (5.34)
[p]F = [o]F + Q[p’]M . . . (5.35)
1
][
1
][
1
][
T
F MF poQp
0
. . . (5.36)
MF ][][ pTp . . . (5.37)
Homogenous Transformation](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-152-320.jpg)
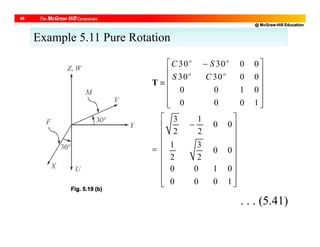
![@ McGraw-Hill Education
44
TTT 1 or T1 TT . . . (5.38)
1
][
T
TT
1
0
oQQ
T F
. . . (5.39)
1000
1100
2010
0001
T
. . . (5.40)
Example 5.10 Pure Translation
T: Homogenous transformation matrix (4 4)
Fig. 5.19 (a)](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-153-320.jpg)


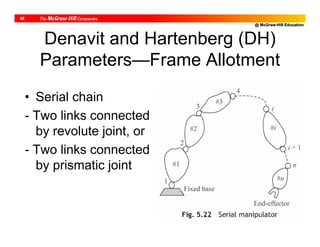
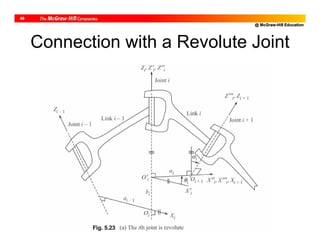
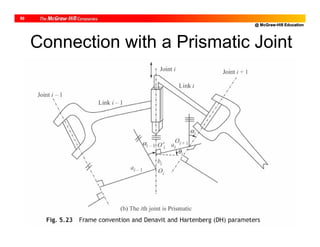

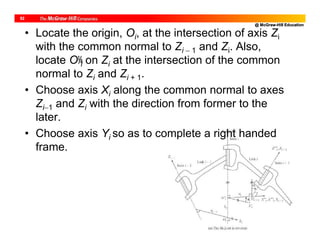



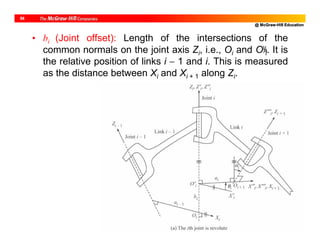
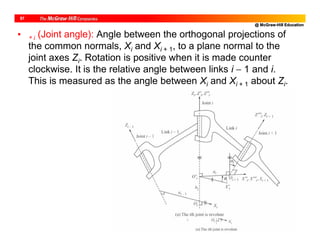
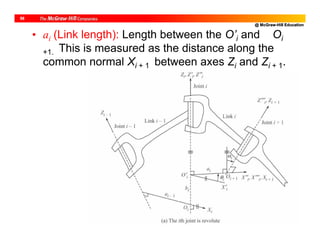
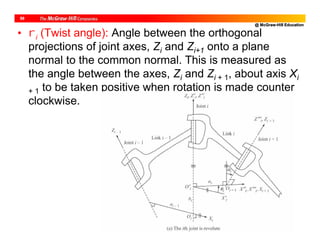

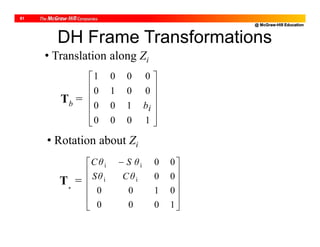



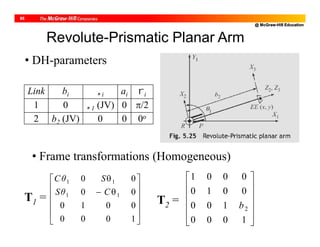
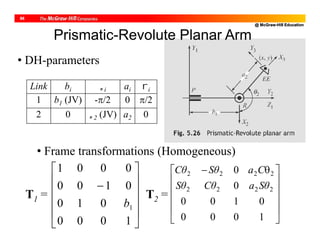





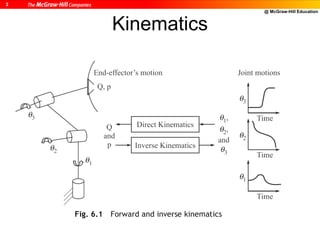



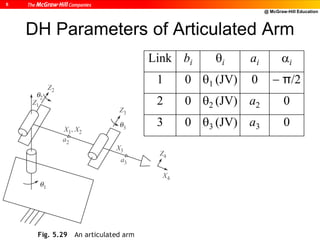


![@ McGraw-Hill Education
10
DH Parameters of PUMA Robot
i bi i ai i
1 0 1 (JV) [0] 0 -/2
2 b2 2 (JV) [-/2] a2 0
3 0 3 (JV) [/2] a3 /2
4 b4 4 (JV) [0] 0 -/2
5 0 5 (JV) [0] 0 /2
6 b6 6 (JV) [0] 0 0](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-189-320.jpg)

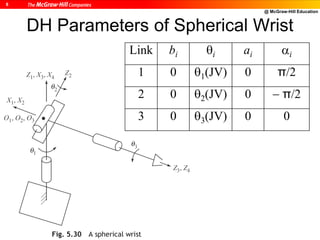
![@ McGraw-Hill Education
12
DH Parameters of Stanford Arm
i bi i ai i
1 b1 1 (JV) [0] 0 -/2
2 b2 2 (JV) [] 0 -/2
3 b3
(JV)
0 0 0
4 b4 4 (JV) [0] 0 /2
5 0 5 (JV) [0] 0 -/2
6 0 6 (JV) [0] 0 0](https://image.slidesharecdn.com/roboticsdone-171104154009/85/Robotics-done-191-320.jpg)