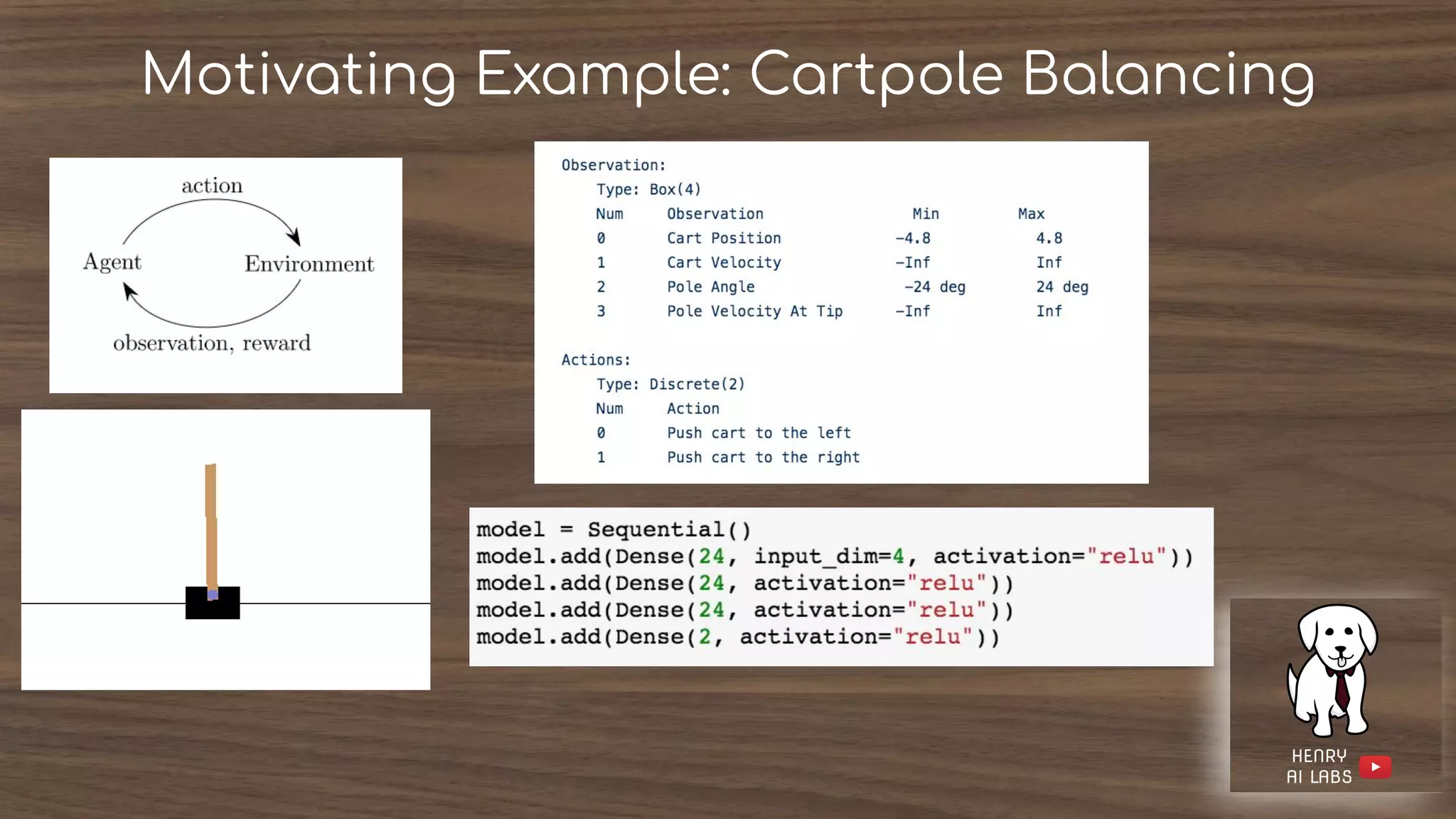
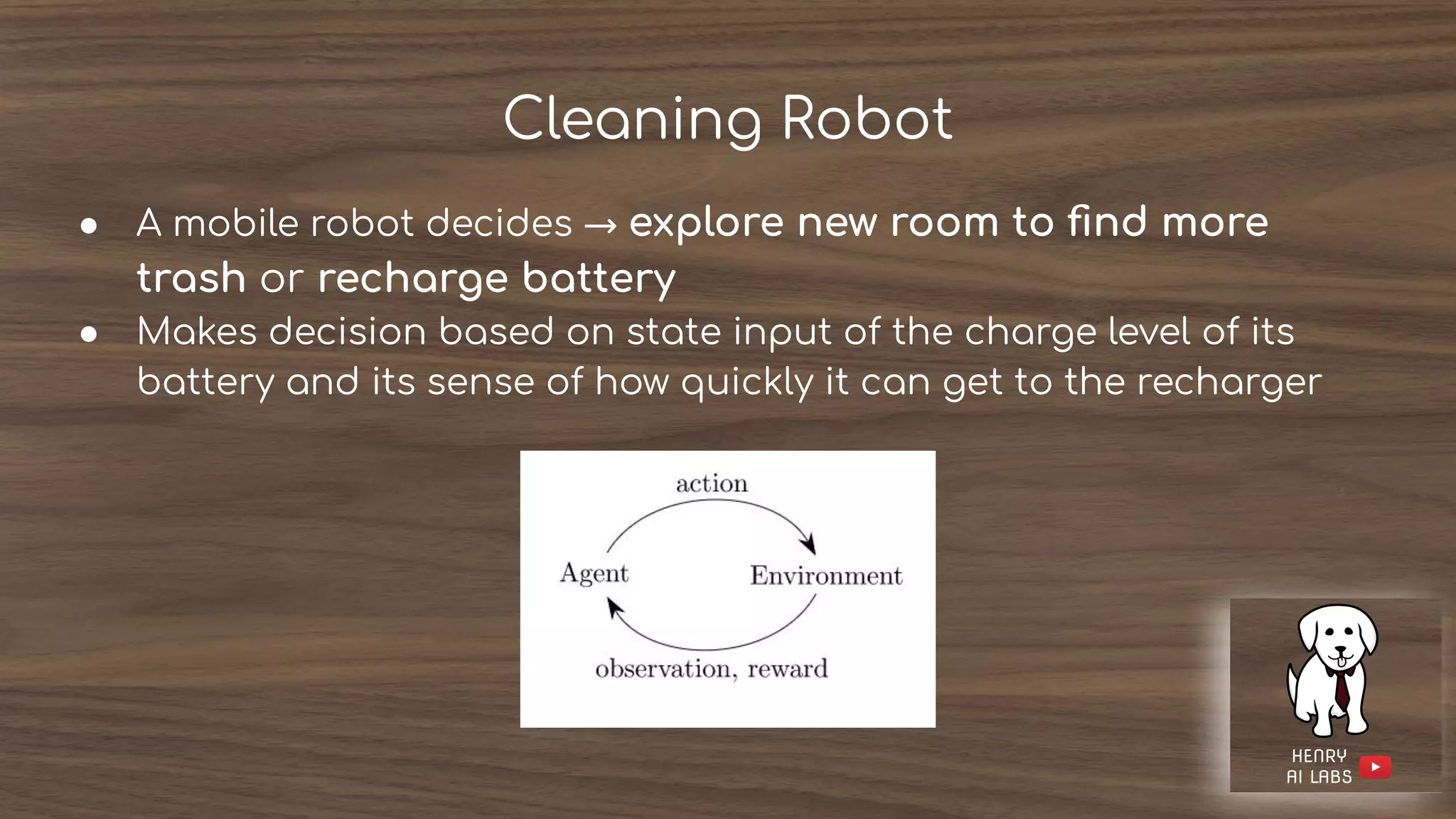
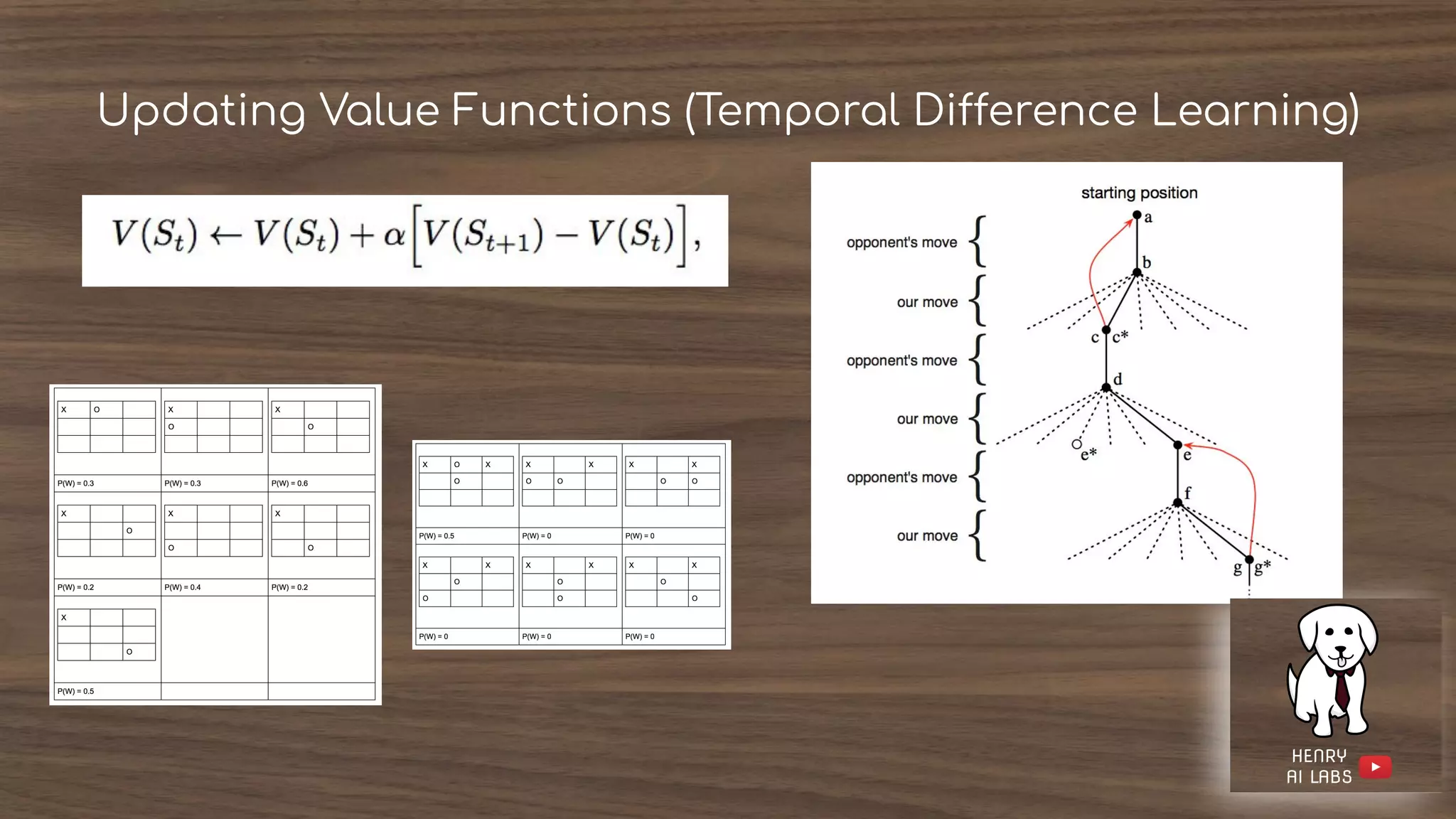
The document introduces reinforcement learning (RL) by discussing its core components: policies, rewards, value functions, and optional models. It highlights key challenges such as exploration versus exploitation and the importance of estimating values for effective decision-making. Examples of RL applications, including games and adaptive systems, illustrate the complexity and utility of RL in real-world scenarios.

1. Chapter 1: Introduction
Richard S. Sutton and Andrew G. Barto

2. Reinforcement Learning:
A Computational Approach to
Learning from Interaction with an
Environment
Policies
Value Functions
Rewards
Models

3. Motivating Example: Cartpole Balancing

4. Mapping State to Actions to
Maximize a Reward Signal

5. Key Challenges to RL:
1. Search: Exploration-Exploitation
2. Delayed Reward
- Agents must consider more than the immediate
reward because acting greedily like this may
result in less future reward

6. Exploration-Exploitation
● To obtain a lot of reward, a reinforcement learning agent must
prefer actions that it has tried in the past and found to be
effective in producing reward
● But to discover such actions, it has to try actions that it has not
selected before

7. Exploration-Exploitation
● Exploit (act greedily) w.r.t it has already experienced to maximize reward
● Explore (act non-greedily) take actions which don’t have the maximum expected
reward in order to learn more about them and make better selections in the
future
● Stochastic Tasks, each action must be tried many times to gain a reliable
estimate of its expected reward

8. 4 Key Elements of Reinforcement Learning
● Policy
● Reward
● Value Function
● Model (Optional)

9. Policy
● This is the mapping from states to actions
● Defining the agent’s behavior
● Policies are usually stochastic, meaning that we sample an action from a
probability distribution compared to something like supervised learning
where we would take the argmax of the distribution

10. Reward
● Goal of the RL agent
● The environment sends a reward at each time step (usually 0)
● Agent is trying to maximize reward
● Primary basis for altering the policy
○ (Also Novelty Search / Intrinsic Motivation)
● Reward signals may be stochastic functions of state and actions

11. Value Function
● Assigning values to states
● Specifies what is good in the long run vs. reward which is an immediate signal
● The value of a state is the reward the agent can expect starting from that state
● Values correspond to a more refined and farsighted judgment of how pleased
or displeased we are that our environment is in a particular state

12. Model (Optional → Model-Based vs. Model-Free)
● Mimics the behavior of the environment
● Allows inference about how the environment might behave
● Given a state and action, the model might predict the resultant
next state and next reward
● Models are used for planning, considering future situations
before experiencing them
● Model-Based (Models and Planning)
● Model-Free (Explicitly Trial-and-Error Learners)

13. Reinforcement vs. Supervised Learning
● Supervised Learning tells the agent the exact correct situation for every state
for the purpose of generalizing to states not seen in the training set
● Reinforcement Learning generally has a much sparser reward signal, do not
know what the correct action for every state is, but receive rewards based on a
series of states and actions

14. Examples of
Reinforcement Learning

15. Chess
● A Move is informed by planning (anticipating possible responses and
counter-responses) and judgments of particular positions and moves

16. Petroleum Refinery
● An adaptive controller adjusts parameters of a petroleum
refinery’s operation in real time
● Optimizes a reward function of yield/cost/quality without sticking
strictly to the set points originally suggested by engineers
Really good example of this is DeepMind / Google Data Center Cooling Bill reduction by 40% (Link in Description)

17. Gazelle Calf
● Struggles to its feet minutes after being born
● Half an hour later, it is running at 20 miles per hour

18. Cleaning Robot
● A mobile robot decides → explore new room to find more
trash or recharge battery
● Makes decision based on state input of the charge level of its
battery and its sense of how quickly it can get to the recharger

19. Phil Making Breakfast
● Closely examined, contains a complex web of behavior and
interlocking goal-subgoal relationships
● Walk to cupboard, open it, select a cereal box, reach for it, grasp it,
retrieve the box
● Each step is guided by goals and is in service of other goals
“grasping a spoon”

20. The Agent seeks to achieve a goal
despite uncertainty about its
environment

21. Actions change future states
● Chess moves
● Levels of reservoirs of the refinery
● Robot’s next location and charge level of its battery
→ Impacting actions available to the agent in the future

22. Goals explicit in the sense that the agent can
judge progress toward it goal based on what it
can sense directly
● Chess player knows whether or not he wins
● The refinery controller knows how much petroleum is being
produced
● The gazelle calf knows when it falls
● The mobile robot knows when its batteries run down
● Phil knows whether or not he is enjoying his breakfast

23. Rewards are given directly by the environment,
but values must be estimated and re-estimated
from the sequences of observations an agent
makes over its entire lifetime

24. The most important component of all RL
algorithms is method for efficiently estimating
values
The central role of value estimation is arguably
the most important breakthrough in RL over the
last 6 decades

25. Evolutionary Methods and RL
● Apply multiple static policies with separate instances of the
environment
● Policies obtaining the most reward carried over to the next
generation of policies
● Skips estimating value functions in the process

26. Evolutionary Methods ignore crucial information
● The frequency of wins gives an estimate of the probability of winning with that policy,
used to direct the next policy selection
● What happens during the game is ignored
→ If the player wins, all of its behavior in the game is given credit
● Value function methods allow individual states to be evaluated
● Learning a value function takes advantage of information available during the
course of play

27. Tic-Tac-Toe against an imperfect player
● The policy describes the move to make given the state of the board
● Value Function → An estimate of winning probability for each state could be obtained by
playing the game many times
● State A has higher value than state B if the current winning estimate is higher from A than B

28. Tic-Tac-Toe
● Most of the time we move greedily, selecting the action that leads
to the state with the greatest value
● Exploratory moves → Select randomly despite what the value
function would prefer
● Update values of states throughout experience

29. Updating Value Functions (Temporal Difference Learning)

30. Lessons learned from Tic-Tac-Toe
● Tic-tac-toe has a relatively small, finite state set
● Compared with backgammon ~1020
states
● This many states makes it impossible to experience more than a small fraction
of them
● The artificial neural network provides the program with the ability to generalize
from its experience so that in new states it selects moves based on information
saved from similar states faced in the past

31. Self-Play
● What if the agent played against itself with both sides learning?
● Would it learn a different policy for selecting moves?

32. Symmetries
● Many tic-tac-toe positions appear different but are really the same because of
symmetries. How might we amend the learning process described above to take
advantage of this?
● In what ways would this change improve the learning process?
● Suppose the opponent did not take advantage of symmetries.
● Is it true then, that symmetrically equivalent positions should have the same value?

33. Greedy Play
● Suppose the RL player was greedy, it always played the move that
brought it to the position that it rated the best.
● Might it learn to play better, or worse, than a non-greedy player?
What problems might occur?

34. Learning from Exploration
● Suppose learning updates occurred after all moves, including exploratory moves.
● If the step-size parameter is appropriately reduced over time (but not the tendency
to explore), then the state values would converge to a different set of probabilities.
● What are the two sets of probabilities computed when we do and when we do not
learn from exploratory moves?
● Assuming that we do continue to make exploratory moves, which set of probabilities
might be better to learn? Which would result in more wins?

35. Reinforcement Learning
Chapter 1
Policies
Value Functions
Rewards
Models