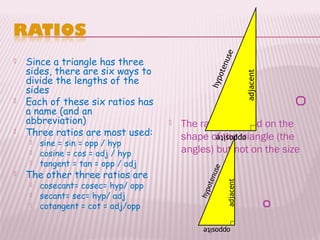
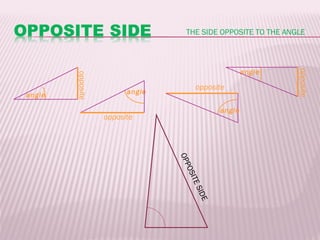
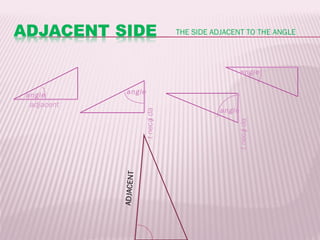
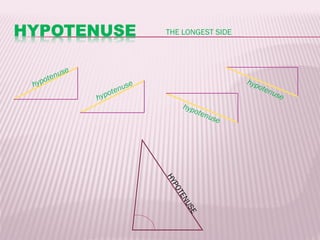
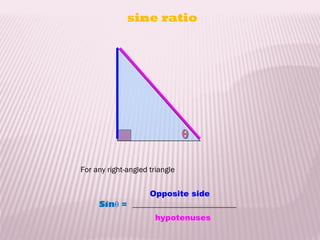
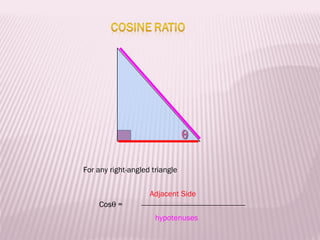
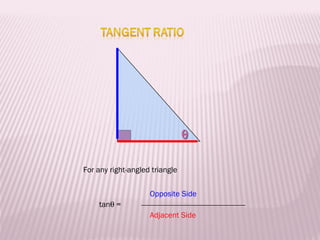
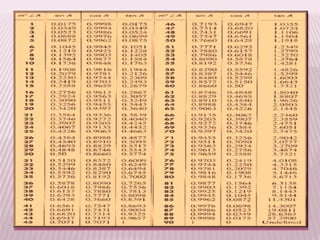
This document discusses trigonometric ratios and identities. It defines the three main trigonometric ratios - sine, cosine, and tangent - as ratios of the lengths of sides of a right triangle. It also introduces six trigonometric functions defined as reciprocals or quotients of the main ratios. The document provides examples of using trigonometric identities to verify relationships between functions through algebraic manipulation.

1. Made by:
BHAVUN CHHABRA
10TH - B

2.  Trigonometry is the study and solution of
Triangles. Solving a triangle means finding
the value of each of its sides and angles.
The following terminology and tactics will be
important in the solving of triangles.
Pythagorean Theorem (a2+b2=c2). Only for right angle
triangles
Sine (sin), Cosecant (csc or sin-1)
Cosine (cos), Secant (sec or cos-1)
Tangent (tan), Cotangent (cot or tan-1)
Right/Oblique triangle

3. us e
 Since a triangle has three
ten
sides, there are six ways to
adjacent
o
divide the lengths of the
hyp
sides
 Each of these six ratios has
a name (and an
abbreviation)  The ratios depend on the
 Three ratios are most used: shape of the triangle (the
opposite
 sine = sin = opp / hyp
 cosine = cos = adj / hyp angles) but not on the size
 tangent = tan = opp / adj
e
The other three ratios are
nus

ote
adjacent
 cosecant= cosec= hyp/ opp
hyp
 secant= sec= hyp/ adj
 cotangent = cot = adj/opp
opposite

5. THE SIDE OPPOSITE TO THE ANGLE
angle
opposite
opposite
opposite
angle angle
angle
opposite
OP
PO
SIT
E SID
E

6. THE SIDE ADJACENT TO THE ANGLE
angle
angle angle
adjacent
angle
t nec a da
t nec a da
j
j
ADJACENT

7. THE LONGEST SIDE
se
enu
hy pot e h yp
e nus ote
nu
hy pot se
hyp
o te n
use
HY
PO
TE
NU
SE

8. THREE TYPES TRIGONOMETRIC
RATIOS
There are 3 kinds of trigonometric ratios
we will learn.
sine ratio
cosine ratio
tangent ratio

9. sine ratio
θ
For any right-angled triangle
Opposite side
Sinθ =
hypotenuses

10. θ
For any right-angled triangle
Adjacent Side
Cosθ =
hypotenuses

11. θ
For any right-angled triangle
Opposite Side
tanθ =
Adjacent Side

13. Reciprocal Identities
1 1 1
cot θ = secθ = cscθ =
tan θ cosθ sin θ
Quotient Identities
sin θ cosθ
tan θ = cot θ =
cosθ sin θ
Pythagorean Identities
sin θ + cos θ = 1 tan θ + 1 = sec θ 1 + cot θ = csc θ
2 2 2 2 2 2
Negative-Number Identities
sin( −θ ) = − sin θ cos( −θ ) = cosθ tan( −θ ) = − tan θ

14.  Work with one side at a time.
 We want both sides to be exactly the same.
 Start with either side
 Use algebraic manipulations and/or the basic
trigonometric identities until you have the same
expression as on the other side.

15. cot x sin x = cos x
LHS = cot x sin x
and RHS = cos x
cos x
= ⋅ sin x
sin x
= cos x
Since both sides are the same, the identity is verified.

16.  Start with the more complicated side
 Try substituting basic identities (changing all functions to be
in terms of sine and cosine may make things easier)
 Try algebra: factor, multiply, add, simplify, split up fractions
 If you’re really stuck make sure to:
Change everything on both sides to
sine and cosine.