Download to read offline
Vectors.pptx
- 1.
- 2. Vectors Vectors aredefined as mathematical expressions possessing magnitude and direction, which add according to the parallelogram law P P Equal vectors have the same magnitude and direction even if they have different points of application The negative of a vector has the same magnitude but opposite direction of the given vector P -P
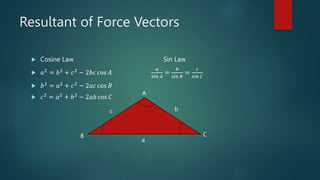
- 3. Addition of Vectors Vectors can be added according to parallelogram law or triangle rule A Q P P Q Using parallelogram law to add two vectors The triangle rule of vectors addition
- 4. Addition of Vectors3 or more The sum of two or more vectors can be found by arranging all the vectors in a tip –to – tail fashion and then connecting the tail of the first vector to the tip of the last vector A Q S
- 5. PRODUCT OF SCALARAND VECTOR Multiplying a vector by a scalar changes the vector’s magnitude but not its direction. P 1.5P -2P
- 6. Resultant of SeveralConcurrent Forces Consider a particle A acted upon several coplanar forces. Since the forces all pass through A, the forces are said to concurrent. The single force R has the same effect on particle A which is called the resultant. Q P A S A Q Q P S R Concurrent forces can be added by the polygon rule
- 7. Resultant of ForceVectors Cosine Law Sin Law 𝑎2 = 𝑏2 + 𝑐2 − 2𝑏𝑐 cos 𝐴 𝑎 sin 𝐴 = 𝑏 sin 𝐵 = 𝑐 sin 𝐶 𝑏2 = 𝑎2 + 𝑐2 − 2𝑎𝑐 cos 𝐵 𝑐2 = 𝑎2 + 𝑏2 − 2𝑎𝑏 cos 𝐶 B A C a c b
- 8. Sample Problem Twoforces P and Q act on a bolt A. Determine the resultant
- 10. Adding Forces byComponents A force F can be resolved into a component Fx along the x-axis and a component Fy along the y-axis Fx Fy x y 0 ∅ y Rectangular components of a force F Rectangular components of a force F for axes-rotated away from horizontal and vertical