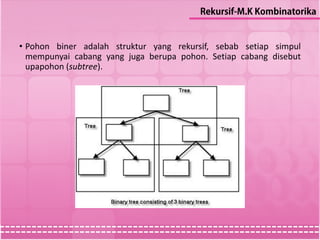
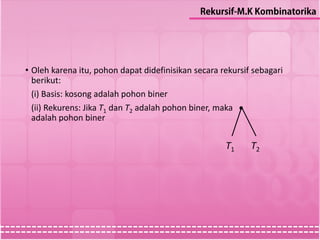
Dokumen ini menjelaskan konsep rekursi dan definisinya dalam bahasa pemrograman, termasuk langkah-langkah mendefinisikan objek, barisan, fungsi, dan himpunan secara rekursif. Contoh yang diberikan meliputi barisan bilangan pangkat dari 2, fungsi Fibonacci, dan himpunan bilangan positif yang habis dibagi 3. Selain itu, dijelaskan juga induksi struktural sebagai metode untuk membuktikan sifat-sifat dari himpunan yang didefinisikan secara rekursif.

1. • Oleh :
• Wulan Resti Oktaviani
• 90115010

2. REKURSI
Definisi
Rekursi
Induksi
Struktural

3. Pengantar Rekursi
• Ada kalanya kita mengalami kesulitan untuk mendefinisikan suatu
obyek secara eksplisit.
• Proses mendefinisikan objek tersebut dengan menggunakan dirinya
sendiri disebut rekursi (recursion).
• Kita dapat mendefinisikan barisan, fungsi dan himpunan secara
rekursif.

4. Definisi Gambar Rekursi
Gambar 1. Definisi Gambar Rekursi

5. Gambar 2. Definisi Gambar Rekursi

6. Barisan yang didefinisikan secara Rekursif
Contoh:
Barisan bilangan pangkat dari 2
an = 2n untuk n = 0, 1, 2, … .
Barisan ini dapat didefinisikan secara rekursif:
a0 = 1
an+1 = 2an untuk n = 0, 1, 2, …
Langkah-langkah untuk mendefinisikan barisan secara rekursif:
1. Langkah basis: Spesifikasi anggota awal.
2. Langkah rekursif: Berikan aturan untuk membangun anggota baru dari
anggota yang telah ada.

7. Contoh Barisan yang didefinisikan secara
Rekursif
Berikan definisi rekursif dari an=rn, dengan rN, r≠0 dan n bilangan
bulat positif.
Solusi:
Definisikan a0=r0=1
dan an+1=r . an untuk n = 0, 1, 2, …

8. Fungsi yang didefinisikan secara Rekursif
Langkah-langkah untuk mendefinisikan fungsi dengan domain bilangan
cacah:
1. Langkah basis: Definisikan nilai fungsi pada saat nol.
2. Langkah rekursif: Berikan aturan untuk mencari nilai fungsi untuk
setiap bilangan bulat berdasarkan nilai fungsi pada bilangan bulat
yang lebih kecil.
Definisi seperti itu disebut rekursif atau definisi induktif.

9. Contoh Fungsi yang di definisikan secara
rekursif (1)
f(0) = 3
f(n + 1) = 2f(n) + 3
Maka
f(0) = 3
f(1) = 2f(0) + 3 = 23 + 3 = 9 f(2) =
2f(1) + 3 = 29 + 3 = 21
f(3) = 2f(2) + 3 = 221 + 3 = 45
f(4) = 2f(3) + 3 = 245 + 3 = 93






0,3)1(2
0,3
)(
nnf
n
nf
basis
rekurens

10. Contoh Fungsi yang di definisikan secara
rekursif (2)
• Diberikan definisi rekursif , an dengan adalah bilangan real tak nol
dan bilangan bulat tak negatif
Solusi :
Definisi rekursif terdiri dari 2 langkah:
1) basis : spesifikasi anggota awal
a0 = 1
2) Rekursi : an
an+1 = a. an untuk n = 0,1,2,3,…
a
a

11. Contoh Fungsi yang di definisikan secara
rekursif (3)


n
k
kanf
0
)(
Bagaimana kita dapat mendefinisikan fungsi
secara rekursif?

12. n
n
k
k
nn
nn
n
k
k
aa
aaaaa
aaaaaa










)(
)...(
...
1
0
1210
1210
0
Deret didefinisikan secara rekursif sebagai berikut:
n
k
ka
0












0,)(
0,
1
0
0
0
naa
na
a
n
n
k
k
n
k
k
Sehingga ,

13. Contoh Fungsi yang di definisikan secara
rekursif (4)
Barisan Fibonacci 0, 1, 1, 2, 3, 5, 8, 11, 19, …. Dapat
dinyatakan secara rekursif sebagai berikut:









 1,
1,1
0,0
21 nff
n
n
f
nn
n

14. Contoh : barisan fibbonaci
f0 = 0, f1 = 1
fn = fn-1+ fn-2, n=2,3,4,…
f0= 0
f1= 1
f2= f1+ f0= 1 + 0 = 1
f3= f2+ f1= 1 + 1 = 2
f4= f3+ f2= 2 + 1 = 3
f5= f4+ f3= 3 + 2 = 5
f6= f5+ f4= 5 + 3 = 8

15. Himpunan yang didefinisikan rekursif
Langkah-langkah dalam mendefinisikan suatu himpunan secara
rekursif:
1. Langkah basis:
Spesifikasi koleksi awal dari anggota
2. Langkah rekursif:
Mendefinisikan aturan konstruksi anggota baru dari anggota yang
telah diketahui

16. Contoh himpunan yang didefinisikan secara
rekursif
Misalkan S didefinisikan secara rekursif oleh:
1) Langkah basis : 3  S
2) Langkah rekursif : Jika x  S dan y  S maka (x+y) 
S
Unsur baru ditemukan di S adalah 3 dengan langkah
basic , 3 + 3 = 6
pada aplikasi pertama dari langkah rekursif :
3 + 6 = 6+3 = 9
Aplikasi kedua dari langkah rekursif :
6 + 6 = 12
dan seterusnya ..

17. Himpunan Rekursif
• String adalah rangkaian sejumlah karakter
Contoh:
‘itb’ disusun oleh karakter i, t,dan b
‘informatika’ disusun oleh karakter i, n, f, o, r, m, a, t, i, k, a
• String kosong (null string) atau ‘’ adalah string dengan panjang nol .
Notasi: 
• Alfabet adalah himpunan karakter yang elemen-elemennya adalah
penyusun string. Notasi: 
Contoh:  = {0, 1},  = {a, b, c, …, z}

18. Himpunan string atas alfabet
Contoh:
• Jika  = {0,1} maka string yang merupakan anggota * adalah:
yang didefinisikan sebagai anggota * dalam,
langkah basis : 0 dan 1 yang dibentuk dalam langkah rekursif pertama.
Langkah rekursif : 00, 01, 10, dan 11 yang dibentuk dalam langkah
rekursif kedua
dst
Definisi 1:
Himpunan string * atas alfabet  dapat didefinisikan secara rekursif oleh:
1. Langkah basis:
  * ( adalah string kosong yang tidak memuat simbol)
2. Langkah rekursif:
Jika w  * dan x   , maka wx  *

19. Himpunan string atas alfabet
Definisi 2 :
Dua string dapat di kombinasi menggunakan operasi
kokatenasi. Ambil  menjadi sebuah simbol himpunan dan *
himpunan string dibentuk dari simbol . Kita dapat
menetapkan rangkaian dua string yang dilambangkan oleh
rekursif sebagai:
1. Langkah basis:
Jika w *, maka w.  = w, dengan  string kosong
2. Langkah rekursif:
Jika w1  * dan w2  * dan x  , maka
w1 . (w2 x) = (w1 . w2) x
w1 . w2 seringkali ditulis sebagai w1 w2

20. Himpunan string atas alfabet
Contoh:
Konkatenasi dari w1 = abra dan
w2 = cadabra adalah:
w1 w2 = abracadabra

21. Himpunan Rooted Trees
• Definisi 3
Himpunan akar pohon, di mana pohon berakar terdiri dari
sebuah himpunan yang mengandung simpul yang disebut
akar, dan ujung-ujungnya yang menghubungkan simpul
tersebut, dapat didefinisikan secara rekursif dengan langkah
:
Langkah basis : simpul r tunggal adalag sebuah akar pohon.
Langkah rekursif : misalkan T1, T2, …, Tn menguraikan pohon
akar dengan akar r1, r2, …, rn. Grafik dibentuk dengan
memulai dengan akar r , yang tidak di salah satu pohon
berakar T1, T2, …, Tn
dan menambahkan keunggulan dari r ke masing-masing
simpul

22. Gambar 3 : Membangun akar pohon

23. Struktur Rekursif
• Struktur data yang penting dalam komputer adalah pohon biner
(binary tree).

25. • Simpul (node) pada pohon biner mempunyai paling banyak dua buah
anak.
• Jumlah anak pada setiap simpul bisa 1, 2, atau 0.
• Simpul yang mempunyai anak disebut simpul cabang (branch node) atau
simpul dalam (internal node)
• Simpul yang tidak mempunyai anak disebut simpul daun (leave).

26. • Pohon biner adalah struktur yang rekursif, sebab setiap simpul
mempunyai cabang yang juga berupa pohon. Setiap cabang disebut
upapohon (subtree).

27. • Oleh karena itu, pohon dapat didefinisikan secara rekursif sebagari
berikut:
(i) Basis: kosong adalah pohon biner
(ii) Rekurens: Jika T1 dan T2 adalah pohon biner, maka 
adalah pohon biner
T1 T2

28. Proses pembentukan pohon biner secara rekursif:
(i) 
(ii)

29. INDUKSI STRUKTURAL
Dalam membuktikan hasil-hasil yang berkaitan dengan himpunan
yang didefinisikan secara rekursif, akan lebih mudah apabila
digunakan suatu bentuk induksi matematika yang disebut induksi
struktural.
Langkah-langkah dalam induksi struktural:
1. Langkah basis:
Menunjukkan bahwa hasil yang akan dibuktikan berlaku untuk
semua anggota awal.
2. Langkah rekursif:
Menunjukkan bahwa jika hasil yang akan dibuktikan berlaku untuk
anggota-anggota yang digunakan untuk membangun anggota baru,
maka hasil tersebut juga berlaku untuk anggota yang baru
dibangun.

30. Contoh himpunan yang didefinisikan secara
rekursif
Misalkan S didefinisikan secara rekursif oleh:
1) Langkah basis : 3  S
2) Langkah rekursif : Jika x  S dan y  S maka (x+y)  S
Maka S adalah himpunan bilangan bulat positif yang habis dibagi 3.
Bukti:
Misalkan A himpunan yang beranggotakan semua bilangan bulat positif
yang habis dibagi 3.
Untuk membuktikan bahwa A = S, harus ditunjukkan
A  S and S  A.
Bagian I: Akan dibuktikan A  S, yaitu menunjukkan bahwa setiap bilangan
bulat positif yang habis dibagi 3 ada di S (dengan menggunakan induksi
matematika).

31. Contoh himpunan yang didefinisikan secara
rekursif
Bagian II: Akan ditunjukkan S  A dengan menggunakan definisi rekursif dari S.
Langkah basis:
Akan ditunjukkan setiap anggota awal S ada di A.
Karena 3 habis dibagi 3 maka 3  A.
Langkah rekursif:
Akan ditunjukkan bahwa setiap bilangan bulat yang dibangun dengan mengunakan
langkah rekursif juga merupakan anggota A, yaitu
(x+y)  A jika x,y  S (yang diasumsikan  A).
Jika x dan y keduanya di A, maka 3 | x dan 3 | y. Akibatnya, 3 | (x + y).
Kesimpulan dari bagian II adalah S  A.
Jadi, secara keseluruhan, berlaku A = S.

32. Contoh himpunan yang didefinisikan secara
rekursif
Misalkan P(n): proposisi “3n anggota S”.
1. Langkah basis: P(1) benar, karena 3  S.
2. Langkah induktif:
Asumsikan P(k) benar, yaitu 3k  S.
Akan ditunjukkan P(k+1) juga benar, yaitu
3(k+1)  S
Karena 3k  Sdan 3  S, berdasarkan definisi rekursif dari S, 3k+3 =
3(k+1) juga ada di S.
3. Konklusi:
Jadi, setiap bilangan bulat positif yang habis dibagi 3 ada di S.
Kesimpulan dari bagian I adalah A  S.

33. Terimakasih