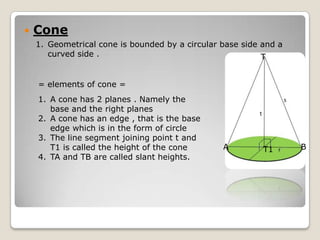
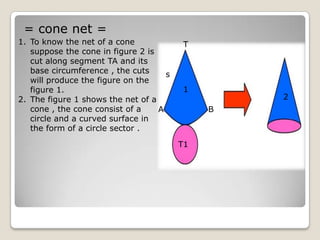
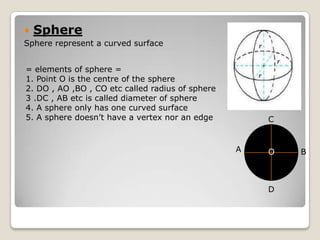
The document describes the geometric formulas for balls and cones. It provides definitions and formulas for calculating the surface area and volume of cones and spheres. For cones, it defines the elements, describes how to make the net, and gives the formulas for surface area and volume. For spheres, it similarly defines the elements, notes they have no net, and provides the formulas for surface area and volume. It also discusses how changing the radius impacts the volume.

1. Describes the geometrical
formulas ball and cone
Members :
1. Andre djisa alhesi samosir
2. Dicky rachmat fauzi
3. Erlangga putra ramadhan
4. Haekal roja
5. Jihan fachry widyatmoko
6. Yogas adi pratama

2.  Cone
1. Geometrical cone is bounded by a circular base side and a
curved side . T
= elements of cone =
1. A cone has 2 planes . Namely the
base and the right planes
2. A cone has an edge , that is the base
edge which is in the form of circle
3. The line segment joining point t and
T1 is called the height of the cone A T1 B
4. TA and TB are called slant heights.

3. = cone net =
1. To know the net of a cone T
suppose the cone in figure 2 is
cut along segment TA and its
base circumference , the cuts s
will produce the figure on the
figure 1. 1
2. The figure 1 shows the net of a 2
cone , the cone consist of a A B
circle and a curved surface in
the form of a circle sector .
T1

4. = surface area of a cone =
We need to know that, the surface of L = surface area
the cone consists of two fields, namely Ba = base area
the curved area (blanket) and a Cs = curved area
circular base field. Sa = surface area
Formula of the surface area of a cone :
L = area of curved surface + circle area
L = ∏ r s + ∏ r2
L=∏r (s+r)
Example :
Known : d : 10 , t : 12 , Cs : 204,1 , Ba : 78,5
Find : Sa
Answer :
L = Cs + Ba => 204,1 + 78,5 = 282,6 cm2

5. = volume of cone =
Formula of volume of cone :
∏ x r x r x h : 3 (∏ x r2 x h x 1/3)
Example :
Known : d : 14 , t : 18 , ∏ : 22/7
Find : volume
Answer :
Volume : ∏ x r2 x h x 1/3 => 22/7 x 7 x7 x 18 x 1/3 = 924

6. =the ratio of cone because of the change=
in radius
Figure 1 illusrates a cone of base radius r1 and
height t . 1
If the base radius r1 is extended twice longer
while the hight is constant , we have a cone in
figure 2 of base radius r2 = 2 r1 and height t
Then :
v1 = 1/3 ∏ r21 t
v2 1/3 ∏ r2 2 t 2
v1 = 1/3 ∏ r21 t  v1 = r21
v2 1/3 ∏ (2r 2 ) t v2 4 r2 1
v1 = 1  v2 = 4 v 1
v2 4

7. Example :
Known : r : 6 , ∏ : 22/7
Find : the volume of the cone if the becomes 2x the original
Answer :
V = 1/3 ∏ r2 t  1/3 x 22/7 x 6 x 6 x 21 792
r1= 2r then v1 = 22 v  4 x 792 = 3.168

8. Cones in daily life

9.  Sphere
Sphere represent a curved surface
= elements of sphere =
1. Point O is the centre of the sphere
2. DO , AO ,BO , CO etc called radius of sphere
3 .DC , AB etc is called diameter of sphere
4. A sphere only has one curved surface
5. A sphere doesn’t have a vertex nor an edge C
A O B
D

10. = sphere net =
We can’t make a net from a sphere

11. = the surface area of a sphere =
Sa of a sphere= 2 x the area hemisphere  2 x ( 2 x ∏ r2 ) =
4∏r2
example :
Known : r : 10,5 , ∏ : 22/7
Find : Sa
Answer :
L = 4∏r2  4 x 22/7 x 10,5 x 10,5 = 1,386

12. = volume of sphere =
v = 4 x the cone volume  4 x 1/3 ∏ r2 t  4/3 ∏ r2 t
Since the height of the cone = the ball radius , or t = r
The ball volume : 4/3 ∏ r2 t = 4/3 ∏ r3
Example :
Known : d : 12 , ∏ : 3,14
Answer :
V : 4/3 x ∏ x r3  4/3 x 3,14 x 6 x 6 x 6 = 904,32 cm cm3

13. the ratio of the sphere volume because of
the change in radius
If the radius of a sphere is extented n times the original , then
the
volume of the sphere enlarges n3 times the original volume , in
other words v1 : v1 = 1 : n3
Example :
Known : v : 113,04 cm3
find : 3/2 times the original length
Answer :
r1 = 3/2 r => v1 = (3/2)3 v = 27/8 x 113,04 = 381,51

14. Thank you for your attention
Success comes to those who would still try though never do
wrong. Those who never give up, because the spirit is still
there.