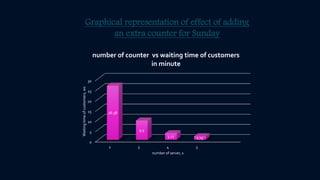
This document discusses applying queuing theory to improve service efficiency at a bank. It analyzes customer arrival and service rates to model the bank's queues. The model, M/M/C, is used to calculate key metrics like expected wait times. Adding an extra server on busy days can significantly reduce wait times, as can improving the service rate. Properly applying queuing theory through data analysis and modeling can help banks optimize their service levels and increase customer satisfaction.

1. QUEUEING MODEL OF
AXIS BANK
SUBMITTED BY:-
PRAVIN KUMAR

2. What is the Queuing Theory?
• Queue - a line of people or vehicles waiting for something.
• Queuing Theory- Mathematical study of waiting lines, using models to
show results, and show opportunities within arrival, service, and
departure processes.
• In this paper, queue theory is applied to enhance the service of a bank in
lines. For this, firstly a queue model (M/M/C): (GD/∞/∞) is selected to
find out efficiency of the servers.

3. Objectives of the project
• Finding out the efficiency of the servers.
• Signifying the number of service facilities.
• The amount of time customers has to spend to get the desired service.
• The length of the queue (Waiting line).
• How much time the customers have to wait before the service starts.
• the optimal number of counter is calculated to improve the operational
efficiency.

4. Significance of Queuing models
• Queuing Models Calculate the best number of servers to minimize
costs.
• Queue lengths and waiting times can be predicted.
• Improve Customer Service, continuously.
• When a system gets congested, the service delay in the system
increases.
• A good understanding of the relationship between congestion and delay
is essential for designing effective congestion control for queuing
system.
• Queuing Theory provides all the tools needed for this analysis.

5. Literature Review
Salzarulo Peter, June 2016: He suggested when scheduling appointments,
health care facilities must estimate patient examination durations. It is apparent
that as these estimates become more accurate, more precise schedules can be
developed and this may result in improvements to service provider idle time,
patient wait time, and facility overtime.
http://onlinelibrary.wiley.com/doi/10.1111/poms.12528/epdf?r3_referer=wol&tracking_action=preview_click&
show_checkout=1&purchase_referrer=onlinelibrary.wiley.com&purchase_site_license=LICENSE_DENIED
Schultz Kenneth ,November-December 2011: He suggested patient service
measures are affected by system variability, as are health car e costs due to
variability’s effect on the availability of key resources such as equipment and
personnel.
http://onlinelibrary.wiley.com/doi/10.1111/j.1937-
5956.2010.01210.x/epdf?r3_referer=wol&tracking_action=preview_click&show_checkout=1&purchase_referr
er=onlinelibrary.wiley.com&purchase_site_license=LICENSE_DENIED

6. Terminology and Notations
• M=Number of servers
• Pn= probability of exactly “n” customers in the system.
• N= number of customers in the system.
• Ls= expected number of customers in the system
• Lq= expected number of customers in the queue.
• Ws= waiting time of customers in the system
• Wq= waiting time of customers in the queue.
• λn= The mean arrival rate of new customers are in systems.
• µn= The mean service rate for overall systems when “n” customers are in systems.
• The mean arrival rate is constant for all n, this is denoted by λ and the mean service rate per busy server is constant for all
n≥1, is denoted by µ. And when n ≥M that is all z servers are busy, µ=sµ. Under this condition,
• The expected inter-arrival time is 1/λ
• The expected service time is 1/µ.
• The utilization factor for the service facility is ρ= λ/Mµ.

7. Formula 1 [Adding another server to the system during
busy days (Increase server)]
PROPOSED MODEL: (M/M/C): (GD/∞/∞) model:
• The probability of no customer in the bank,
P0=
1
𝑛=0
𝑠−1
𝜆
𝜇
𝑛
𝑛!
+
𝜆
𝜇
𝑠
𝑠!
∗
1
1−
𝜆
𝑠𝜇
• The probability of n customers in the bank,
𝝀
𝝁
𝒏!
𝒑0 if 0≤ 𝒏 ≤ 𝒔
Pn=
𝝀
𝝁
𝒔!𝒔 𝒏−𝒔 𝒑0 if n≥ 𝒔

8. Expected number of customers in the bank,
Ls=Lq+ (
𝜸
𝝁
)
Expected number of customers in the bank line,
Lq=p0
𝝀
𝝁
𝒔
𝝆
𝒔!(𝟏−𝝆) 𝟐
Expected number of waiting time in line,
Wq=Lq/𝝀
Expected waiting time in bank (In line + in server),
W=Wq+
𝟏
𝝁
Service factor,
ρ=
𝝀
𝝁

9. Case study of a local bank
[Service time per day is 10:00 to 1:00 and 3:00-4:00.total 240
minutes.]
Bank data of customer count for one
month
Week No. Monday Tuesday Wednesday Thursday Friday
Week 1 140 114 132 146 156
Week 2 120 123 199 145 150
Week 3 199 171 159 120 130
Week 4 150 180 149 107 110
Total 609 588 639 518 546
Average 152.25 147 159.75 129.5 136.5

10. 0
5
10
15
20
25
30
2 3 4 5
26.58
9.5
3.27 1.75
Waitingtimeofcustomers,ws
number of server, s
number of counter vs waiting time of customers
in minute
Graphical representation of effect of adding
an extra counter for Sunday

11. Problem Formulation
• It has been seen in the research that If waiting time increases then
frustration level increases with this. In the scenario utilization factor
is as high as 0.39 to 0.48 during busy days of the bank. It is clear that
high utilization rate is not helping to reduce customer’s waiting time in
queue. On high utilization factor customers have to wait more time in
system as like as 26.58, 15.123, 96.664, 4.992, 7.074 minutes
respectively from Monday to Friday. It seems that there is a problem
in the operations which if not noticed could reduce business of bank.

12. Result and discussion of formula 1
• The comparative analysis of adding an extra counter to the system and
improving the service rate have shown in the above figures.
• when one more counter is added (s=3) the waiting time in system
reduces significantly to 9.5, 5.624, 33.923, 2.387, 3.025 minutes
respectively from Monday to Thursday. However, it can be seen that
adding one more counter (s=3) does significantly change the waiting
time of the system except for Tuesday. Using four counter for Tuesday
significantly changes waiting time from 33.923 (when s=3) to 9.217.

13. • The second way of reducing the waiting time in line is by improving the
service rate. The above figure indicates the ultimate effect of improving
the service rate. From the comparative analysis, it can be seen that on
Tuesday, if the service rate is improved from .70 to .76 then waiting
time reduces to 96.664 to 14.12 (82.554minutes) without adding an
extra counter thus adding no extra cost.
Result and discussion of formula 2

14. Psychological View [Frustration]

15. Conclusion
The efficiency of commercial banks is improved by the following three
measures:
• The queuing number
• The service stations number and
• The optimal service rate
which are investigated by means of queuing theory. By the example, the
results are effective and practical. The time of customer queuing is
reduced. The customer satisfaction is increased. It was proved that this
optimal model of the queuing is feasible.

16. Bibliography
• http://people.brunel.ac.uk/~mastjjb/jeb/or/queue.html
• http://www.supositorio.com/rcalc/rcalclite.htm
• http://www.shmula.com/queueing-theory-part-3/170/
• http://www.ams.sunysb.edu/~jsbm/courses/342/examples-queueing