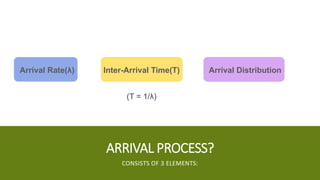
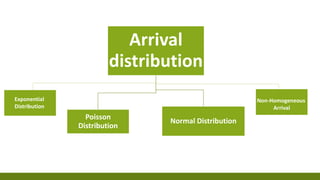
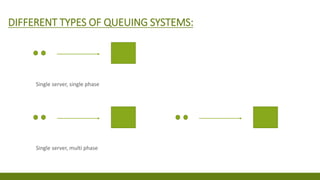
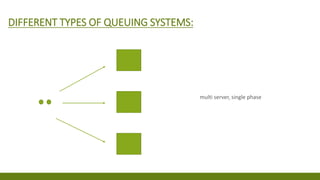
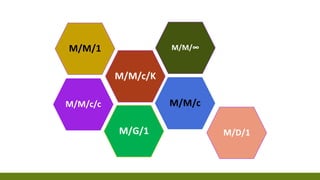
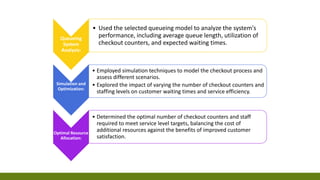
The document provides an overview of queuing theory, outlining its principles, models, and applications in optimizing service systems such as retail and healthcare. It discusses various types of queue disciplines, the mathematical framework using Kendall notation, and presents case studies demonstrating the practical application of these theories to improve customer service and efficiency. Additionally, it includes specific problems and solutions illustrating calculations related to queue performance metrics.