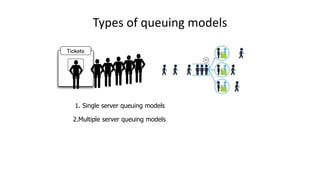
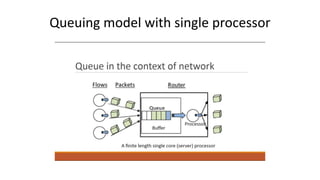
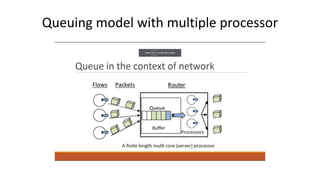
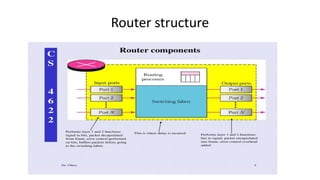
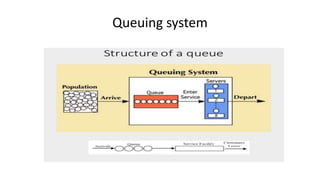
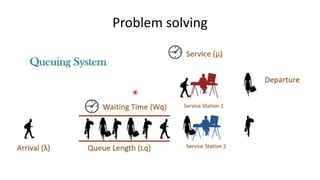
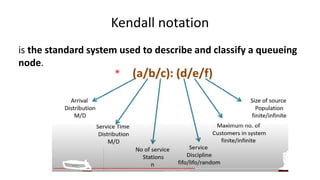
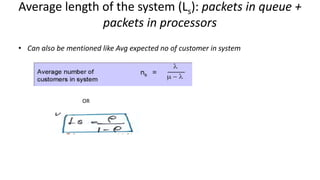
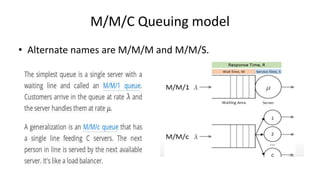
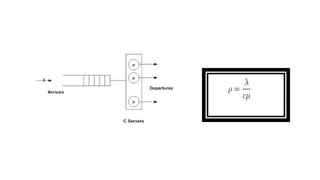
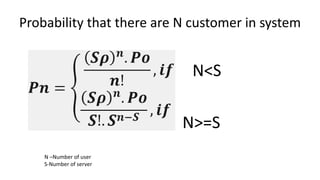
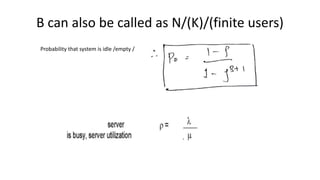
Queuing theory is a mathematical study of waiting lines, analyzing components like arrival and service processes, servers, and customer populations. It categorizes queuing models into types such as single and multiple server models, and finite as well as infinite queues, while addressing queuing discipline, utilization, and performance metrics. The document also presents various problems and simulations related to queuing scenarios across different service systems.

1. Queuing theory

2. Queuing theory
• Queuing theory is a branch of mathematics that studies how
lines form, how they function, and why they malfunction
• Queuing theory examines every component of waiting in line, including the
arrival process, service process, number of servers, number of system places,
and the number of customers—which might be people, data packets, cars, or
anything else.

3. Queuing theory
• Queuing models are also called waiting line models.
• Queuing theory is the mathematical study of queuing, or waiting lines.
• A basic queuing system consists of an arrival process (how customers arrive
at the queue), the queue itself, the service process for attending to those
customers, and departures from the system

4. Types of queuing models
1. Single server queuing models
2.Multiple server queuing models

5. Finite and infinite queues(populations )
• The infinite queue length model assumes, that every person who comes will joins the
line, for example, if already three people are waiting for the doctor, the fourth
person will join the line and so on. There is no restriction on the number of people
who are actually waiting or there is no restriction on the length of the queue. The
queue length can theoretically be infinite so it can go on and on.
• In finite queue length models we try to restrict the queue length to
a certain limit after which we say that if this threshold limit is
reached, people who come into the system do not join the system

6. Queuing model with single processor

7. Queuing model with multiple processor

9. Router structure

10. Queuing system

11. Types of Buffering :
• Zero Capacity –
This queue cannot keep any message waiting in it. Thus it has maximum
length 0. For this, a sending process must be blocked until the receiving
process receives the message. It is also known as no buffering.
• Bounded Capacity –
This queue has finite length n. Thus it can have n messages waiting in it. If
the queue is not full, new message can be placed in the queue, and a
sending process is not blocked. It is also known as automatic buffering.
• Unbounded Capacity –
This queue has infinite length. Thus any number of messages can wait in it.
In such a system, a sending process is never blocked.

12. Queuing discipline
1. FIFO (First In First Out) or FCFS (First Come First Serve)
2. LIFO (Last In First Out)
3. SIRO (Service In Random Order)
4. Priority Queue

13. Problem solving

14. • Arrival rate
– It represents the number of jobs/packets arriving into a system in unit time
– Can follow any distribution, but most of the times arrival rate follows Poisson distribution
• It is represented by lambda (λ)
• Service rate
– It represents the number of jobs/packets served in unit time
– Service rate follows exponential distribution
• It is represented by mu (μ)

15. Kendall notation
is the standard system used to describe and classify a queueing
node.

17. Kendall notation(with different notations and
meaning)

18. Consider a queue with one server and the following
characteristics
• λ: the arrival rate (the reciprocal of the expected time between each
customer arriving, e.g. 10 customers per second);
• μ: the reciprocal of the mean service time (the expected number of
consecutive service completions per the same unit time, e.g. per 30
seconds);
• n: the parameter characterizing the number of customers in the system;
• Pn: the probability of there being n customers in the system in steady state.

19. parameters
• Average length of the queue (Lq)
• Average length of the system (Ls): packets in queue + packets in
processors
• Average waiting time in the queue (Wq)
• Average waiting time in the system (Ws): waiting time in queue +
processing time

20. SCOPE

21. Formulas to be remembered
• Traffic intensity (utilization factor) /server utilization

22. Average length of the system (Ls): packets in queue +
packets in processors
• Can also be mentioned like Avg expected no of customer in system
OR

23. Average length of the queue (Lq)
• Can also be mentioned like Avg expected no of customer in
QUEUE
OR
OR

24. Average waiting time in the system (Ws): waiting
time in queue + processing time
OR

25. Average waiting time in the queue (Wq)
OR

26. Probability that no customer in system(system
empty/system idle)
OR

27. Probability that n customer in system

28. Problem 1
• Students arrive at the head office of Universal Teacher
Publications according to a Poisson input process with a mean
rate of 40 per hour. The time required to serve a student has
an exponential distribution with a mean of 50 per hour.
Assume that the students are served by a single individual, find
the average waiting time of a student.

29. Problem 2
A Television repairman finds that the time spent on his jobs has
an exponential distribution with mean 30 minutes. If he repairs
the sets in the order in which they come in, and if the arrivals of
sets are approximately Poisson with an average rate of 10 per 8
hours per day , what is the repairs man idle time each day ?Find
the expected number of units in the system and in the
queue?(How many jobs are ahead of
the average set just brought in?)

30. Problem 3
A self service store employs one cashier at its counter. Nine
customers arrive on an average every 5 minutes. While the
cashier can serve 10 customers in 5 minutes. Assuming poisson
distribution for the arrival rate and exponential distribution for
service time. Find(a) Average number of customers in the
system.(b) Average number of customers in the queue or average
queue length.(c) Average time, a customer spends in the
system.(d) Average time, a customer waits before being served.

31. Problem :4
• Arrivals to a router with single core processor are Poisson
distributed with a rate of 20 per minute. The average time for a
packet to get service is 2 seconds and this time is exponentially
distributed. What would be the average waiting time of a
packet in the system, average length of packets in the queue,
and average response time?(response time =ws)

32. Problem :5
• An airline organization has one reservation clerk on duty in its local
branch at any given time. The clerk handles information regarding
passenger’s reservation and flight timings. Assume that the number
of customers arriving during any given period in Poisson
distribution with an arrival rate of 8 per hour and that the
reservation clerk can serve a customer in 6 minutes on an average,
with an exponentially distributed time. (i) What is the probability
that the system is busy. (ii) What is the average time a customer
spends in the system. (iii) What is the average length of the queue
and what is the number of customers in the system

33. Problem :6
• On an average 96 patients per 24-hours day require the service of an
emergency clinic. Also on the average a patient requires 10 minute of
active attention.
• Assume that the facility can handle only one emergency at a time suppose
that it costs the clinic Rs.100 per patient treated to obtain an average
servicing time of 10 minute, and that each minute of decrease in this
average time would cost the clinic Rs.10 per patient treated.
• How much would have to be budgeted by the clinic to decrease the
average size of the queue from 4/3 to 1/2

38. M/M/C Queuing model
• Alternate names are M/M/M and M/M/S.

40. M/M/M Queuing model FORMULAS

41. Probability that there are N customer in system
N<S
N>=S
N –Number of user
S-Number of server

42. Probability that user must wait in queue(N>S)
• N –Number of user
• S-Number of server
•Pr=

43. Expected length of queue=Lq

44. • Ls=
• Ws=
•
Wq=

45. Problem:1
A supermarket has two girls ringing up sales at the counters. If the
service time for each customer is exponential with mean 4 mins, and
people arrive in a Poisson fashion at the counter at the rate of10 an
hour.
a) What is the expected percentage of idle time for each girl?
b) The expected waiting time for a customer in the system.
c) What is the probability that user must wait for service.

46. Problem:2
• There are two typists in an office. Each typist can type an
average of 6 letters per hour. If letters arrive for being typed at
the rate of 15 letters per hour, Assume that arrival and service
rates follow poisson distribution.
• (a) What fraction of the time all the typists will be busy?
• (b) What is the average number of letters waiting to be typed?

47. M/M/1/K Model(Finite Capacity Queueing Model)
• Can also be represented as M/M/1/N/FCFS Model
• The capacity of the system is finite and is K.
• The customers are served in order of their arrival, i.e. the
queue discipline is First-Come, First-Served (FCFS).
• There is only one server in the system. The service times are
independently, identically and exponentially distributed with
parameter .

48. B can also be called as N/(K)/(finite users)
Probability that system is idle /empty /

49. Probability that there are N Customer

50. Lq=
Ws=

51. Effective arrival rate
When there are B users in the system, a new incoming user may not
be taken into the queue (new packets could be dropped). Therefore, the
effective arrival λ eff is given by,
λ ef f = λ(1 − PN) = λ(1 − ρBp0)

52. Problem 1

53. Problem 2
Patients arrive at a clinic according to Poisson distribution at the rate of
30 patients per hour. The waiting room does not accommodate more
than 14 patients. Examination time per patient is exponential with a
mean rate of 20 per hour.
(1) Find the effective arrival rate at the clinic
(2) What is the probability that an arriving patient will not wait?
(3) What is the expected waiting time until a patient is discharged from
the clinic?

54. • https://www.youtube.com/watch?v=SqSUJ0UYWMQ(basic)
• https://pt.slideshare.net/YogeshKumbhar1
• https://www.youtube.com/watch?v=4iYDVsk_64E
• https://www.youtube.com/watch?v=OPNFPMrFxVc
• https://www.youtube.com/watch?v=UuvnIYIL8jo
• https://www.youtube.com/watch?v=78Z-4_o8sIE&t=877s
• https://www.youtube.com/watch?v=qWiBZOT-MgQ

55. M/M/1
• https://www.youtube.com/watch?v=SqSUJ0UYWMQ(basic)
• https://pt.slideshare.net/YogeshKumbhar1
• https://www.youtube.com/watch?v=4iYDVsk_64E
• M/M/C queuing model
• https://www.youtube.com/watch?v=UuvnIYIL8jo
• https://www.youtube.com/watch?v=78Z-4_o8sIE
• https://slideplayer.com/slide/3891477/
• m/m/1/k
• https://www.youtube.com/watch?v=rEM_SSqb2yU
• https://www.youtube.com/watch?v=25-K5S9ons0&t=681s