The document discusses querying temporal databases using an interval-based query language combining conjunctive queries with temporal logic in the context of ontology-based data access. This approach aims to enhance the capabilities of querying relational databases by enabling access to temporal data similar to how OWL 2 QL operates on static data. The authors propose techniques for rewriting temporal queries into SQL while addressing key challenges such as temporal joins and coalescing overlapping intervals.

1. Querying Temporal Databases via OWL 2 QL
Szymon Klarman and Thomas Meyer
Centre for Artificial Intelligence Research,
CSIR Meraka Institute & University of KwaZulu-Natal,
South Africa
September 16, 2014
RR-14, Athens

2. RR 2014 Querying Temporal Databases via OWL 2 QL
Problem and motivation
Ontology-based data access is a paradigm of querying relational data via
ontological (semantic) layer (OWL 2 QL ∼ DL-Lite):
data + conjunctive query + ontology SQL query + RDBMS.
Problem:
Can we use a similar approach to accessing temporal databases?
(SQL:2011 in IBM DB2 10.1, Oracle DB 11g Workspace Manager, etc.)
Approach:
We propose an interval-based temporal query language which:
• modularly combines CQs with temporal logic (FOMLO),
• enables reuse of rewriting techniques for CQs (in OWL 2 QL),
• is easily rewritable into SQL (AC0 data complexity).
S. Klarman and T. Meyer 1 / 16

3. RR 2014 Querying Temporal Databases via OWL 2 QL
DL-Lites
A family of Description Logics used for ontology-based data access:
• ABox A (data): Employee(john), worksAt(john, dep1)
• TBox T (ontology): Employee Person, worksAt isEmplyedAt
• conjunctive query: ∃y.ϕ(x, y), where ϕ is a conjunction of atoms:
q(x) := ∃z.(Person(x) ∧ worksAt(x, z) ∧ basedIn(z, barcelona))
• CQ answering via FO rewriting, using existing RDBMSs:
T , A |= q iff db(A) |= qT
where db(A) is A viewed as a database (unique minimal model).
S. Klarman and T. Meyer 2 / 16

4. RR 2014 Querying Temporal Databases via OWL 2 QL
Ontology-based access to temporal DBs
Temporal database:
Emp
id name department from to
e1 john d1 1998 2000
e1 john d3 2000 2003
e2 mark d2 1999 2002
Dep
id type location from to
d1 financial madrid 1998 1999
d1 financial barcelona 1999 2003
d2 hr barcelona 2000 2003
d3 hq london 2000 2003
S. Klarman and T. Meyer 3 / 16

5. RR 2014 Querying Temporal Databases via OWL 2 QL
Ontology-based access to temporal DBs
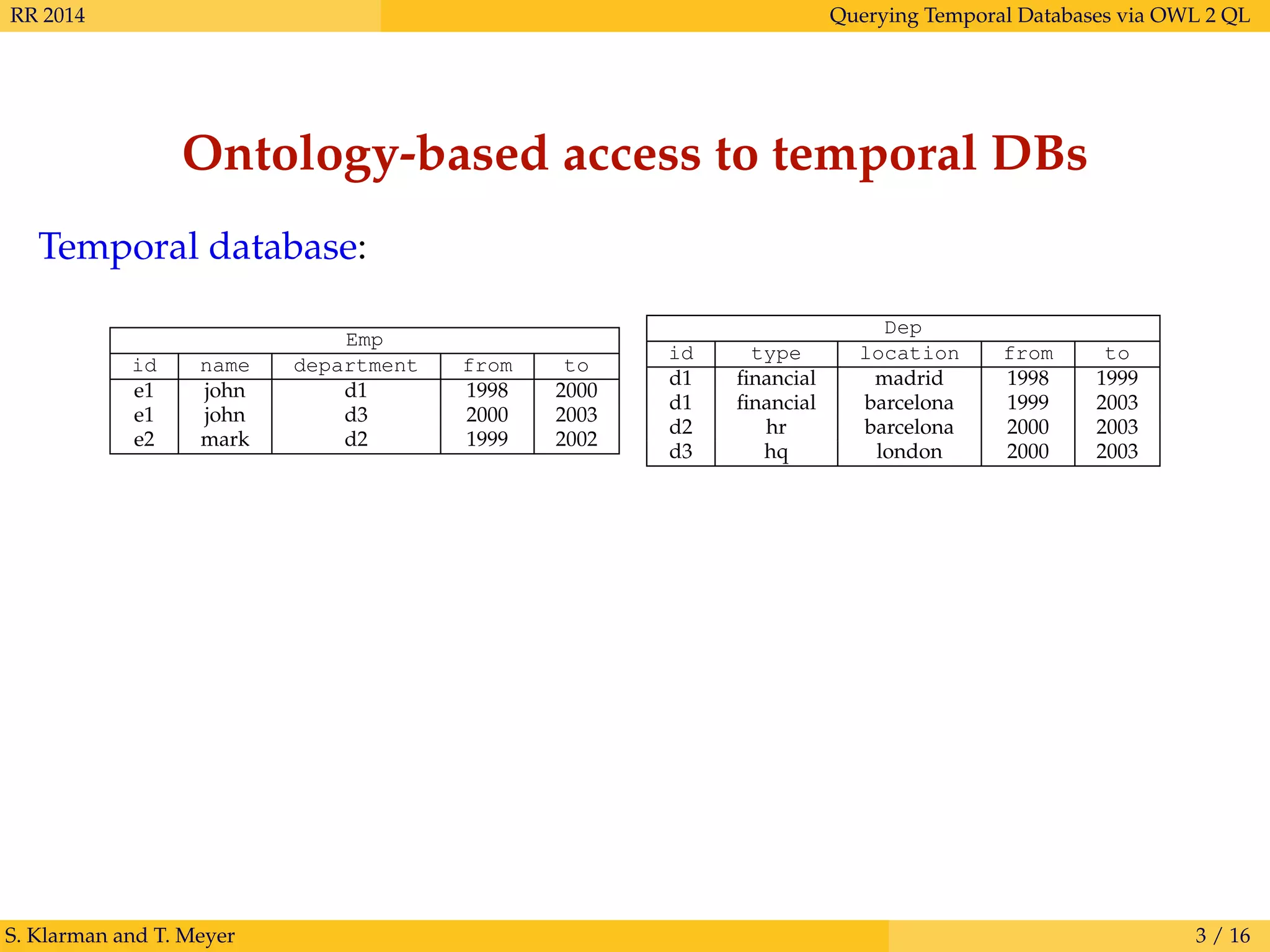
Temporal database:
Emp
id name department from to
e1 john d1 1998 2000
e1 john d3 2000 2003
e2 mark d2 1999 2002
Dep
id type location from to
d1 financial madrid 1998 1999
d1 financial barcelona 1999 2003
d2 hr barcelona 2000 2003
d3 hq london 2000 2003
(Virtual) temporal ABox:
[1998, 2000] : Emp(e1)
[1998, 2000] : name(e1, john)
[1998, 2000] : department(e1, d1)
. . .
[1998, 1999] : Dep(d1)
[1998, 1999] : type(d1, financial)
[1998, 1999] : location(d1, madrid)
. . .
S. Klarman and T. Meyer 3 / 16

6. RR 2014 Querying Temporal Databases via OWL 2 QL
Ontology-based access to temporal DBs
Temporal database:
Emp
id name department from to
e1 john d1 1998 2000
e1 john d3 2000 2003
e2 mark d2 1999 2002
Dep
id type location from to
d1 financial madrid 1998 1999
d1 financial barcelona 1999 2003
d2 hr barcelona 2000 2003
d3 hq london 2000 2003
(Virtual) temporal ABox:
[1998, 2000] : Emp(e1)
[1998, 2000] : name(e1, john)
[1998, 2000] : department(e1, d1)
. . .
[1998, 1999] : Dep(d1)
[1998, 1999] : type(d1, financial)
[1998, 1999] : location(d1, madrid)
. . .
TBox: {Emp Person, department worksAt, location basedIn}
S. Klarman and T. Meyer 3 / 16

7. RR 2014 Querying Temporal Databases via OWL 2 QL
Ontology-based access to temporal DBs
Temporal database:
Emp
id name department from to
e1 john d1 1998 2000
e1 john d3 2000 2003
e2 mark d2 1999 2002
Dep
id type location from to
d1 financial madrid 1998 1999
d1 financial barcelona 1999 2003
d2 hr barcelona 2000 2003
d3 hq london 2000 2003
Query:
Find all persons X and times Y, such that X worked at a department based in
Barcelona during Y and in a department based in Madrid some time earlier.
Answers, e.g.:
X = e1 as Y = [1999, 2000].
S. Klarman and T. Meyer 3 / 16

8. RR 2014 Querying Temporal Databases via OWL 2 QL
Temporal data
Time:
A time domain is a pair (T, <) (linear, point-based). An interval
τ = [τ−, τ+], for τ− ≤ τ+ ∈ T, is the set {t ∈ T | τ− ≤ t ≤ τ+}.
Temporal ABoxes:
A concrete temporal ABox is a set A of time-stamped ABox axioms:
τ : α
where τ is an interval and α is an ABox axiom, e.g.:
[1, 2] : Employee(john), [2, 2] : worksAt(john, dep1)
Every A corresponds to some abstract temporal ABox via a mapping
· , such that A = (At)t∈T, where
At = {α | τ : α ∈ A and t ∈ τ}.
S. Klarman and T. Meyer 4 / 16

9. RR 2014 Querying Temporal Databases via OWL 2 QL
Temporal query language: syntax
• an interval-based temporal language (FOMLO),
• epistemic interpretation of CQs in the temporal language.
TQL formulas:
ψ ::= [q](u) | u∗ < v∗ | ¬ψ | ψ1 ∧ ψ2 | ∃y.ψ
where:
• q is a CQ,
• u, v, y are temporal interval terms,
• ∗ ∈ {−, +}.
Example:
ψ(x, y) := [∃z.(Person(x) ∧ worksAt(x, z) ∧ basedIn(z, barcelona))](y) ∧
∃v.(v+
< y−
∧ [∃z.(worksAt(x, z) ∧ basedIn(z, madrid))](v))
S. Klarman and T. Meyer 5 / 16

10. RR 2014 Querying Temporal Databases via OWL 2 QL
Temporal query language: semantics
For a (temporal) substitution π:
T , A, π |= u∗
< v∗
iff π(u)∗
< π(v)∗
,
T , A, π |= ¬ψ iff T , A, π |= ψ,
T , A, π |= ψ1 ∧ ψ2 iff T , A, π |= ψ1 and T , A, π |= ψ2,
T , A, π |= ∃y.ψ iff there exists τ ∈ I, such that
T , A, π[y → τ] |= ψ.
CQs are embedded in TQL using epistemic semantics.
T , A, π |= [q](u) iff T , At |= q, for every t ∈ π(u)
Therefore...
• read [q](τ) as: it is true that q is entailed in all time points in τ.
• ¬[q](τ) interpreted via negation-as-failure: it is not true that...
• CQ rewriting can be directly applied:
T , At |= q iff tdb(At) |= qT
S. Klarman and T. Meyer 6 / 16

11. RR 2014 Querying Temporal Databases via OWL 2 QL
From DLs to 2FO
Two-sorted FO language:
ϕ ::= R(d1, . . . , dn, t1, t2) | ¬ϕ | ϕ1 ∧ ϕ2 | t1 < t2 | ∃x.ϕ | ∃y.ϕ
Temporal database:
The temporal database corresponding to A is the tuple
tdb(A) = (NI, T, <, ·D), where:
• NI is the data domain and (T, <) the time domain,
• ·D is the interpretation over Γ = {Rα | α ∈ NC ∪ NR}, where:
• RD
A = {(a, τ−
, τ+
) | τ : A(a) ∈ A}, for every A ∈ NC,
• RD
r = {(a, b, τ−
, τ+
) | τ : r(a, b) ∈ A}, for every r ∈ NR.
S. Klarman and T. Meyer 7 / 16

12. RR 2014 Querying Temporal Databases via OWL 2 QL
Query answering
Temporal semantics is not effectively supported by SQL:2011 systems:
tdb(A) RA(a, t1, t2) iff (a, t1, t2) ∈ RD
A
E.g., for A = {[1, 2] : A(a), [2, 3] : A(a)} we get:
tdb(A) RA(a, 1, 3)
Key problems:
• computing temporal joins, i.e., identifying maximal time intervals
over which conjunctions of atoms are satisfied,
• applying coalescing, i.e., merging overlapping and adjacent
intervals for the (intermediate) query results.
S. Klarman and T. Meyer 8 / 16

13. RR 2014 Querying Temporal Databases via OWL 2 QL
Query answering
temp. ABox: {[1, 7] : B(a), [1, 3] : C(a), [3, 10] : C(a), [6, 12] : D(a)}
TBox: {D B}
TQL query: [q(a)]([2, 9]), where q(x) = B(x) ∧ C(x)
S. Klarman and T. Meyer 9 / 16

14. RR 2014 Querying Temporal Databases via OWL 2 QL
Query answering
temp. ABox: {[1, 7] : B(a), [1, 3] : C(a), [3, 10] : C(a), [6, 12] : D(a)}
TBox: {D B}
TQL query: [q(a)]([2, 9]), where q(x) = B(x) ∧ C(x)
S. Klarman and T. Meyer 9 / 16
RB(a, 1, 7)
RD(a, 6, 12)
RC(a, 3, 10)
RC(a, 1, 3)
1 2 3 4 5 6 7 8 9 10 11 12

15. RR 2014 Querying Temporal Databases via OWL 2 QL
Query answering
temp. ABox: {[1, 7] : B(a), [1, 3] : C(a), [3, 10] : C(a), [6, 12] : D(a)}
TBox: {D B}
TQL query: [q(a)]([2, 9]), where q(x) = B(x) ∧ C(x)
S. Klarman and T. Meyer 9 / 16
RB(a, 1, 7)
RD(a, 6, 12)
RC(a, 3, 10)
RC(a, 1, 3)
1 2 3 4 5 6 7 8 9 10 11 12
q2(x) = D(x) ∧ C(x)
q1(x) = B(x) ∧ C(x)

16. RR 2014 Querying Temporal Databases via OWL 2 QL
Query answering
temp. ABox: {[1, 7] : B(a), [1, 3] : C(a), [3, 10] : C(a), [6, 12] : D(a)}
TBox: {D B}
TQL query: [q(a)]([2, 9]), where q(x) = B(x) ∧ C(x)
S. Klarman and T. Meyer 9 / 16
RB(a, 1, 7)
RD(a, 6, 12)
RC(a, 3, 10)
Rq1
(a, 3, 7)
Rq2
(a, 6, 10)
RC(a, 1, 3)
Rq1
(a, 1, 3)
Rqi
1 2 3 4 5 6 7 8 9 10 11 12
q2(x) = D(x) ∧ C(x)
q1(x) = B(x) ∧ C(x)

17. RR 2014 Querying Temporal Databases via OWL 2 QL
Query answering
temp. ABox: {[1, 7] : B(a), [1, 3] : C(a), [3, 10] : C(a), [6, 12] : D(a)}
TBox: {D B}
TQL query: [q(a)]([2, 9]), where q(x) = B(x) ∧ C(x)
S. Klarman and T. Meyer 9 / 16
RB(a, 1, 7)
RD(a, 6, 12)
RC(a, 3, 10)
Rq1
(a, 3, 7)
Rq2
(a, 6, 10)
RC(a, 1, 3)
Rq1
(a, 1, 3)
Rqi
1 2 3 4 5 6 7 8 9 10 11 12 qT
(x) = q1(x) ∨ q2(x)
q2(x) = D(x) ∧ C(x)
q1(x) = B(x) ∧ C(x)

18. RR 2014 Querying Temporal Databases via OWL 2 QL
Query answering
temp. ABox: {[1, 7] : B(a), [1, 3] : C(a), [3, 10] : C(a), [6, 12] : D(a)}
TBox: {D B}
TQL query: [q(a)]([2, 9]), where q(x) = B(x) ∧ C(x)
S. Klarman and T. Meyer 9 / 16
RB(a, 1, 7)
RD(a, 6, 12)
RC(a, 3, 10)
Rq1
(a, 3, 7)
Rq2
(a, 6, 10)
RC(a, 1, 3)
Rq1
(a, 1, 3)
RqT (a, 1, 3)
RqT (a, 3, 7)
RqT (a, 6, 10)
Rqi
RqT
1 2 3 4 5 6 7 8 9 10 11 12 qT
(x) = q1(x) ∨ q2(x)
q2(x) = D(x) ∧ C(x)
q1(x) = B(x) ∧ C(x)

19. RR 2014 Querying Temporal Databases via OWL 2 QL
Query answering
temp. ABox: {[1, 7] : B(a), [1, 3] : C(a), [3, 10] : C(a), [6, 12] : D(a)}
TBox: {D B}
TQL query: [q(a)]([2, 9]), where q(x) = B(x) ∧ C(x)
S. Klarman and T. Meyer 9 / 16
RB(a, 1, 7)
RD(a, 6, 12)
RC(a, 3, 10)
Rq1
(a, 3, 7)
Rq2
(a, 6, 10)
RqT (a, 1, 10)coal
RC(a, 1, 3)
Rq1
(a, 1, 3)
RqT (a, 1, 3)
RqT (a, 3, 7)
RqT (a, 6, 10)
Rqi
RqT
RqT
coal
1 2 3 4 5 6 7 8 9 10 11 12 qT
(x) = q1(x) ∨ q2(x)
q2(x) = D(x) ∧ C(x)
q1(x) = B(x) ∧ C(x)

20. RR 2014 Querying Temporal Databases via OWL 2 QL
Query answering
temp. ABox: {[1, 7] : B(a), [1, 3] : C(a), [3, 10] : C(a), [6, 12] : D(a)}
TBox: {D B}
TQL query: [q(a)]([2, 9]), where q(x) = B(x) ∧ C(x)
S. Klarman and T. Meyer 9 / 16
RB(a, 1, 7)
RD(a, 6, 12)
RC(a, 3, 10)
Rq1
(a, 3, 7)
Rq2
(a, 6, 10)
RqT (a, 1, 10)coal
RC(a, 1, 3)
Rq1
(a, 1, 3)
RqT (a, 1, 3)
RqT (a, 3, 7)
RqT (a, 6, 10)
Rqi
RqT
RqT
coal
1 2 3 4 5 6 7 8 9 10 11 12
coal
[q(a)]([2,9])
qT
(x) = q1(x) ∨ q2(x)
q2(x) = D(x) ∧ C(x)
q1(x) = B(x) ∧ C(x)

21. RR 2014 Querying Temporal Databases via OWL 2 QL
Query rewriting
For [q(a)]([2, 9]), where q1(a) = B(a) ∧ C(a) and q2(a) = D(a) ∧ C(a):
[q(a)]([2, 9]) 2FO
∃t1, t2.(Rcoal
qT (a, t1, t2) ∧ t1 ≤ 2 ∧ 9 ≤ t2)
Rcoal
qT (a, t1, t2) ∃t3, t4.RqT (a, t1, t3) ∧ RqT (a, t4, t2) ∧
¬∃t5, t6.(RqT (a, t5, t6) ∧ t5 < t1 ∧ t1 ≤ t6) ∧
¬∃t5, t6.(RqT (a, t5, t6) ∧ t5 ≤ t2 ∧ t2 < t6) ∧
¬∃t5, t6.(RqT (a, t5, t6) ∧ t1 < t5 ∧ t6 ≤ t2 ∧
¬∃t7, t8.(RqT (a, t7, t8) ∧ t7 < t5 ∧ t5 ≤ t8))
RqT (a, u, v) Rq1
(a, u, v) ∨ Rq2
(a, u, v)
Rq1
(a, u, v) ∃t1, . . . , t4.(RB(a, t1, t2) ∧ RC(a, t3, t4)) ∧
u = max(t1, t3) ∧ v = min(t2, t4) ∧ u ≤ v
Rq2
(a, u, v) ∃t1, . . . , t4.(RD(a, t1, t2) ∧ RC(a, t3, t4)) ∧
u = max(t1, t3) ∧ v = min(t2, t4) ∧ u ≤ v
S. Klarman and T. Meyer 10 / 16

22. RR 2014 Querying Temporal Databases via OWL 2 QL
SQL translation
• Translation from 2FO to SQL is straightforward using standard
techniques.
• In practice, the domain T must be represented as an explicit
relation RT in the database and used to guard temporal
quantifiers.
• The coalescing on the query-level is known to be inefficient. It is
usually better to apply it on the data-level.
S. Klarman and T. Meyer 11 / 16

23. RR 2014 Querying Temporal Databases via OWL 2 QL
Results: correctness
Theorem (Correctness of 2FO rewriting)
For every TBox T , temporal ABox A, TQL query ψ, and answer σ to ψ, it
holds that:
T , A |= σ(ψ) iff tdb(A) σ(ψ) 2FO.
Corollary (TQL queries are · -generic)
Whenever A = A then:
1 T , A |= σ(ψ) iff T , A |= σ(ψ),
2 tdb(A) σ(ψ) 2FO iff tdb(A ) σ(ψ) 2FO.
S. Klarman and T. Meyer 12 / 16

24. RR 2014 Querying Temporal Databases via OWL 2 QL
Results: data complexity
Theorem (Data complexity)
The data complexity of TQL query entailment over finite time domains is in
AC0
.
Note:
The finite domain restrictions is necessary to ensure that queries can be
effectively evaluated on TDBs considered as finite FO structures.
S. Klarman and T. Meyer 13 / 16

25. RR 2014 Querying Temporal Databases via OWL 2 QL
Results: combined complexity
Size of TQL queries:
The size of ψ 2FO is linear in the joint size of ψ and the FO rewritings
qT
1 , . . . , qT
n of the CQs embedded in ψ.
Theorem (Combined complexity)
The combined complexity of TQL query entailment over finite time domains
is PSPACE-complete.
• The result transfers from the entailment of Boolean FO queries
over relational databases.
• A PSPACE procedure cannot directly rely on the rewriting...
S. Klarman and T. Meyer 14 / 16

26. RR 2014 Querying Temporal Databases via OWL 2 QL
Results: combined complexity
Instead:
• compute and coalesce intermediate answers to all embedded CQs,
• and evaluate the query without rewriting the CQs.
RB(a, 1, 7)
RD(a, 6, 12)
RC(a, 3, 10)
Rq1
(a, 3, 7)
Rq2
(a, 6, 10)
RqT (a, 1, 10)coal
RC(a, 1, 3)
Rq1
(a, 1, 3)
RqT (a, 1, 3)
RqT (a, 3, 7)
RqT (a, 6, 10)
Rqi
RqT
RqT
coal
1 2 3 4 5 6 7 8 9 10 11 12
coal
[q(a)]([2,9])
A potentially better-behaved approach based on materialized view
maintenance: incremental, more responsive to updates.
S. Klarman and T. Meyer 15 / 16

27. RR 2014 Querying Temporal Databases via OWL 2 QL
Conclusions
Temporal query language:
• on the CQ / DL interface the approach only reuses existing
techniques and tools,
• the expressive power of temporal component subsumes LTL,
• satisfying FO rewriting properties.
Outlook:
• SQL translation must be further optimized (materialized view
maintenance; temp. joins and coalescing in the future ver. of SQL).
• Examine the links to other approaches to temporalizing OBDA.
S. Borgwardt, M. Lippmann, V. Thost. Temporal query answering in the description logic
DL-Lite. In: Proc. of FroCoS-13, 2013.
A. Artale, R. Kontchakov, F. Wolter, M. Zakharyaschev. Temporal description logic for
ontology-based data access. In: Proc. of IJCAI-13, 2013.
S. Klarman and T. Meyer 16 / 16