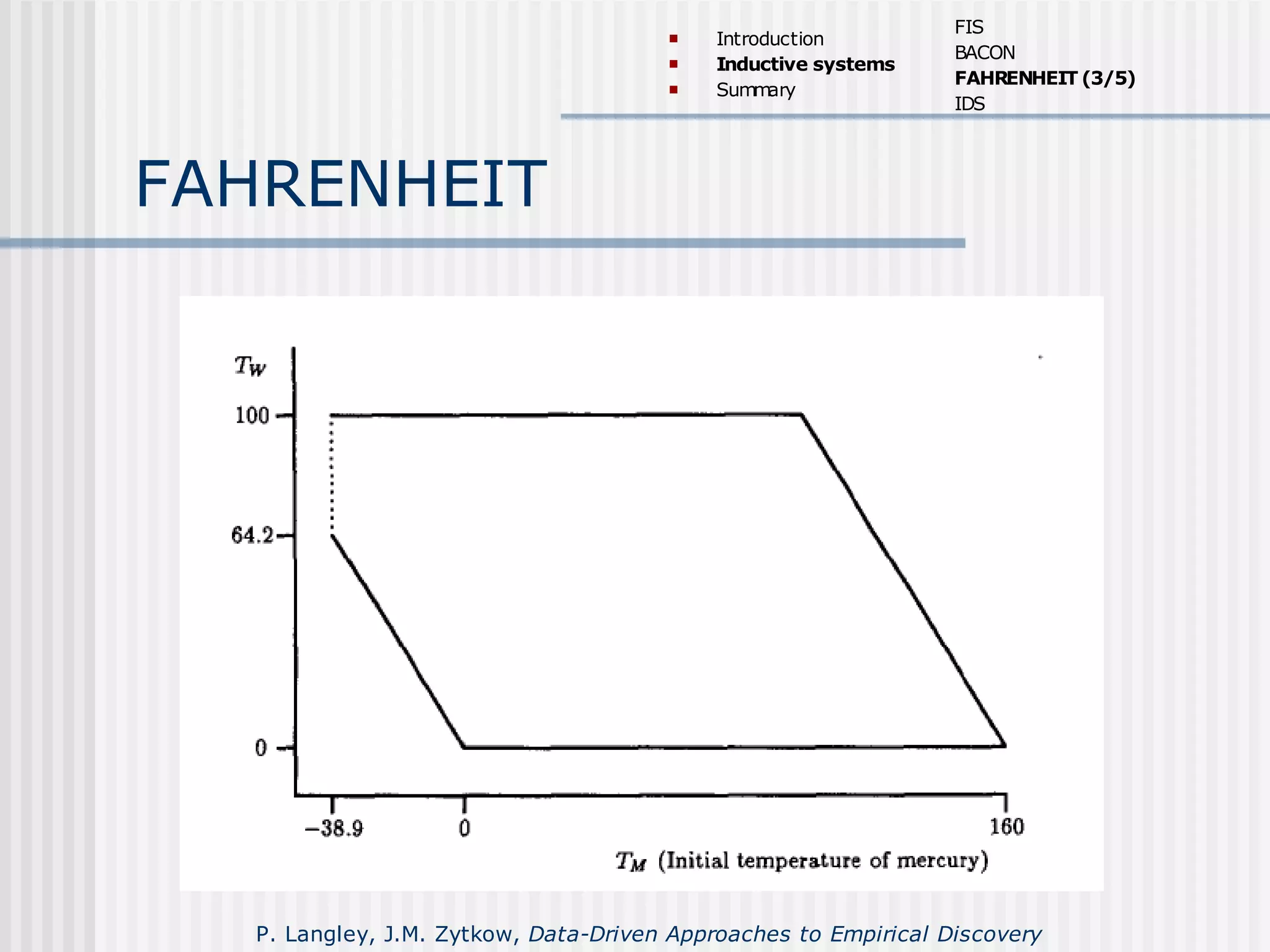
The document discusses several data-driven approaches to empirical discovery, including inductive machine systems. It describes the Function Induction System (FIS), BACON, FAHRENHEIT, and IDS systems. FIS used condition-action rules to detect patterns and recursively apply functions to residuals. BACON discovered laws relating independent and dependent terms using heuristics and defined new theoretical terms. FAHRENHEIT extended BACON by determining the scope of laws using separate numeric laws defining limits.

1. Data-Driven Approaches
to Empirical Discovery
Pat Langley
Jan M. Zytkow
Szymon Klarman
sklarman@science.uva.nl
December 6, 2006

2. Outline
 Introduction
 Basic Framework
 Logic of Scientific Discovery
 Inductive Systems
 Function Induction System
 BACON
 FAHRENHEIT
 IDS
 Summary
 Recap
 Final remarks
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

3. Empirical Discovery
Discovery as unsupervised learning
 Conceptual clustering
 Induction of descriptive regularities
 Providing good explanations
 Introduction
 Inductive systems
 Summary
Basic Framework
Logic of Scientific Discovery
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

4. Empirical Discovery
Discovery as unsupervised learning
 Conceptual clustering
 Induction of descriptive regularities
 Providing good explanations
Given: A set of observations or data.
Task: Find one or more general laws that
summarize these data.
 Introduction
 Inductive systems
 Summary
Basic Framework
Logic of Scientific Discovery
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

5. Machine Discovery
Features of machine discovery
systems:
 Defining theoretical terms
e.g. momentum as a product of mass and velocity
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery
 Introduction
 Inductive systems
 Summary
Basic Framework
Logic of Scientific Discovery

6. Machine Discovery
Features of machine discovery
systems:
 Defining theoretical terms
 Data-driven heuristics
 proposing laws
 defining new terms
 determining scope of laws
 Introduction
 Inductive systems
 Summary
Basic Framework
Logic of Scientific Discovery
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

7. Machine Discovery
Features of machine discovery
systems:
 Defining theoretical terms
 Data-driven heuristics
 Recursive application of used
methods
 Introduction
 Inductive systems
 Summary
Basic Framework
Logic of Scientific Discovery
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

8. Logic of Scientific Discovery
 Are there any rules directing the
process of scientific discovery?
 Can we find and formalize them?
 Introduction
 Inductive systems
 Summary
Basic Framework
Logic of Scientific Discovery
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

9. Inductive Machine...?
The question whether an inductive logic with exact rules is at all
possible is still controversial. But in one point the present
opinions of most philosophers and scientists seem to agree,
namely, that the inductive procedure is not, so to speak, a
mechanical procedure prescribed by fixed rules.
[...] it is not possible to construct an inductive machine [...], meant
as a mechanical contrivance that, when fed an observational
report, would furnish a suitable hypothesis, just as a computing
machine when supplied with two factors furnishes their product.
I am completely in agreement that an inductive machine
of this kind is not possible.
R. Carnap, Logical Foundations of Probability (1950)
 Introduction
 Inductive systems
 Summary
Basic Framework
Logic of Scientific Discovery
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

10. Inductive Machine...?
Induction is sometimes conceived as a method that leads, by
means of mechanically applicable rules, from observed facts to
corresponding general principles. In this case, the rules of
inductive inference would provide effective canons of scientific
discovery; [...]
Actually, however, no such general and mechanical
induction procedure is available at present; [...]. Nor
can the discovery of such a procedure ever be expected.
C.G. Hempel, Philosophy of Natural Science (1966)
 Introduction
 Inductive systems
 Summary
Basic Framework
Logic of Scientific Discovery
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

11. Inductive Systems
 Function Induction System (1974)
 BACON (1978)
 FAHRENHEIT (1986)
 IDS (1986)
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

12. Inductive Systems
 Function Induction System (1974)
 BACON (1978)
 FAHRENHEIT (1986)
 IDS (1986)
 Form of laws and theoretical terms discovered.
 Ability to determine the scope and context of laws.
 Ability to design experiments.
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

13. Function Induction System
Given: Set of <x,y> values.
Task: Inducing complex functions of one variable in
the presence of noisy data.
Primitive functions: ex/2
, x2
, x, x1/2
, lnx, sinx, cosx
Connectives: +, –, /, ×
e.g. y=x2
sinx–lnx
y=x/cosx
 Introduction
 Inductive systems
 Summary
FIS (1/3)
BACON
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

14. Function Induction System
Algorithm:
 Condition-action rules for detecting regularities
in the data.
 Each detected pattern suggests a class of
functions.
 If f is an assumed component of the overall
function than the set of residual data is created:
<x,y–f(y)>.
 The same method is applied to the set of
residuals.
 Halt when no more patterns can be detected.
 Introduction
 Inductive systems
 Summary
FIS (2/3)
BACON
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

15. Function Induction... – Evaluation
 Data-driven heuristics: pattern-detecting
condition-action rules.
 Component function as primitive forms of
theoretical terms.
 Recursive application of original heuristics.
 Functions of only one variable.
 Heuristics limited to fixed class of functions.
 Too simple to be applied to real-world tasks.
 Introduction
 Inductive systems
 Summary
FIS (3/3)
BACON
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

16. BACON
Given: Set of independent and dependent terms.
Task: Represent values of dependent terms by
means of independent ones.
Output:
 Simple numeric laws: X=8.32; U=1.57V
 Definitions of theoretical terms: X=Y/T
 Intrinsic properties like mass or specific heat of a
constant value for a particular object.
 Introduction
 Inductive systems
 Summary
FIS
BACON(1/5)
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

17. BACON
BACON
Example: The law of thermal contact conductance
World
simulator
Values of all
independent variables
The value of the
dependent variable
Independent: {M1, M2, T1, T2, Sub1, Sub2}
Dependent: {Tf}
1 1 1 2 2 2
1 1 2 2
f
c M T c M T
T
c M c M
+
=
+
 Introduction
 Inductive systems
 Summary
FIS
BACON(2/5)
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

18. BACON
Data collecting:
 All combinations of independent values in a directed
sequence fed to the ‘world simulator’.
Three heuristic rules:
 IF the values of X increase as the values of Y increase,
THAN define the ratio X/Y and examine its values.
 IF the values of X increase as the values of Y decrease,
THAN define the product XY and examine its values.
 IF the values of X are nearly constant for a number of
values, THAN hypothesize that X always has this value.
 Introduction
 Inductive systems
 Summary
FIS
BACON(3/5)
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

19. BACON
Tf=aT2+bTf=aT2+bT21
Laws impliedLaws foundTerm variedLevel
Discovering the law of thermal contact conductance
 Introduction
 Inductive systems
 Summary
FIS
BACON(4/5)
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

20. BACON
Tf=aT2+bTf=aT2+bT21
Tf=cT2+ dT1
a=c
b=dT1
T12
Laws impliedLaws foundTerm variedLevel
Discovering the law of thermal contact conductance
 Introduction
 Inductive systems
 Summary
FIS
BACON(4/5)
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

21. BACON
Tf=cT2+ dT1
a=c
b=dT1
T12
Tf=aT2+bTf=aT2+bT21
Tf= eM2T2/(M2-f)+
hT1/(M2-g)
M2=e(M2/c)+f
dM2=gd+h
M23
Laws impliedLaws foundTerm variedLevel
Discovering the law of thermal contact conductance
 Introduction
 Inductive systems
 Summary
FIS
BACON(4/5)
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

22. BACON
......M1, Sub2...
Tf= eM2T2/(M2-f)+
hT1/(M2-g)
M2=e(M2/c)+f
dM2=gd+h
M23
Tf=cT2+ dT1
a=c
b=dT1
T12
Tf=aT2+bTf=aT2+bT21
Tf=M2T2/(M2+(c1/
c2)M1)+(c1/c2)M1T1/
(M2+(c1/ c2)M1)
...Sub16
Laws impliedLaws foundTerm variedLevel
Discovering the law of thermal contact conductance
 Introduction
 Inductive systems
 Summary
FIS
BACON(4/5)
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

23. BACON – Evaluation
 Forms of the laws which can be discovered.
 Two basic forms of laws: simple constancies and linear
relations between two variables.
 That’s enough to cover many laws.
 Types of new terms which can be defined.
 Each newly defined term can be incorporated into
other terms later on.
 Intrinsic properties allow to transform nominal
variables into numeric ones.
 Determining the scope of the laws.
 Designing experiments.
 Introduction
 Inductive systems
 Summary
FIS
BACON(5/5)
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

24. BACON – Evaluation
 Forms of the laws which can be discovered.
 Types of new terms which can be defined.
 Determining the scope of the laws.
 Constant values for terms that haven’t been varied yet
– these are droped if the data merit such action.
 Designing experiments.
 Combinatorial design of experiments.
 Insensitivity to previously obtained results.
 Introduction
 Inductive systems
 Summary
FIS
BACON(5/5)
FAHRENHEIT
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

25. FAHRENHEIT
 The same heuristics for discovering laws as in
BACON.
 Scope of derived laws defined by separate
numeric laws.
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT (1/5)
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

26. FAHRENHEIT
 The same heuristics for discovering laws as in
BACON.
 Scope of derived laws defined by separate
numeric laws.
Example
Consider the following setting:
Sub1=‘water’, Sub2=‘mercury’, M1=0.1kg, M2=5kg
Tf=jTM+kTW
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT (1/5)
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

27. FAHRENHEIT
TM max, TM minTf=aTM+b1
Scope of lawsLaws impliedLevel
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT (2/5)
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

28. FAHRENHEIT
TM max=-0.6TW+160
TM min=-0.6TW
Tf=cTM+ dTW2
TM max, TM minTf=aTM+b1
Scope of lawsLaws impliedLevel
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT (2/5)
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

29. FAHRENHEIT
TM max=-0.6TW+160
TM min=-0.6TW
TW max1, TW min1
TW max2, TW min2
Tf=cTM+ dTW2
TM max, TM minTf=aTM+b1
Scope of lawsLaws impliedLevel
 Upper and lower limits on the higher-level laws.
 Laws that express upper and lower limits as
functions of other terms.
 Limits on these limit-based laws themselves.
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT (2/5)
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

30. FAHRENHEIT
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT (3/5)
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

31. FAHRENHEIT
Other interesting features:
 Good handling of the irrelevant attributes in the
experiment design.
 Attributes once discovered to be irrelevant are skipped
in further experiments.
 Robust to the order of varying variables.
 Backtracking and experimenting with alternative
orders of variables in case of failure.
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT (4/5)
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

32. FAHRENHEIT – Evaluation
 Providing numeric context for validity of laws.
 More intelligent data gathering.
 More sophisticated heuristics.
 Ignores the qualitative structure of phenomena
being described.
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT (5/5)
IDS
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

33. ISD
Integrated System of Discovery
 Formulates both qualitative laws and discovers
numeric relations.
 Differences in representations of laws and in the
discovery process.
 More complex ‘world simulator’ for gathering-
data:
 All atrribute-value pairs associated with specific
objects.
 The values of attributes change over time.
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT
IDS (1/5)
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

34. ISD
Qualitative schema for the heat conductance law:
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT
IDS (2/5)
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

35. ISD
Constructing the qualitative schemas:
 Built-in set of primitive schemas (e.g. schema
for heating, schema for placing objects)
 Rules of creating new schemas:
 IF new behavior encountered THEN create a new state
in the schema.
 IF a known state is encountered which hasn’t been
predicted THEN add a connection between this state
and the previous one.
 IF a state is overly general THEN specify its
description.
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT
IDS (3/5)
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

36. ISD
Representation of laws in qualitative
schemas:
,1 ,1
,3 ,3
A A A B B B
A B
A A B B
c M T c M T
T T
c M c M
+
= =
+
Benefits of qualitative schemas:
 Providing context within which the law has
meaning.
 Constraining the search of numeric laws
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT
IDS (4/5)
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

37. ISD – Evaluation
 Greater representational power.
 Providing more context for numeric laws.
 Scope laws not defined.
 Alternative orders of variables not considered.
 Introduction
 Inductive systems
 Summary
FIS
BACON
FAHRENHEIT
IDS (5/5)
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

38. Recap
 Providing qualitative contexts determining
validity of laws.IDS

 Providing numerical constraints for
determining scope of laws.FAHRENHEIT

 Relating many independent variables to a
dependent one.
 Designing combinatorial experiments.
 Defining new terms.
BACON

 Set of primitive functions.
 Condition-action rules for inducing
complex functions.

Function
Induction
System
 Introduction
 Inductive systems
 Summary
Recap
Final Remarks
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery

39. Further Philosophical Issues
 Machine discovery systems may provide
computational models of the historical discovery
process.
 They may also provide normative standards to
direct the process of scientific discovery.
 When is a machine discovery system successful?
 When it can rediscover many known laws?
 When it can replay the evolution of some discoveries?
 When it can derive new, useful laws?
 Introduction
 Inductive systems
 Summary
Recap
Final Remarks
P. Langley, J.M. Zytkow, Data-Driven Approaches to Empirical Discovery