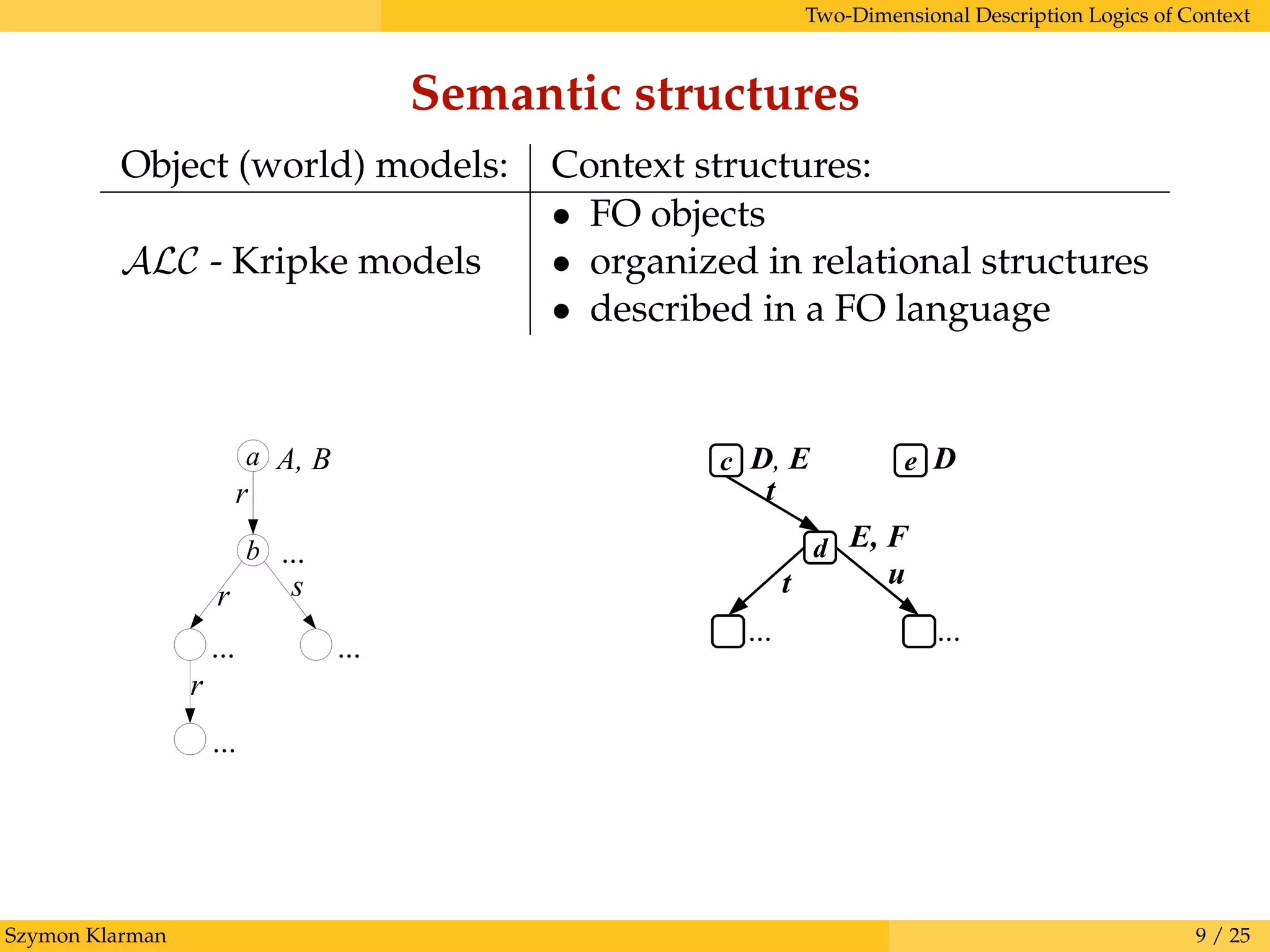
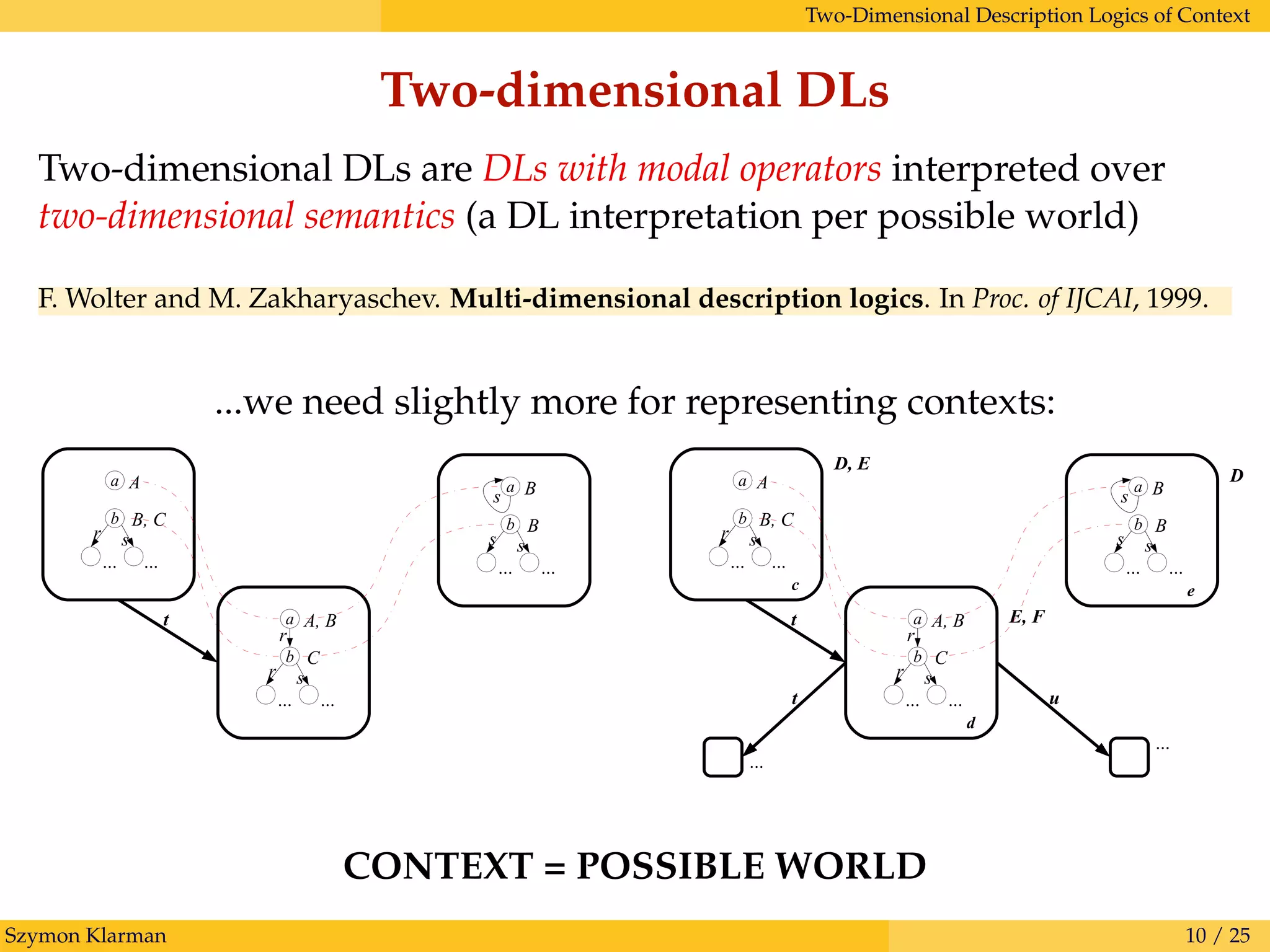
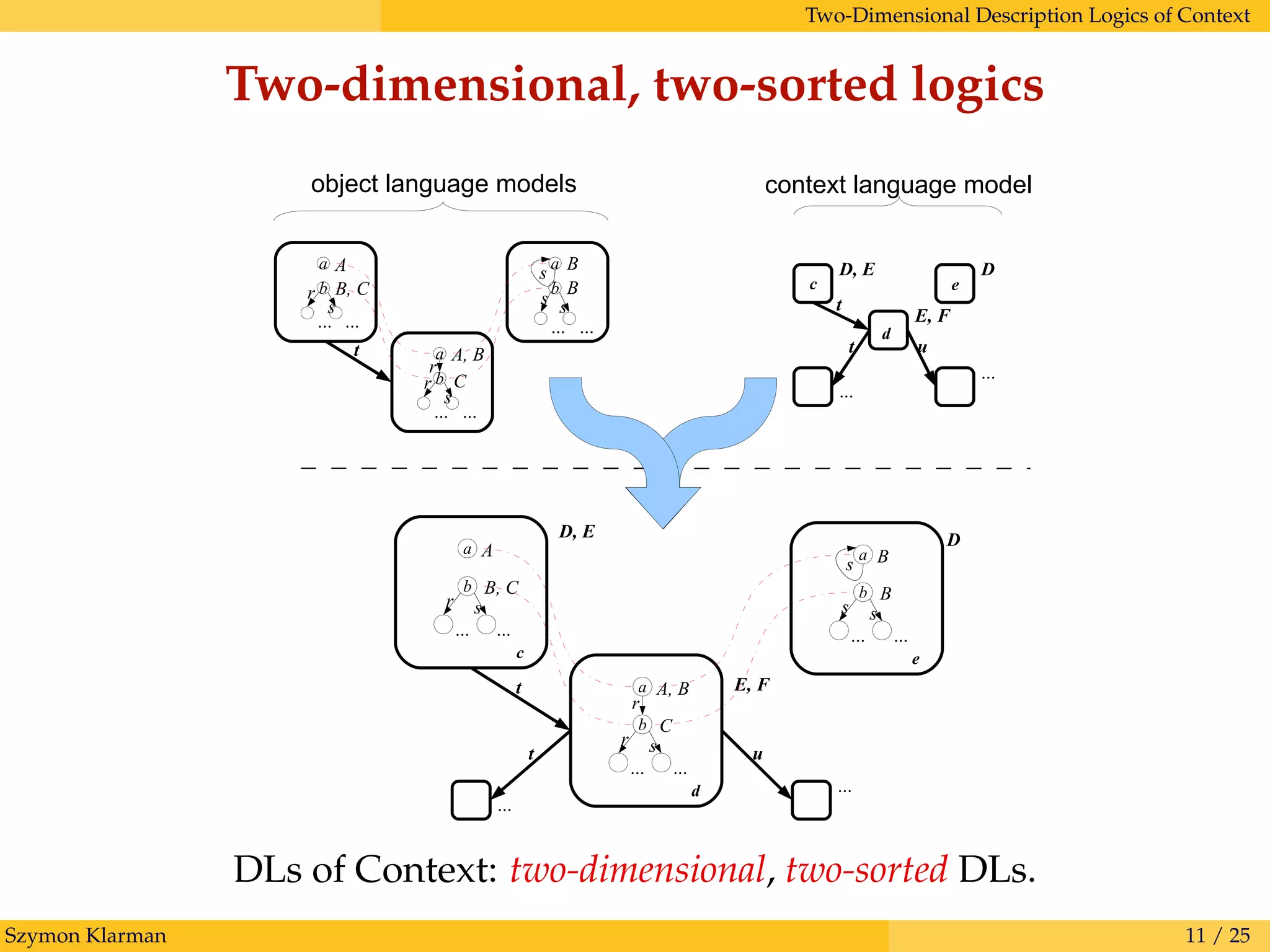
This document discusses representing knowledge with contexts in description logics. It proposes two-dimensional, two-sorted description logics of context that include: 1. Separate context and object languages to describe contexts and knowledge respectively. 2. Contexts represented as first-order objects that can be organized into relational structures and described in the context language. 3. A two-dimensional semantics where each possible world has its own description logic interpretation, allowing for alternative viewpoints.

1. Two-Dimensional Description Logics of Context
Szymon Klarman
joint work with V´ıctor Guti´errez-Basulto
Centre for Artificial Intelligence Research
CSIR Meraka Institute & University of KwaZulu-Natal
South Africa
November 26, 2014
Dresden

2. Two-Dimensional Description Logics of Context
Contextuality of knowledge
Szymon Klarman 1 / 25
The International
Squared Earth Society
(www.rogermwilcox.com/...)
The Earth is flat and squared.
The International
Flat Earth Society
(www.theflatearthsociety.org)
The Earth is a (flat) disk.

3. Two-Dimensional Description Logics of Context
Contextuality of knowledge
Szymon Klarman 2 / 25
The Earth is flat and squared.The Earth is a (flat) disk.

4. Two-Dimensional Description Logics of Context
Contextuality of knowledge
Szymon Klarman 2 / 25
The Earth is flat and squared.The Earth is a (flat) disk.
DISK(earth)

5. Two-Dimensional Description Logics of Context
Contextuality of knowledge
Szymon Klarman 2 / 25
The Earth is flat and squared.The Earth is a (flat) disk.
DISK(earth)
DISK FLAT CIRCULAR

6. Two-Dimensional Description Logics of Context
Contextuality of knowledge
Szymon Klarman 2 / 25
The Earth is flat and squared.
FLAT(earth)
SQUARED(earth)
The Earth is a (flat) disk.
DISK(earth)
DISK FLAT CIRCULAR

7. Two-Dimensional Description Logics of Context
Contextuality of knowledge
Szymon Klarman 2 / 25
The Earth is flat and squared.
FLAT(earth)
SQUARED(earth)
SQUARED ¬CIRCULAR
The Earth is a (flat) disk.
DISK(earth)
DISK FLAT CIRCULAR

8. Two-Dimensional Description Logics of Context
Contextuality of knowledge
Szymon Klarman 2 / 25
The Earth is flat and squared.
FLAT(earth)
SQUARED(earth)
SQUARED ¬CIRCULAR
The Earth is a (flat) disk.
DISK(earth)
DISK FLAT CIRCULAR
FLAT(earth)
CIRCULAR(earth)

9. Two-Dimensional Description Logics of Context
Contextuality of knowledge
Szymon Klarman 2 / 25
The Earth is flat and squared.
FLAT(earth)
SQUARED(earth)
SQUARED ¬CIRCULAR
¬CIRCULAR(earth)
The Earth is a (flat) disk.
DISK(earth)
DISK FLAT CIRCULAR
FLAT(earth)
CIRCULAR(earth)

10. Two-Dimensional Description Logics of Context
Contextuality of knowledge
Szymon Klarman 2 / 25
CIRCULAR ¬CIRCULAR(earth)
The Earth is flat and squared.
FLAT(earth)
SQUARED(earth)
SQUARED ¬CIRCULAR
¬CIRCULAR(earth)
The Earth is a (flat) disk.
DISK(earth)
DISK FLAT CIRCULAR
FLAT(earth)
CIRCULAR(earth)

11. Two-Dimensional Description Logics of Context
Contextuality of knowledge
Szymon Klarman 2 / 25
CIRCULAR ¬CIRCULAR(earth)
Reasoning out of context!
The Earth is flat and squared.
FLAT(earth)
SQUARED(earth)
SQUARED ¬CIRCULAR
¬CIRCULAR(earth)
The Earth is a (flat) disk.
DISK(earth)
DISK FLAT CIRCULAR
FLAT(earth)
CIRCULAR(earth)

12. Two-Dimensional Description Logics of Context
Representing and reasoning with contexts
Szymon Klarman 3 / 25
DISK(earth)

13. Two-Dimensional Description Logics of Context
Representing and reasoning with contexts
Szymon Klarman 3 / 25
DISK(earth)

14. Two-Dimensional Description Logics of Context
Representing and reasoning with contexts
Szymon Klarman 3 / 25
c1
DISK(earth)

15. Two-Dimensional Description Logics of Context
Representing and reasoning with contexts
Szymon Klarman 3 / 25
c1
DISK(earth)
statuteOf(c1, ifes)

16. Two-Dimensional Description Logics of Context
Representing and reasoning with contexts
Szymon Klarman 3 / 25
a
FLAT(earth)
SQUARED(earth)
statuteOf(c2, ises)
refersTo
c2c1
DISK(earth)
statuteOf(c1, ifes)

17. Two-Dimensional Description Logics of Context
Overview
Motivation:
Contexts are essential in KR.
Goal:
Define a principled and generic DL of contexts.
Two foundations:
• McCarthy’s theory of contexts (conceptual),
• two-dimensional DLs (logical).
Results:
• a family of two-dimensional, two-sorted formalisms,
• complexity results for different logics in the family.
Szymon Klarman 4 / 25

18. Two-Dimensional Description Logics of Context
Preliminaries
A Description Logic ontology:
TBox: ∃orbits.PLANET SATELLITE
PLANETINSOLARSYSTEM PLANET ∃orbits.{Sun}
ABox: PLANETINSOLARSYSTEM(Earth), orbits(Moon, Earth)
• the semantics given in terms of Kripke models I = (∆I, ·I),
• the axioms of an ontology must hold in all possible models,
• hence, they impose a global, uniform view on the domain,
• hence, no alternative viewpoints are possible...
Szymon Klarman 5 / 25

19. Two-Dimensional Description Logics of Context
Why KR needs contexts
Bouquet et al. distinguish 2 theories of contexts in KR:
divide-and-conquer: “[...] there is something like a global theory of the
world. This global theory has an internal structure, and this structure
is articulated into a collection of contexts.”
⇒ Large ontologies with maximum coverage (SNOMED, CYC).
→ ad-hoc contextualization mechanisms.
Szymon Klarman 6 / 25

20. Two-Dimensional Description Logics of Context
Why KR needs contexts
Bouquet et al. distinguish 2 theories of contexts in KR:
divide-and-conquer: “[...] there is something like a global theory of the
world. This global theory has an internal structure, and this structure
is articulated into a collection of contexts.”
⇒ Large ontologies with maximum coverage (SNOMED, CYC).
→ ad-hoc contextualization mechanisms.
compose-and-conquer: “[...] there is not such a thing as a global theory of
the world, but only many local theories. Each local theory represents a
viewpoint on the world. Also, there may exist relations between local
theories that allow a reasoner to (partially) compose them into a more
comprehensive view.”
⇒ Ontology integration/linking.
→ Distributed DLs, Package DLs, E-connections...
Szymon Klarman 6 / 25

21. Two-Dimensional Description Logics of Context
What is a context?
A context is:
• “any information that can be used to characterize the situation of
an entity.”
• “a context is the whole of relevant information about the situation
in which a certain piece of knowledge is true, necessary for a
correct and complete interpretation of this knowledge.”
Szymon Klarman 7 / 25

22. Two-Dimensional Description Logics of Context
What is a context?
A context is:
• “any information that can be used to characterize the situation of
an entity.”
• “a context is the whole of relevant information about the situation
in which a certain piece of knowledge is true, necessary for a
correct and complete interpretation of this knowledge.”
“Context” is a very context-dependent notion...
Szymon Klarman 7 / 25

23. Two-Dimensional Description Logics of Context
McCarthy’s theory of contexts
1 Contexts are formal objects.
• ist(c, p) = proposition p is true in context c,
• e.g., ist(Hamlet, ‘Hamlet is a prince.’).
2 Contexts can be described in a first-order language.
• ∀x(C(x) → ist(x, p)) = p is true in every context of type C,
• e.g., ∀x(barbershop(x) → ist(x, ‘Main service is a haircut.’)).
3 Contexts are organized in relational structures.
• ist(c, ist(c , p)) = it is true in c that ist(c , p),
• e.g., ist(France, ist(capital, ‘The city river is Seine.’)).
J. McCarthy. Generality in Artificial Intelligence. In: Communic. of the ACM, 1987.
R. Guha. Contexts: a formalization and some applications. PhD thesis, 1991.
S. Buvaˇc. Quantificational Logic of Context. In: Proc. of AAAI, 1996.
Szymon Klarman 8 / 25

24. Two-Dimensional Description Logics of Context
Semantic structures
Object (world) models: Context structures:
Szymon Klarman 9 / 25

25. Two-Dimensional Description Logics of Context
Semantic structures
Object (world) models: Context structures:
ALC - Kripke models
a
b
r
r s
r
...
... ...
...
A, B
Szymon Klarman 9 / 25

26. Two-Dimensional Description Logics of Context
Semantic structures
Object (world) models: Context structures:
• FO objects
ALC - Kripke models
a
b
r
r s
r
...
... ...
...
A, B
Szymon Klarman 9 / 25

27. Two-Dimensional Description Logics of Context
Semantic structures
Object (world) models: Context structures:
• FO objects
ALC - Kripke models • organized in relational structures
a
b
r
r s
r
...
... ...
...
A, B
t
t u
Szymon Klarman 9 / 25

28. Two-Dimensional Description Logics of Context
Semantic structures
Object (world) models: Context structures:
• FO objects
ALC - Kripke models • organized in relational structures
• described in a FO language
a
b
r
r s
r
...
... ...
...
A, B
t
t u
E, F
... ...
D, E Dc
d
e
Szymon Klarman 9 / 25

29. Two-Dimensional Description Logics of Context
Semantic structures
Object (world) models: Context structures:
• FO objects
ALC - Kripke models • organized in relational structures
• described in a FO language
D
t
u
D, E
a
b
r
r s
... ...
d
...
a
b
r s
... ...
c
a
b
s s
B
... ...
B
e
t
s
...
E, F
C
A, B
B, C
A
Szymon Klarman 9 / 25

30. Two-Dimensional Description Logics of Context
Two-dimensional DLs
Two-dimensional DLs are DLs with modal operators interpreted over
two-dimensional semantics (a DL interpretation per possible world)
F. Wolter and M. Zakharyaschev. Multi-dimensional description logics. In Proc. of IJCAI, 1999.
t a
b
r
r s
... ...
a
b
r s
... ...
a
b
s s
B
... ...
Bs
C
A, B
B, C
A
CONTEXT = POSSIBLE WORLD
Szymon Klarman 10 / 25

31. Two-Dimensional Description Logics of Context
Two-dimensional DLs
Two-dimensional DLs are DLs with modal operators interpreted over
two-dimensional semantics (a DL interpretation per possible world)
F. Wolter and M. Zakharyaschev. Multi-dimensional description logics. In Proc. of IJCAI, 1999.
...we need slightly more for representing contexts:
t a
b
r
r s
... ...
a
b
r s
... ...
a
b
s s
B
... ...
Bs
C
A, B
B, C
A D
t
u
D, E
a
b
r
r s
... ...
d
...
a
b
r s
... ...
c
a
b
s s
B
... ...
B
e
t
s
...
E, F
C
A, B
B, C
A
CONTEXT = POSSIBLE WORLD
Szymon Klarman 10 / 25

32. Two-Dimensional Description Logics of Context
Two-dimensional, two-sorted logics
D
t
u
D, E
a
b
r
r s
... ...
d
...
a
b
r s
... ...
c
a
b
s s
B
... ...
B
e
t
s
...
E, F
C
A, B
B, C
A
t
u
D, E
d
c e
t
...
E, F
D
...
context language modelobject language models
D
t a
b
r
r
s
... ...
a
br
s
... ...
a
b
s s
B
... ...
Bs
C
A, B
B, C
A
DLs of Context: two-dimensional, two-sorted DLs.
Szymon Klarman 11 / 25

33. Two-Dimensional Description Logics of Context
DLs of Context: syntax
Two sorts of languages:
• LC: context language over vocabulary Γ
• LO: object language over vocabulary Σ
KB K = (C, O) consists of a context ontology C and an object ontology O.
Context language:
A usual DL, e.g., EL, ALC, SROIQ.
Country(france)
neighbor(france, germany)
Object language:
A DL closed under context operators, and with contextualized axioms.
Szymon Klarman 12 / 25

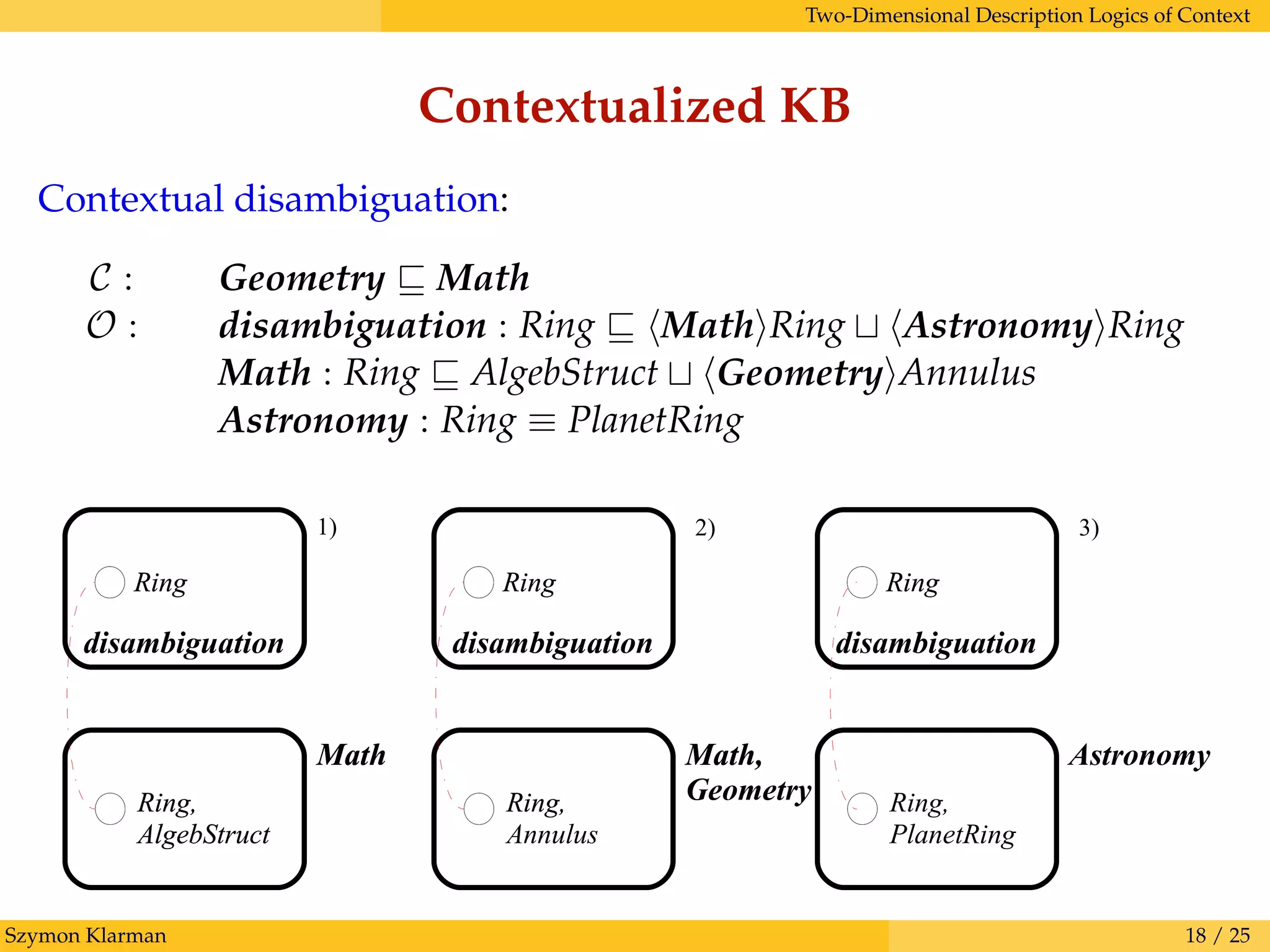
34. Two-Dimensional Description Logics of Context
Context operators
Context operators are Kn-like modalities involving context descriptions:
r.C D | [r.C] D
where r is a context role, C a context concept and D an object concept.
Examples:
e.g.: neighbor.Country Citizen:
neighbor
a a : Citizen: 〈neighbor.Country〉 Citizen
: Countryc
Szymon Klarman 13 / 25

35. Two-Dimensional Description Logics of Context
Contextualized axioms
Two types of contextualized object axioms:
• c : ϕ ϕ is true in context c, e.g.:
germany : ∃hasParent.Citizen(john)
france : neighbor.Country Citizen NoVisaRequirement
• C : ϕ ϕ is true in every context of type C, e.g.:
Country : ∃hasParent.Citizen Citizen
where c is context name, C is a context concept and ϕ is an object
axiom.
Szymon Klarman 14 / 25

36. Two-Dimensional Description Logics of Context
Contextualized KB
Visa requirements in different countries:
C : Country(germany)
neighbor(france, germany)
O : germany : ∃hasParent.Citizen(john)
Country : ∃hasParent.Citizen Citizen
france : neighbor.Country Citizen NoVisaRequirement
neighbor
j j
NoVisaRequirement
Country
NoVisaRequirement
Citizen
Citizenfrance germany
hasParent
(*) j = john
We can capture divide-and-conquer scenarios.
Szymon Klarman 15 / 25

37. Two-Dimensional Description Logics of Context
DLs of Context: semantics
A model of a KB K = (C, O) is a composition of two interpretations.
M = (C, ·J , ∆, {·I(i)}i∈C)
...
t
u
D, E
d
c e
t
...
E, F
D
context language model object language models
t a
b
r
r
s
... ...
a
br
s
... ...
a
b
s s
B
... ...
Bs
C
A, B
B, C
A
Where:
• ϕ ∈ C is satisfied iff it is satisfied in J ,
• c : ϕ ∈ O is satisfied iff ϕ is satisfied in (∆, ·I(cJ
)
),
• C : ϕ ∈ O is satisfied iff for every i ∈ CJ
, ϕ is satisfied in (∆, ·I(i)
),
• ( r.C D)I(i)
= {x | ∃j ∈ C : (i, j) ∈ rJ
∧ j ∈ CJ
∧ x ∈ DI(j)
}.
Szymon Klarman 16 / 25
J = (C, ·J ) I = (C, ∆, {·I(i)}i∈C)

38. Two-Dimensional Description Logics of Context
Alternative context operators
We can also use S5-like modalities with context descriptions:
C D | [C] D
where r is a context role, C a context concept and D an object concept.
E.g., HumanAnatomy Heart:
a a HeartHumanAnatomy Heart
HumanAnatomy
c
Semantics: ( C D)I(i) = {x | ∃j ∈ C : j ∈ CJ
∧ x ∈ DI(j)}.
Szymon Klarman 17 / 25

39. Two-Dimensional Description Logics of Context
Contextualized KB
Contextual disambiguation:
C : Geometry Math
O : disambiguation : Ring Math Ring Astronomy Ring
Math : Ring AlgebStruct Geometry Annulus
Astronomy : Ring ≡ PlanetRing
Math
Ring
disambiguation
Ring,
AlgebStruct
1)
Math
Ring
Ring,
AlgebStruct
Math
Ring
disambiguation
Ring,
Annulus
Math,
Geometry
Ring
Ring,
Ring
Astronomy
Ring
disambiguation
Ring,
PlanetRing
2) 3)
Szymon Klarman 18 / 25

40. Two-Dimensional Description Logics of Context
Interoperability constraints
We can also capture compose-and-conquer scenarios:
• each ontology associated with a unique context,
• finite domain of contexts,
• context language used for representing meta-data.
C : HumanAnatomy(c)
Anatomy(d)
HumanAnatomy Anatomy
O : c : Heart(a)
: HumanAnatomy Heart [Anatomy]HumanHeart
a Heart
HumanAnatomy
a
Anatomy
dc
Szymon Klarman 19 / 25

41. Two-Dimensional Description Logics of Context
Interoperability constraints
We can also capture compose-and-conquer scenarios:
• each ontology associated with a unique context,
• finite domain of contexts,
• context language used for representing meta-data.
C : HumanAnatomy(c)
Anatomy(d)
HumanAnatomy Anatomy
O : c : Heart(a)
: HumanAnatomy Heart [Anatomy]HumanHeart
a Heart
HumanAnatomy,
Anatomy
a
Anatomy
dc
Szymon Klarman 19 / 25

42. Two-Dimensional Description Logics of Context
Interoperability constraints
We can also capture compose-and-conquer scenarios:
• each ontology associated with a unique context,
• finite domain of contexts,
• context language used for representing meta-data.
C : HumanAnatomy(c)
Anatomy(d)
HumanAnatomy Anatomy
O : c : Heart(a)
: HumanAnatomy Heart [Anatomy]HumanHeart
a Heart,
HumanHeart
HumanAnatomy,
Anatomy
a
Anatomy
HumanHeart
dc
Szymon Klarman 19 / 25

43. Two-Dimensional Description Logics of Context
Ontology mappings
We can use functional modalities to represent mappings:
c: Patient ∃hasPart. {d} HumanHeart
c: Patient(a)
d: HumanHeart Heart
d: Heart Organ
a
b
a
b
HumanHeart,
Heart, Organ
Patient
c d
〈d〉 HumanHeart
hasPart
Patient
Szymon Klarman 20 / 25

44. Two-Dimensional Description Logics of Context
Complexity
Complexity results for the KB satisfiability problem in DLCs with...
• ...K-like context operators:
LO / LC EL ALC − SHOI
ALC 2EXPTIME-complete 2EXPTIME-complete
SHOI 2EXPTIME-complete 2EXPTIME-complete
S. Klarman and V. Guti´errez-Basulto. ALCALC: a Context DL. In Proc. of JELIA, 2010.
S. Klarman and V. Guti´errez-Basulto. Description Logics of Context. In Journal of Logic and
Computation, in press.
• ...S5-like context operators:
LO / LC EL ALC, ALCO
EL PTIME EXPTIME-hard
ALC EXPTIME-complete NEXPTIME-complete
ALCO NEXPTIME-complete NEXPTIME-complete
S. Klarman and V. Guti´errez-Basulto. Two-Dimensional Description Logics for Context-Based
Semantic Interoperability. In Proc. of AAAI, 2011.
Szymon Klarman 21 / 25

45. Two-Dimensional Description Logics of Context
2EXPTIME-completeness
Decision problem: concept satisfiability w.r.t. global TBoxes: given a object
concept C and a global object TBox T (i.e., for every ϕ ∈ T , ϕ holds in
every context) decide whether there is a model of T satisfying C.
ALC EXPTIME-complete
(DAltn)ALC 2EXPTIME-complete
(Kn)ALC . . .
ALCALC 2EXPTIME-complete
ALCALC with rigid roles undecidable
Upper bound: a variant of type elimination procedure.
Szymon Klarman 22 / 25

46. Two-Dimensional Description Logics of Context
Lower Bound
Lower bound: word problem for exponentially-space bounded
Alternating Turing Machine.
a
a b ∅
DAlt-world with d∈Tape
DAlt-world with d∉Tape
2n
tape cell containing “a”
b
...
a
a
accessibility relation of a
a b ∅
a b ∅
a b ∅
a b ∅
a b ∅
a
b
∅
∅
ATM transitions along DAlt transition modalities
ATM tapes along DAlt alphabet modalities
2n
Szymon Klarman 23 / 25

47. Two-Dimensional Description Logics of Context
Conclusions
DLs of Context are extensions of DLs, which:
• have good formal foundations: conceptual (McCarthy) and logical
(two-dimensional DLs),
• are generic enough to capture and support diverse forms of
contextualization in the DL framework,
• have some computationally well-behaved fragments, e.g., with
S5-like operators.
What constitutes a context in DLCs is an application-driven choice.
DLC contexts are like DL individuals:
a context/individual =
a situation/object in the application domain worth representing.
A context/individual description =
knowledge about this situation/object worth representing.
Szymon Klarman 24 / 25

48. Two-Dimensional Description Logics of Context
Interesting problems
• To what extent can we restate core notions of different
context-based systems in the framework?
⇒ lifting, bridge rules, generality-specificity hierarchy,
entering/exiting, detecting...
• Are there interesting restricted settings that could benefit from
DLCs?
⇒ model checking contextualized KBs instead of representing
them...
• Can this methodology be extended towards other
two-dimensional DLs?
⇒ temporal, spatial...
Szymon Klarman 25 / 25