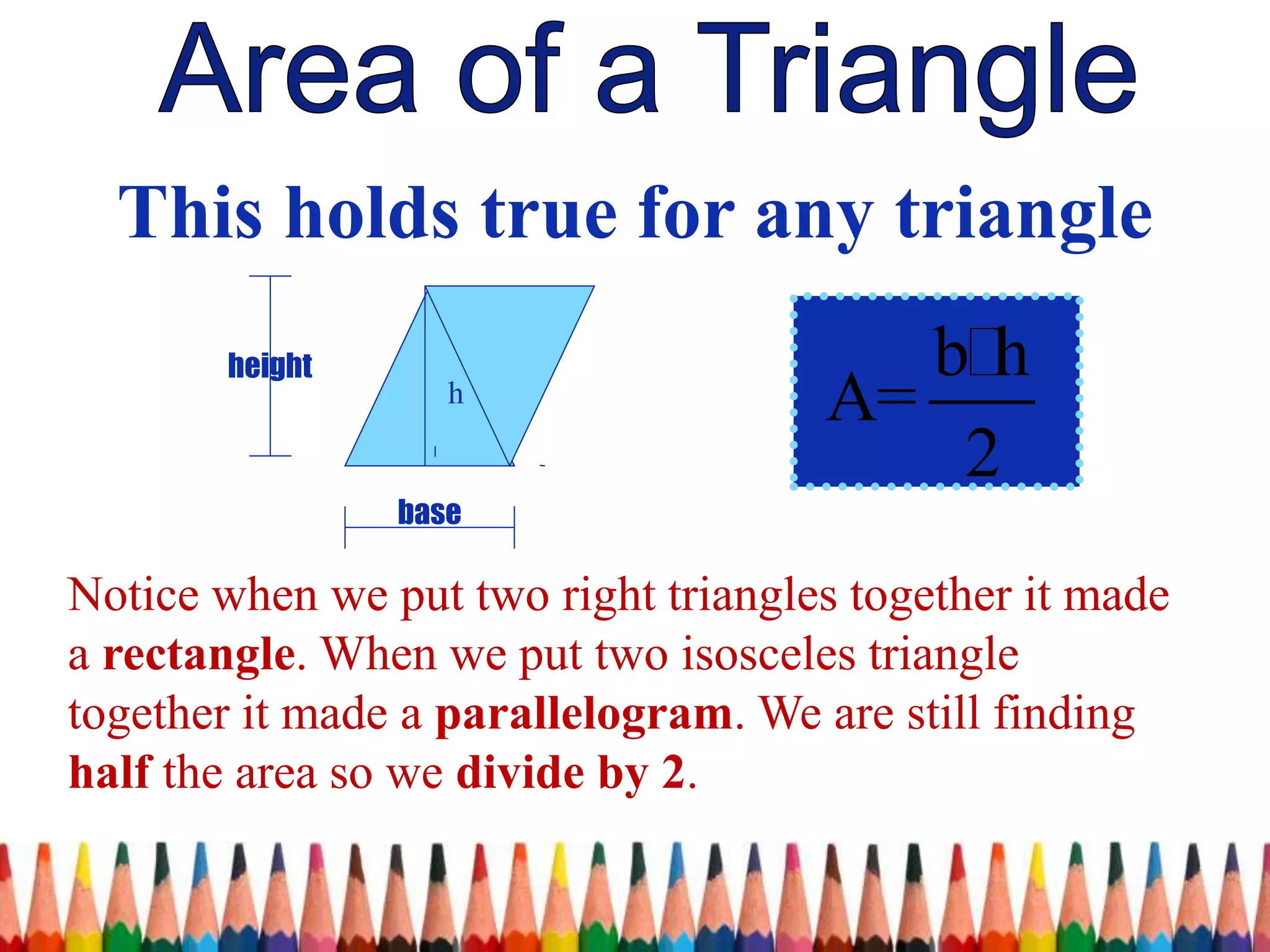
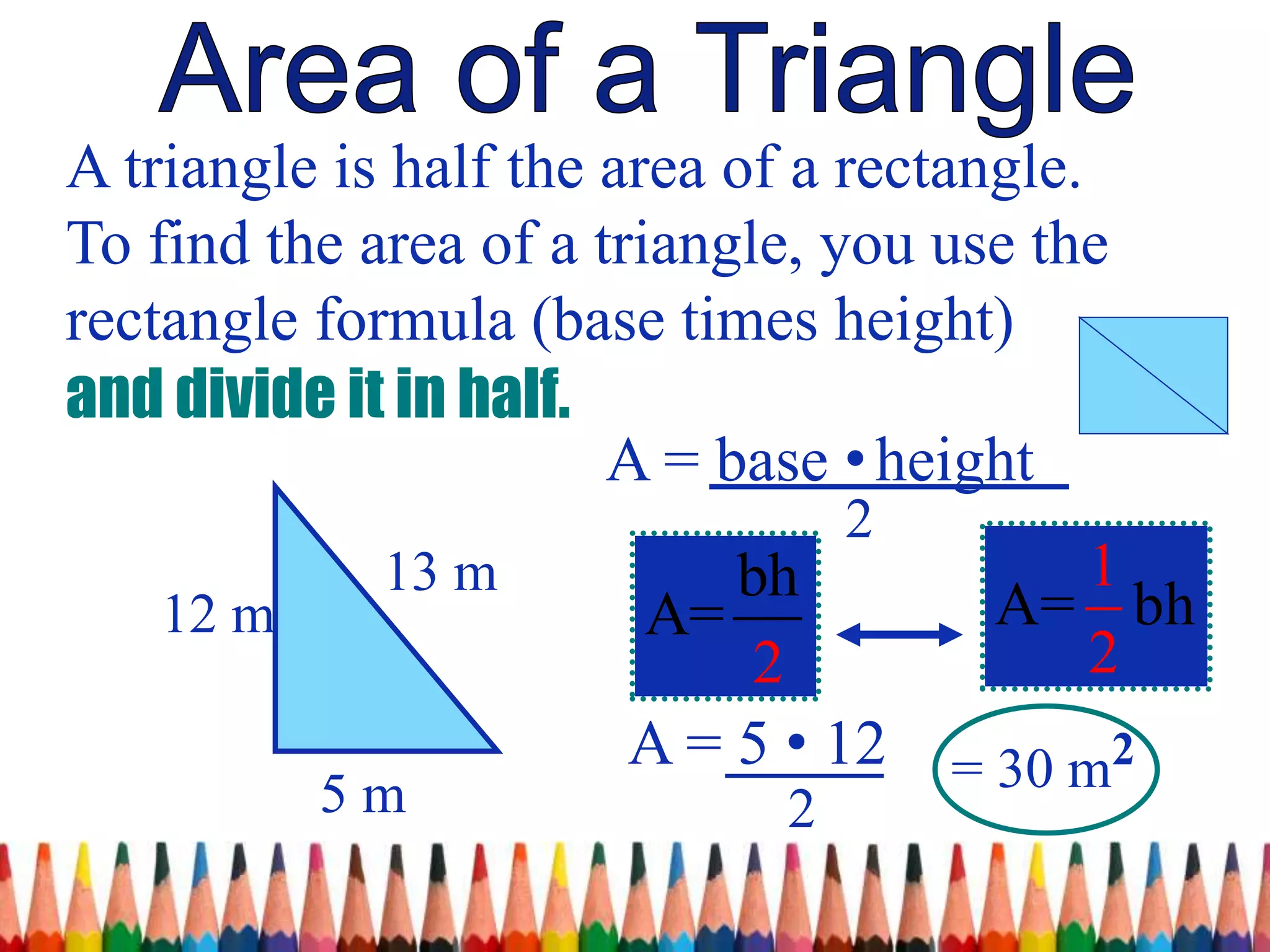
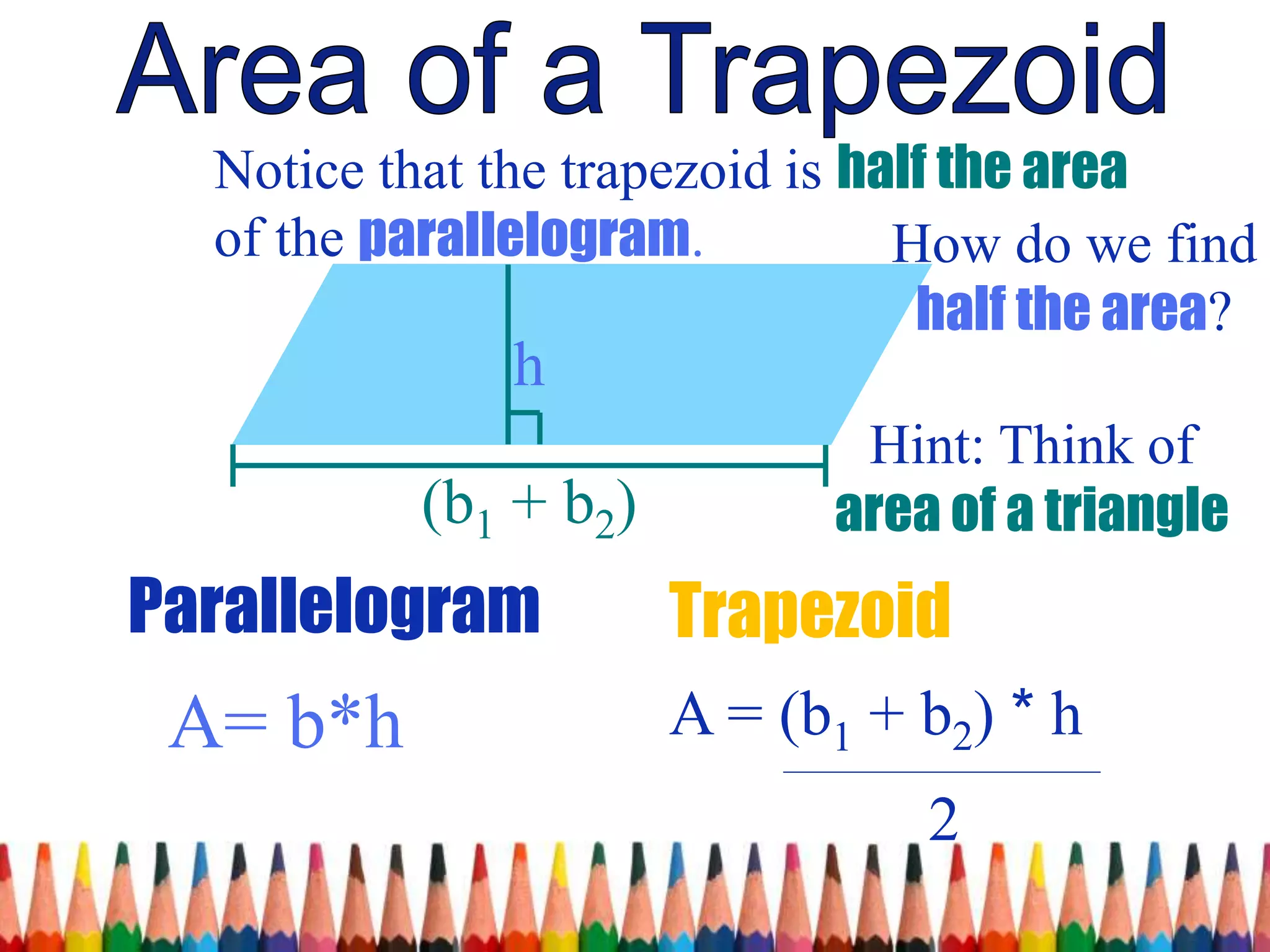
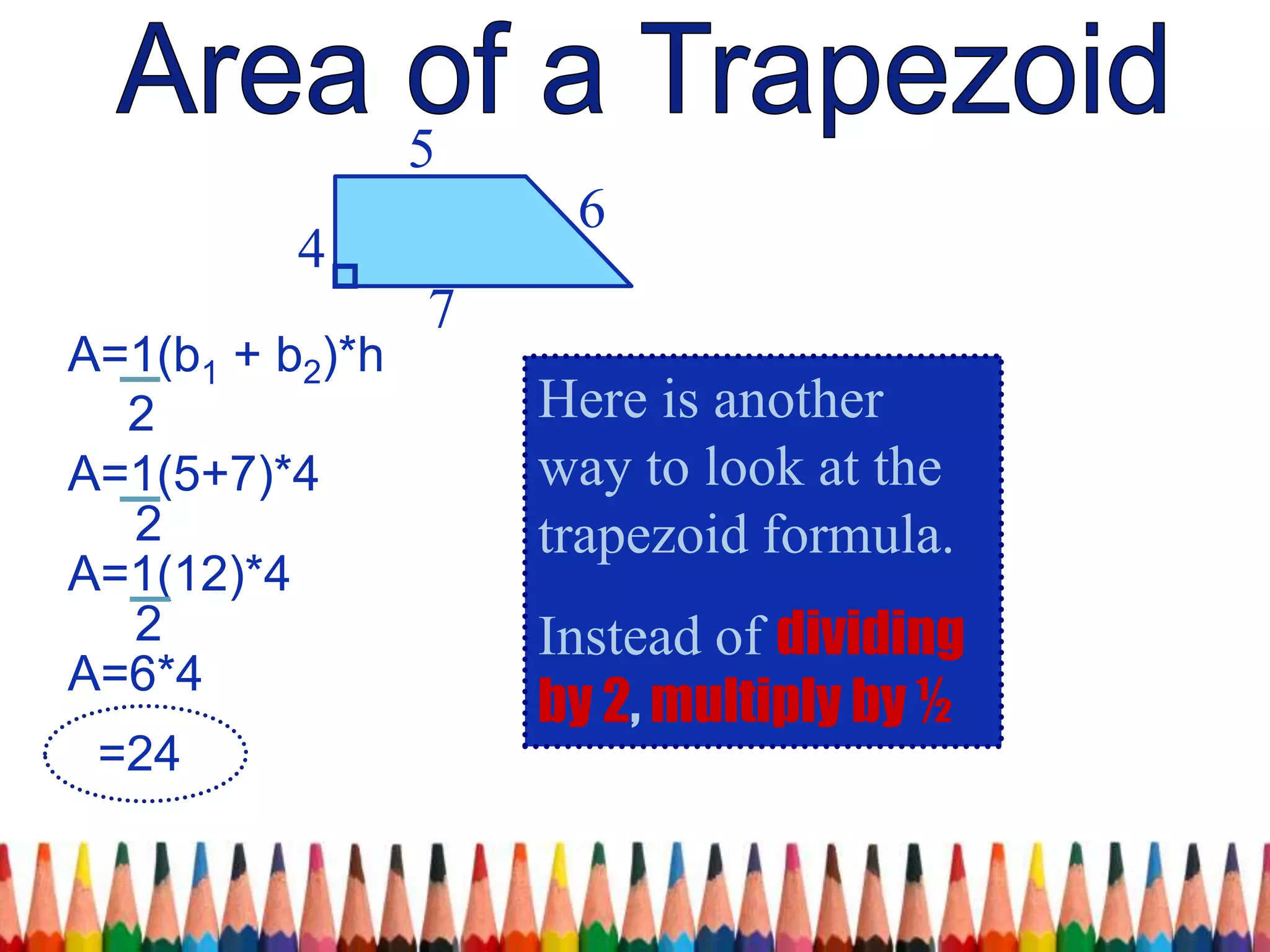
The document discusses the derivation of the formula for the area of a trapezoid. It begins by reviewing the formulas for the area of a triangle and parallelogram. It then shows that two trapezoids joined together form a parallelogram. Since a parallelogram's area is (base 1 + base 2) * height, and two trapezoids make one parallelogram, the area of a trapezoid must be half of that, or (base 1 + base 2) * height / 2. Examples are provided to demonstrate calculating the area of trapezoids using this formula.

1. AREA OF TRAPEZIUM
Made by Jahnvi Tanwar

2. To find area of trapezium we will first
review
The Area of a Triangle & Parallelogram.
Then we are going to discover the
Area of a Trapezium.

3. Given the formula for
area of a rectangle, we are going to
use that information to discover the
formula for the area of a triangle.

4. Given a right triangle
Make a similar triangle and
flip it and put them both next
to each other.
What polygon is
this?
A Rectangle

5. We can use the formula for area of a rectangle
to find the formula for area of a triangle.
b
A=
2
hA=b h
Two triangles make
one rectangle.
We want to find half of
the area of the rectangle.
base
height
b
h
We divide 2 since we are
finding half of the area

6. base
height
h
This holds true for any triangle
b h
A=
2
Notice when we put two right triangles together it made
a rectangle. When we put two isosceles triangle
together it made a parallelogram. We are still finding
half the area so we divide by 2.

7. A triangle is half the area of a rectangle.
To find the area of a triangle, you use the
rectangle formula (base times height)
and divide it in half.
A = base •height
2
5 m
12 m
13 m
A = 5 • 12
2
= 30 m2
A=
1
2
bhbh
A=
2

8. Given the formula for
area of a triangle and the formula
for area of a parallelogram we are
going to use that information to
discover the formula for the
area of a trapezoid

9. This trapezoid is regular.
Regular Trapezoid
This trapezoid is an irregular trapezoid.
Irregular Trapezoid
Also known as an
Isosceles Trapezoid

10. b2
b1
h
Copy that trapezoid, flip it over,
and put it next to the original
b2
b1
h
Give the height, base 1 & base 2
(b1 + b2)
What polygon
is it now?
Parallelogram

11. Notice that the trapezium is half the area of the
parallelogram.
(b1 + b2)
h
Given our original trapezoidput together with a similar
flipped trapezoid, we found it made a parallelogram.
We are going to use the area of a parallelogram
to find the area of a trapezium.
It takes two trapezium to make
one parallelogram.

12. (b1 + b2)
h
Parallelogram Trapezoid
Notice that the trapezoid is half the area
of the parallelogram. How do we find
half the area?
2
A = (b1 + b2) * h
Hint: Think of
area of a triangle
A= b*h

13. Area of Trapezoid2 in
6 in
3 in
= 12
2
A = (b1 + b2) •h
A=(2+6)*3
2
=
(8)*3
2
=
24
2

14. 4
5
7
6
Here is another
way to look at the
trapezoid formula.
Instead of dividing
by 2, multiply by ½
A=1(b1 + b2)*h
2
A=1(5+7)*4
2
A=1(12)*4
2
A=6*4
=24

15. The End!