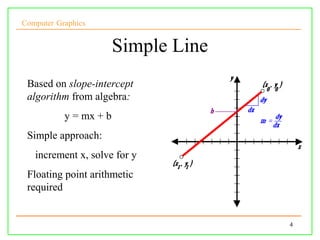
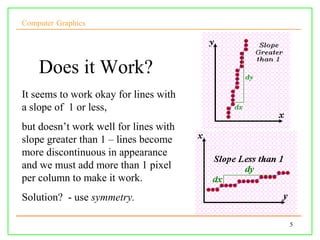
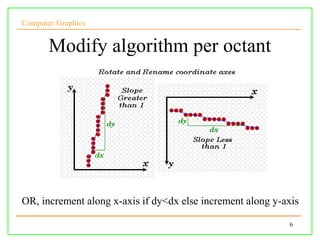
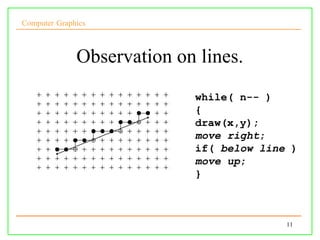
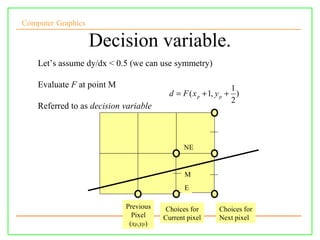
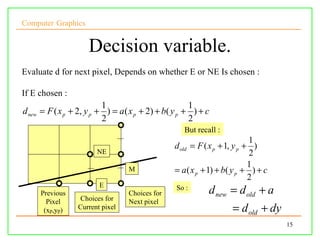
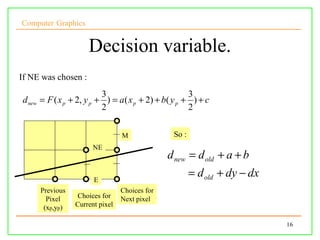
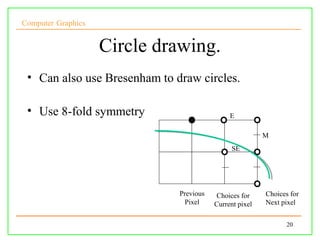
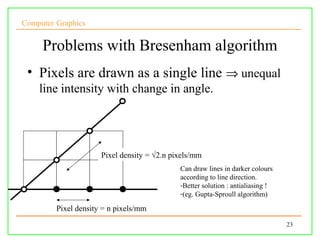
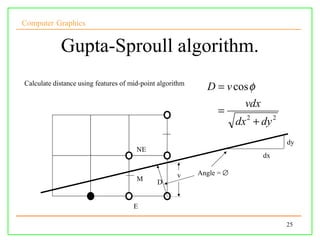
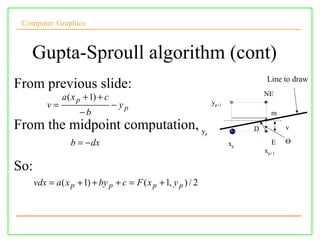
The document discusses algorithms for drawing lines and circles in computer graphics. It begins by explaining how lines must be approximated on a discrete pixel display. It then covers the slope-intercept algorithm, DDA algorithm, and Bresenham's midpoint algorithm for drawing lines using integer arithmetic. Finally, it discusses how the Gupta-Sproull algorithm improves on Bresenham by adding antialiasing through distance-based pixel coloring.

1. Computer Graphics
Computer Graphics
Lecture 3
Line & Circle Drawing

2. Computer Graphics
Towards the Ideal Line
• We can only do a discrete approximation
• Illuminate pixels as close to the true path as
possible, consider bi-level display only
– Pixels are either lit or not lit
2

3. Computer Graphics
What is an ideal line
• Must appear straight and continuous
– Only possible axis-aligned and 45o lines
• Must interpolate both defining end points
• Must have uniform density and intensity
– Consistent within a line and over all lines
– What about antialiasing?
• Must be efficient, drawn quickly
– Lots of them are required!!!
3

4. Computer Graphics
Simple Line
Based on slope-intercept
algorithm from algebra:
y = mx + b
Simple approach:
increment x, solve for y
Floating point arithmetic
required
4

5. Computer Graphics
Does it Work?
It seems to work okay for lines with
a slope of 1 or less,
but doesn’t work well for lines with
slope greater than 1 – lines become
more discontinuous in appearance
and we must add more than 1 pixel
per column to make it work.
Solution? - use symmetry.
5

6. Computer Graphics
Modify algorithm per octant
OR, increment along x-axis if dy<dx else increment along y-axis
6

7. Computer Graphics
DDA algorithm
• DDA = Digital Differential Analyser
– finite differences
• Treat line as parametric equation in t :
Start point - ( x1 , y1 ) x(t ) = x1 + t ( x2 − x1 )
End point - ( x2 , y2 )
y (t ) = y1 + t ( y2 − y1 )
7

8. Computer Graphics
DDA Algorithm x(t ) = x1 + t ( x2 − x1 )
y (t ) = y1 + t ( y2 − y1 )
dx
• Start at t = 0 xnew = xold +
dt
• At each step, increment t by dt ynew = yold +
dy
dt
• Choose appropriate value for dt dx = x2 − x1
• Ensure no pixels are missed: dy = y2 − y1
– Implies: dx and dy
<1 <1
dt dt
• Set dt to maximum of dx and dy
8

9. Computer Graphics
DDA algorithm
line(int x1, int y1, int x2, int y2)
{ n - range of t.
float x,y;
int dx = x2-x1, dy = y2-y1;
int n = max(abs(dx),abs(dy));
float dt = n, dxdt = dx/dt, dydt = dy/dt;
x = x1;
y = y1;
while( n-- ) {
point(round(x),round(y));
x += dxdt;
y += dydt;
}
}
9

10. Computer Graphics
DDA algorithm
• Still need a lot of floating point arithmetic.
– 2 ‘round’s and 2 adds per pixel.
• Is there a simpler way ?
• Can we use only integer arithmetic ?
– Easier to implement in hardware.
10

11. Computer Graphics
Observation on lines.
while( n-- )
{
draw(x,y);
move right;
if( below line )
move up;
}
11

12. Computer Graphics
Testing for the side of a line.
• Need a test to determine which side of a
line a pixel lies.
• Write the line in implicit form:
F ( x, y ) = ax + by + c = 0
•If (b<0) F<0 for points above the line, F>0 for
points below.
12

13. Computer Graphics
Testing for the side of a line.
F ( x, y ) = ax + by + c = 0
• Need to find coefficients a,b,c.
• Recall explicit, slope-intercept form :
dy
y = mx + b and so y = x+b
dx
• So:
F ( x, y ) = dy.x − dx. y + c = 0
13

14. Computer Graphics
Decision variable.
Let’s assume dy/dx < 0.5 (we can use symmetry)
Evaluate F at point M 1
d = F ( x p + 1, y p + )
2
Referred to as decision variable
NE
M
E
Previous Choices for Choices for
Pixel Current pixel Next pixel
(xp,yp)

15. Computer Graphics
Decision variable.
Evaluate d for next pixel, Depends on whether E or NE Is chosen :
If E chosen :
1 1
d new = F ( x p + 2, y p + ) = a ( x p + 2) + b( y p + ) + c
2 2
But recall :
1
d old = F ( x p + 1, y p + )
NE 2
1
M = a ( x p + 1) + b( y p + ) + c
2
E
Previous Choices for
So :
d new = d old + a
Pixel Choices for Next pixel
(xp,yp) Current pixel = d old + dy
15

16. Computer Graphics
Decision variable.
If NE was chosen :
3 3
d new = F ( x p + 2, y p + ) = a ( x p + 2) + b( y p + ) + c
2 2
M So :
NE
d new = d old + a + b
E
= d old + dy − dx
Previous Choices for
Pixel Choices for Next pixel
(xp,yp) Current pixel
16

17. Computer Graphics
Summary of mid-point algorithm
• Choose between 2 pixels at each step based
upon the sign of a decision variable.
• Update the decision variable based upon
which pixel is chosen.
• Start point is simply first endpoint (x1,y1).
• Need to calculate the initial value for d
17

18. Computer Graphics
Initial value of d.
Start point is (x1,y1)
1 1
d start = F ( x1 + 1, y1 + ) = a( x1 + 1) + b( y1 + ) + c
2 2
b
= ax1 + by1 + c + a +
2
b
= F ( x1 , y1 ) + a +
2
But (x1,y1) is a point on the line, so F(x1,y1) =0
d start = dy − dx / 2
Conventional to multiply by 2 to remove fraction ⇒ doesn’t effect sign.
18

19. Computer Graphics
Midpoint algorithm
void MidpointLine(int
x1,y1,x2,y2) while (x < x2) {
{ if (d<= 0) {
int dx=x2-x1; d+=incrE;
x++
int dy=y2-y1; } else {
int d=2*dy-dx; d+=incrNE;
x++;
int increE=2*dy; y++;
int incrNE=2*(dy-dx); }
WritePixel(x,y);
x=x1; }
y=y1; }
WritePixel(x,y);
19

20. Computer Graphics
Circle drawing.
• Can also use Bresenham to draw circles.
• Use 8-fold symmetry E
M
SE
Previous Choices for Choices for
Pixel Current pixel Next pixel
20

21. Computer Graphics
Circle drawing.
• Implicit form for a circle is:
f ( x, y ) = ( x − xc ) + ( y − yc ) − r
2 2 2
If SE is chosen d new = d old + (2 x p − 2 y p + 5)
If E is chosen d new = d old + (2 x p + 3)
• Functions are linear equations in terms of (xp,yp)
–Termed point of evaluation
21

22. Computer Graphics
Summary of line drawing so far.
• Explicit form of line
– Inefficient, difficult to control.
• Parametric form of line.
– Express line in terms of parameter t
– DDA algorithm
• Implicit form of line
– Only need to test for ‘side’ of line.
– Bresenham algorithm.
– Can also draw circles.
22

23. Computer Graphics
Problems with Bresenham algorithm
• Pixels are drawn as a single line ⇒ unequal
line intensity with change in angle.
Pixel density = √2.n pixels/mm
Can draw lines in darker colours
according to line direction.
-Better solution : antialiasing !
-(eg. Gupta-Sproull algorithm)
Pixel density = n pixels/mm
23

24. Computer Graphics
Gupta-Sproull algorithm.
• Calculate the distance of the line and the pixel
center
• Adjust the colour according to the distance

25. Computer Graphics
Gupta-Sproull algorithm.
Calculate distance using features of mid-point algorithm
D = v cos φ
vdx
=
dx 2 + dy 2
dy
NE
dx
v Angle = ∅
M D
E
25

26. Computer Graphics
Gupta-Sproull algorithm (cont)
Recall from the midpoint algorithm:
F ( x, y ) = 2( ax + by + c ) = 0 (doubled to avoid fraction) Line to draw
NE
yp+1
So y = ( ax + c ) m
−b D v
yp
xp E Θ
For pixel E: xp+1
x p +1 = x p + 1 y p +1 = y p v = y − y p +1
So:
a ( x p + 1) + c
v= − yp
−b

27. Computer Graphics
Gupta-Sproull algorithm (cont)
Line to draw
From previous slide:
NE
a ( x p + 1) + c
v= − yp yp+1
−b m
From the midpoint computation, y p
D v
b = − dx xp E Θ
xp+1
So:
vdx = a ( x p + 1) + by p + c = F ( x p + 1, y p ) / 2

28. Computer Graphics
Gupta-Sproull algorithm (cont)
From the midpoint algorithm, we had the decision
variable (remember?)
1
d = F ( M ) = F ( x p +1 , y p + )
2 Line to draw
Going back to our previous equation: NE
yp+1
2vdx = F ( x p + 1, y p ) m
= 2a ( x p + 1) + 2by p + 2c py D v
Θ
= 2a ( x p + 1) + 2b( y p + 1 / 2) − 2b / 2 + 2c xp E
xp+1
= F ( x p + 1, y p + 1 / 2) − b
= F (M ) − b
= d −b
= d + dx

29. Computer Graphics
Gupta-Sproull algorithm (cont)
So,
d + dx
D=
2 dx 2 + dy 2
And the denominator is constant
Since we are blurring the line, we also need to
compute the distances to points y p – 1 and yp + 1
numerator for y p − 1 ⇒ 2(1 − v)dx = 2dx − 2vdx
numerator for y p + 1 ⇒ 2(1 + v)dx = 2dx + 2vdx

30. Gupta-Sproull algorithm (cont)
Computer Graphics
If the NE pixel had been chosen:
2vdx = F ( x p + 1, y p + 1)
= 2a( x p + 1) + 2(by p + 1) + 2c
= 2a( x p + 1) + 2b( y p + 1 / 2) + 2b / 2 + 2c
= F ( x p + 1, y p + 1 / 2) + b
= F (M ) + b
= d +b
= d − dx
numerator for y p + 2 ⇒ 2(1 − v)dx = 2dx − 2vdx
numerator for y p ⇒ 2(1 + v)dx = 2dx + 2vdx

31. Computer Graphics
Gupta-Sproull algorithm (cont)
• Compute midpoint line algorithm, with the following alterations:
• At each iteration of the algorithm:
– If the E pixel is chosen, set numerator = d + dx
– If the NE pixel is chosen, set numerator = d – dx
– Update d as in the regular algorithm
– Compute D = numerator/denominator
– Color the current pixel according to D
– Compute Dupper = (2dx-2vdx)/denominator
– Compute Dlower = (2dx+2vdx)/denominator
– Color upper and lower accordingly