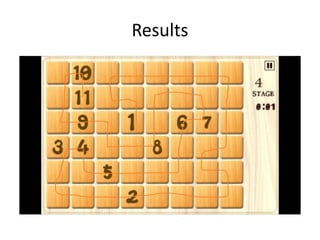
The document presents a model checking approach to solve a number-based puzzle game, outlining the requirements and encoding formulation using the NuSMV tool. Key elements include starting from the lowest number, covering each plate without revisiting, and ensuring the game sequence ends at the highest number within 47 transitions. The solution involves defining state transitions, marking plates as visited, and validating the goal state through logical specifications.

1. Model Checking For Puzzle Solving
By Anit Thapaliya
Software Engineering Lab
Department of Computer Science
Kyonggi University
Suwon, South Korea

2. Problem Background
A number based puzzle game where we
a. Must start at lowest number (1)
b. Must follow the sequence of number
c. Must cover all the plates
d. Finish at the higher number
Game Outline

3. Problem Formulation
Using Model Checking Tool
NuSMV
Consideration
1. Start from the lowest number
2. Follow sequence in order
3. Cover each plates
4. Finish at the highest number

4. Problem Formulation
Using Model Checking Tool
NuSMV
NuSMV requires the program to look for any solution whose number of transitions
is up to 47. Given my encoding of the problem, if no solution is found within 47
steps then we can safely conclude that there exists no possible solution for the input
table.
From our earlier solution it is clear to us that this is due to a rather poor encoding of
the problem (Our LTL property is overly complicated).

5. Problem Formulation
Using Model Checking Tool
NuSMV
•Modeling phase:
•Model the transition system under consideration
•Requirement 1: Visit every plates for which I consider a index of 0-47 for
identifying every available plates.
•Requirement 2: Follow the provided sequences for which I consider the
the given sequences in association with their relative indexing i.e. initial
lowest no 1 is in the index of 19.
•Requirement 3 : Avoid plates visiting twice for which I consider an array
of index 0-47 in Boolean form to represent whether the plates is visited
or not {0 for not visited & 1 for visited}
•Requiremt 4: Must start at lowest no and finish at highest no for which
our start point is the index having the lowest number and the end point is
the deadlock stage having the highest number.

6. Problem Solution
Using Model Checking Tool
NuSMV
MODULE main
VAR
index : 0..47; -- current position
sequence : {19, 43, 24, 25, 34, 21, 22, 28, 17, 1, 9};
plates : array 0..47 of { 0, 1 };
-- 0: plate not visited, 1: plate visited

7. Problem Solution
Our Goal: End Point
DEFINE
goal_state := sequence = 9 & index = 9 &
plates[0] = 1 & plates[1] = 1 & plates[2] = 1 & plates[3] = 1 &
plates[4] = 1 & plates[5] = 1 & plates[6] = 1 & plates[7] = 1 &
plates[8] = 1 & plates[9] = 1 & plates[10] = 1 & plates[11]=1 &
plates[12] = 1 & plates[13] = 1 & plates[14] = 1 & plates[15]= 1 &
plates[16] = 1 & plates[17] = 1 & plates[18] = 1 & plates[19]= 1 &
plates[20] = 1 & plates[21] = 1 & plates[22] = 1 & plates[23]= 1 &
plates[24] = 1 & plates[25] = 1 & plates[26] = 1 & plates[27]= 1 &
plates[28] = 1 & plates[29] = 1 & plates[30] = 1 & plates[31]= 1 &
plates[32] = 1 & plates[33] = 1 & plates[34] = 1 & plates[35]= 1 &
plates[36] = 1 & plates[37] = 1 & plates[38] = 1 & plates[39]= 1 &
plates[40] = 1 & plates[41] = 1 & plates[42] = 1 & plates[43]= 1 &
plates[44] = 1 & plates[45] = 1 & plates[46] = 1 & plates[47] = 1;

8. Problem Solution
ASSIGN
init(index) := 19;
init(sequence) := 19;
--initialize plate configuration
init(plates[0]) := 0;
init(plates[1]) := 0;
init(plates[2]) := 0;
init(plates[3]) := 0;
init(plates[4]) := 0;
…
init(plates[19]) := 1;
..
init(plates[47]) := 0;

9. Problem Solution
-- possible moves from any given plate, ignoring
-- the restriction over visiting the same plate
-- more than once
next(index) := case
index = 0 : {1, 8};
index = 1 : {0, 2, 9};
..
index = 8 : {0, 9, 16};
-- end plate: omitted (index 9: end plate)
index = 16 : {8, 17, 24};
index = 17 : {9, 16, 18, 25};
..
index = 47 : {39, 46};
TRUE : index;
esac;

10. Problem Solution
-- advance sequence only when we hit the correct plate on the table
next(sequence) := case
-- starting plate: omitted
sequence = 19 & next(index) = 43 : 43;
sequence = 43 & next(index) = 24 : 24;
sequence = 24 & next(index) = 25 : 25;
sequence = 25 & next(index) = 34 : 34;
sequence = 34 & next(index) = 21 : 21;
sequence = 21 & next(index) = 22 : 22;
sequence = 22 & next(index) = 28 : 28;
sequence = 28 & next(index) = 17 : 17;
sequence = 17 & next(index) = 1 : 1;
sequence = 1 & next(index) = 9 : 9;
TRUE : sequence;
esac;

11. Problem Solution
-- mark each plate as visited as soon as we move on it
next(plates[0]) := case next(index) =0 : 1; TRUE : plates[0]; esac;
next(plates[1]) := case next(index) =1 : 1; TRUE : plates[1]; esac;
next(plates[2]) := case next(index) =2 : 1; TRUE : plates[2]; esac;
next(plates[3]) := case next(index) =3 : 1; TRUE : plates[3]; esac;
next(plates[4]) := case next(index) =4 : 1; TRUE : plates[4]; esac;
next(plates[5]) := case next(index) =5 : 1; TRUE : plates[5]; esac;
next(plates[6]) := case next(index) =6 : 1; TRUE : plates[6]; esac;
next(plates[7]) := case next(index) =7 : 1; TRUE : plates[7]; esac;
next(plates[8]) := case next(index) =8 : 1; TRUE : plates[8]; esac;
next(plates[9]) := case next(index) =9 : 1; TRUE : plates[9]; esac;
…
next(plates[47]) := case next(index) =10 : 1; TRUE : plates[47]; esac;

12. Problem Solution
-- forbid stepping over an already visited plate,
-- unless it is the end plate
TRANS
(index = 9) | (plates[next(index)] != 1)
-- There is no possible path that reaches the goal state
LTLSPEC !(F goal_state)

13. Output

15. Results

16. Thank You