Downloaded 51 times
![アダブースト アルゴリズ
ム
・初期化 重み
・step1[ｆの決定]
T
回
繰
り ・step2[αの計算]
返
す
・step3[重み更
新]
・出
力](https://image.slidesharecdn.com/14-130304013828-phpapp02/85/14-14-320.jpg)
![Uブースト アルゴリズム
アダブーストとほぼいっしょ
・初期化
T
回 アダブースト
繰
り ・step2[αの計算]
返
す
・step4[重み更
新]
・出
力](https://image.slidesharecdn.com/14-130304013828-phpapp02/85/14-17-320.jpg)
![アダブーストM.1 アルゴリズム
・初期化
・step1[ｆの決定]
T
回
繰
り ・step2[αの計算]
返
す
・step3[重み更
新]
・出
力
！ポイント！ 重み付き誤り率＞0，5になることもある
重み付き誤り率≧0.5のときは使えない！
それなりに“強い”弱学習器でないとだめ・・・](https://image.slidesharecdn.com/14-130304013828-phpapp02/85/14-19-320.jpg)
![アダブーストM.2 アルゴリズム
True? or false?
弱学習器改め、 「弱仮
説」
・初期化
T
回
繰
り ・step2[αの計算]
返
す
・step4[重み更
新]
・出 やってることはいっしょ
より正確な判別器を選んで
力 不正解に敏感になるように重み更新](https://image.slidesharecdn.com/14-130304013828-phpapp02/85/14-21-320.jpg)
![バギング（adabag）
> library(kernlab)
> data(spam)
> set.seed(50)
> tr.num<-sample(4601,2500)
> spam.train<-spam[tr.num,]
> spam.test<-spam[-tr.num,]
> library(adabag)
> spam.bag<-bagging(type~.,data=spam.train)
> spam.predict<-predict(spam.bag,spam.test)
> 1-spam.predict$error
[1] 0.9057592
予測誤差 正判別率％](https://image.slidesharecdn.com/14-130304013828-phpapp02/85/14-27-320.jpg)
![アダブースト（adabag）
> library(rpart)
> library(adabag)
> data <- iris
> ndata <- nrow(data)
> set.seed(101)
> ridx <- sample(ndata, ndata * 0.5)
> data.train <- data[ridx,]
> data.test <- data[-ridx,]
> data.adaCv <- boosting(Species ~ .,data
= data.train, mfinal = 10)
> resultPredict <- predict(data.adaCv,
newdata = data.test, type="class")
> resultPredict](https://image.slidesharecdn.com/14-130304013828-phpapp02/85/14-28-320.jpg)
![$confusion
Observed Class
Predicted Class setosa versicolor virginica
setosa 26 0 0
versicolor 0 17 3
virginica 0 1 28
$error
[1] 0.05333333
予測誤差：５％](https://image.slidesharecdn.com/14-130304013828-phpapp02/85/14-29-320.jpg)
![[DL輪読会]Deep Learning 第5章 機械学習の基礎](https://cdn.slidesharecdn.com/ss_thumbnails/deeplearning5-180601021956-thumbnail.jpg?width=640&height=640&fit=bounds)
第14章集団学習
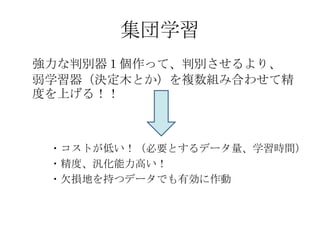
- 1. Rで学ぶデータサイエンス パターン認識 第14章 集団学習 降旗啓
- 2.
- 3. 他手法との比較 ちなみにこれは 「Random Forest」 集団学習一種 今回は割愛。
- 4. （まずは）2値判別アルゴリズム バギング （bagging） ブースティング (boosting)
- 5. （まずは）2値判別アルゴリズム バギング （bagging） ブースティング (boosting)
- 6. バギング Bootstrap AGGregatING ブートストラップで弱学習器を集めるアルゴ ブートストラップ法(ノンパラメトリッ リズム ク版) ブートストラップ小さな標本から得られた 母数の推定値の誤差を推定することが可能 母集団 になり，その精度を調べることができ る！！ ランダム サンプリン グ 標本 標本を擬似母集団と考えて リサンプリング B回（適当に定める）復元抽出を行 う そこから ブ ブートストラップ推定量を求める ー ト 本ス ラ ッ プ 標
- 7. バギング 標本 リサンプリング ブ ー ト 本ス ラ ッ プ 標 判別問題・・・多数決 回帰問題・・・平均 (各弱学習器に標本をぶちこんで,各サンプルに (各弱学習器に標本をぶちこんで,各サンプルに つ ついて出力されたラベルを平均する) いて もっとも多いラベルを正しいラベルと みなす)
- 8. バギング んで、どのくらい優秀になった？ つまりバギング後、 弱学習器平均の標本推定値とのばらつき の 分だけ 誤差尐ない！
- 9. バギング バギングの特徴 • 過学習を起こしやすかったり、局所解に 陥りやすいものほど効果高い（出力の平 均化） • ブースティングと違って、弱学習器が事 例を重み付け出来なくても適用でき容易 • それぞれの学習器が独立（並列に実行 可） ➝貧弱な学習器の強化には向かない。 （ex. 天気予報50%であてるモデルを いくら
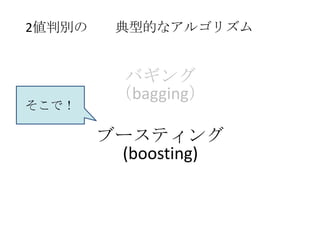
- 10. 2値判別の 典型的なアルゴリズム バギング （bagging） そこで！ ブースティング (boosting)
- 11. ブースティン グ ブースティング • 各試行を独立じゃなくする • 弱学習器を追加する際、逐次的に学習さ せる。 • 並列化が困難 ２値判別・・・アダブースト、Uブース ト 多値判別・・・アダブーストM1、 アダブーストM2
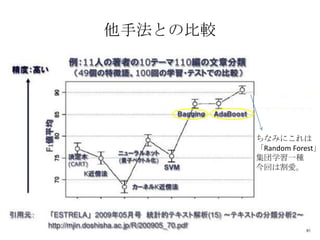
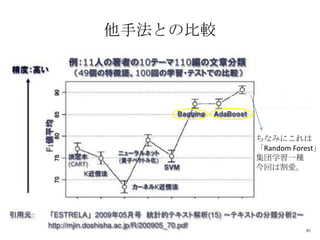
- 12. 他手法との比較 ちなみにこれは 「Random Forest」 集団学習一種 今回は割愛。
- 13. ブースティン グ アダブースト・Uブースト のイ メージ 間違ったものに敏感になる弱学習器を作ってく
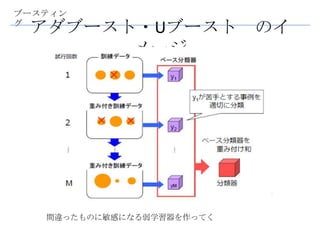
- 14. アダブースト アルゴリズ ム ・初期化 重み ・step1[ｆの決定] T 回 繰 り ・step2[αの計算] 返 す ・step3[重み更 新] ・出 力
- 16. Uブースト ・アダブーストを一般化したもの ・U関数を導入しロス関数を逐次的最小化 （Uは凸な単調増加関数） アダブーストと等価 ロジットブーストと等価 3.マダブースト 4.イーターブースト
- 17. Uブースト アルゴリズム アダブーストとほぼいっしょ ・初期化 T 回 アダブースト 繰 り ・step2[αの計算] 返 す ・step4[重み更 新] ・出 力
- 18. 2値から多値へ • アダブースト、Uブーストは2値で定義し てた • アダブーストM.1、アダブーストM.2とい う は多値で定義したアルゴリズム • M.1はアダブーストを2値からG値にしただ
- 19. アダブーストM.1 アルゴリズム ・初期化 ・step1[ｆの決定] T 回 繰 り ・step2[αの計算] 返 す ・step3[重み更 新] ・出 力 ！ポイント！ 重み付き誤り率＞0，5になることもある 重み付き誤り率≧0.5のときは使えない！ それなりに“強い”弱学習器でないとだめ・・・
- 20. M.1 微妙・・・ ex.晴れ、雨、雪の3ラベルの場合 2値だったら,「晴れ40％」の弱い学習器が「雨60%」の弱学習器とでき た。 しかし！3値になった瞬間、「晴れ40％」は依然弱いまま・・・ でも要求は重み付き誤り率0.5より小・・・ 1つ1つの判別器を多尐ゆとりをもたせて考慮. クラス集合に収まる？収まらない？として,2値判別として考える. M.２ どや！ ex.晴れ、雨、雪の3ラベルの場合 「晴れ」「晴れ以外」,「雨」「雨以外」,「雪」「雪以外」と考えれ ば 2値で考えられる！
- 21. アダブーストM.2 アルゴリズム True? or false? 弱学習器改め、 「弱仮 説」 ・初期化 T 回 繰 り ・step2[αの計算] 返 す ・step4[重み更 新] ・出 やってることはいっしょ より正確な判別器を選んで 力 不正解に敏感になるように重み更新
- 22.
- 23. パッケージ ○バギング ・adabag ・ipred ○ブースティング ・ada ・adabag ○ランダムフォレスト ・randomForest
- 24. Adabagパッケージ • バギングとブースティングが実装されて る • 弱学習器として決定木（rpartパッケー ジ） • 関数 ・bagging ・boosting
- 25.
- 26.
- 27. バギング（adabag） > library(kernlab) > data(spam) >set.seed(50) > tr.num<-sample(4601,2500) > spam.train<-spam[tr.num,] > spam.test<-spam[-tr.num,] > library(adabag) > spam.bag<-bagging(type~.,data=spam.train) > spam.predict<-predict(spam.bag,spam.test) > 1-spam.predict$error [1] 0.9057592 予測誤差 正判別率％
- 28. アダブースト（adabag） > library(rpart) > library(adabag) >data <- iris > ndata <- nrow(data) > set.seed(101) > ridx <- sample(ndata, ndata * 0.5) > data.train <- data[ridx,] > data.test <- data[-ridx,] > data.adaCv <- boosting(Species ~ .,data = data.train, mfinal = 10) > resultPredict <- predict(data.adaCv, newdata = data.test, type="class") > resultPredict
- 29. $confusion Observed Class Predicted Classsetosa versicolor virginica setosa 26 0 0 versicolor 0 17 3 virginica 0 1 28 $error [1] 0.05333333 予測誤差：５％