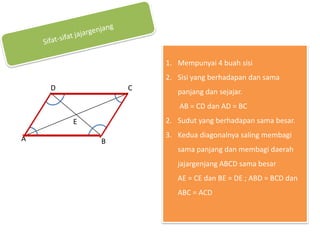
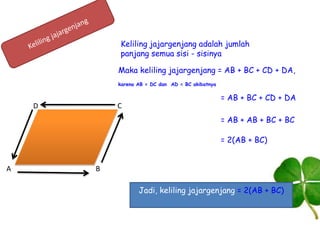
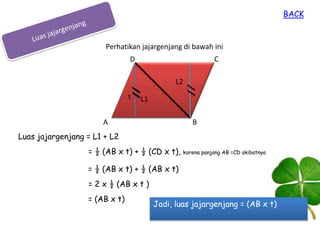
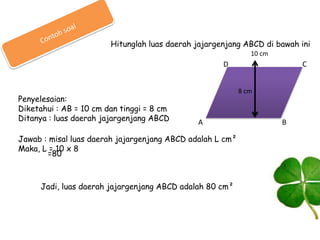
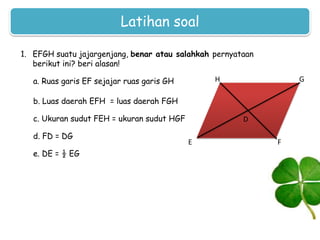
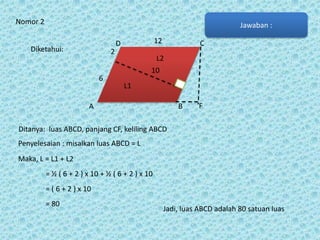
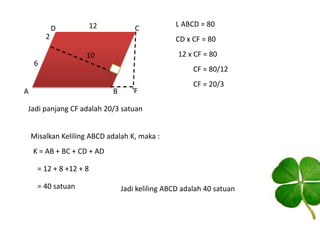
Dokumen ini membahas tentang jajargenjang, termasuk pengertian, sifat-sifat, dan cara menghitung keliling serta luasnya. Jajargenjang didefinisikan sebagai bangun datar dengan 4 sisi yang saling berhadapan sama panjang dan sejajar, di mana kelilingnya adalah 2(ab + bc) dan luasnya adalah ab x t. Terdapat juga latihan soal yang berkaitan dengan jajargenjang untuk meningkatkan pemahaman siswa.

1. JAJARGENJANG
Disusun oleh:
Mia Sari Hanty Ritonga (1000639)

2. Sasaran
Siswa SMP kelas VII
semester 2 (genap)

4. Kompetensi Dasar
Memahami pengertian dan sifat-sifat serta menghitung keliling
dan luas bangun segiempat dan menggunakannya dalam
pemecahan masalah
Indikator
1. Memahami
pengertian
dan
sifat-sifat
Jajargenjang.
2. Menyelesaikan masalah yang berkaitan dengan
menghitung
keliling
dan
luas
bangun
Jajargenjang.
BACK

5. Gambar 1
Gambar 3
Gambar 2
Gambar 1
Manakah di antara
benda-benda di atas
yang permukaannya
berbentuk jajargenjang?

6. 1. Mempunyai 4 buah sisi
2. Sisi yang berhadapan dan sama
D
C
panjang dan sejajar.
AB = CD dan AD = BC
2. Sudut yang berhadapan sama besar.
E
A
B
3. Kedua diagonalnya saling membagi
sama panjang dan membagi daerah
jajargenjang ABCD sama besar
AE = CE dan BE = DE ; ABD = BCD dan
ABC = ACD

7. Jadi, apa itu
jajargenjang?
Jajargenjang adalah bangun datar yang
dibatasi oleh 4 buah sisi dengan sisi-sisi
yang saling berhadapan sama panjang dan
sejajar, dan sisi-sisi yang bersebelahan
tidak saling tegak lurus.

8. Keliling jajargenjang adalah jumlah
panjang semua sisi - sisinya
Maka keliling jajargenjang = AB + BC + CD + DA,
karena AB = DC dan AD = BC akibatnya
C
D
= AB + BC + CD + DA
= AB + AB + BC + BC
= 2(AB + BC)
A
B
Jadi, keliling jajargenjang = 2(AB + BC)

9. BACK
Perhatikan jajargenjang di bawah ini
C
D
L2
t
L1
A
B
Luas jajargenjang = L1 + L2
= ½ (AB x t) + ½ (CD x t),
karena panjang AB =CD akibatnya
= ½ (AB x t) + ½ (AB x t)
= 2 x ½ (AB x t )
= (AB x t)
Jadi, luas jajargenjang = (AB x t)

10. Hitunglah luas daerah jajargenjang ABCD di bawah ini
10 cm
C
D
Penyelesaian:
Diketahui : AB = 10 cm dan tinggi = 8 cm
Ditanya : luas daerah jajargenjang ABCD
8 cm
A
Jawab : misal luas daerah jajargenjang ABCD adalah L cm²
Maka, L = 10 x 8
=80
Jadi, luas daerah jajargenjang ABCD adalah 80 cm²
B

11. Latihan soal
1. EFGH suatu jajargenjang, benar atau salahkah pernyataan
berikut ini? beri alasan!
a. Ruas garis EF sejajar ruas garis GH
G
H
b. Luas daerah EFH = luas daerah FGH
c. Ukuran sudut FEH = ukuran sudut HGF
d. FD = DG
e. DE = ½ EG
D
E
F

12. Latihan soal
2. Jika ABCD suatu jajargenjang seperti tampak pada gambar
berikut ini, maka hitunglah luas ABCD, panjang ruas garis CF dan
keliling ABCD!
D
12
C
2
6
A
10
B
F

13. Jawaban :
Nomor 1
a.
Benar, menurut sifat-sifat jajargenjang, sisi yang berhadapan sama besar dan
sejajar. Karena sisi EF berhadapan dengan sisi GH maka ruas garis EF sejajar ruas
garis GH
b.
Benar, menurut sifat-sifat jajargenjang, dua derah yang dibagi oleh diagonal
jajargenjang akan mempunyai luas daerah yang sama. Karena EFH dan FGH
merupakan daerah yang dibagi oleh salah satu diagonal jajargenjang maka EFH dan
FGH memiliki luas daerah yang sama
c.
benar, menurut sifat-sifat jajargenjang, dua sudut yang berhadapan akan memiliki
ukuran yang sama. Karena sudut FEH dan sudut FGH saling berhadapan maka
ukuran sudutnya sama
d.
Salah
e.
Benar, menurut sifat-sifat jajargenjang, kedua diagonalnya membagi dua bagian
sama panjang. Karena EG dibagi oleh FH di D maka panjang ED = ½ EG

14. Nomor 2
Jawaban :
12
D
Diketahui:
2
6
C
L2
10
L1
A
B
F
Ditanya: luas ABCD, panjang CF, keliling ABCD
Penyelesaian : misalkan luas ABCD = L
Maka, L = L1 + L2
= ½ ( 6 + 2 ) x 10 + ½ ( 6 + 2 ) x 10
= ( 6 + 2 ) x 10
= 80
Jadi, luas ABCD adalah 80 satuan luas

15. 12
D
C
2
6
L ABCD = 80
CD x CF = 80
12 x CF = 80
10
A
CF = 80/12
B
F
CF = 20/3
Jadi panjang CF adalah 20/3 satuan
Misalkan Keliling ABCD adalah K, maka :
K = AB + BC + CD + AD
= 12 + 8 +12 + 8
= 40 satuan
Jadi keliling ABCD adalah 40 satuan