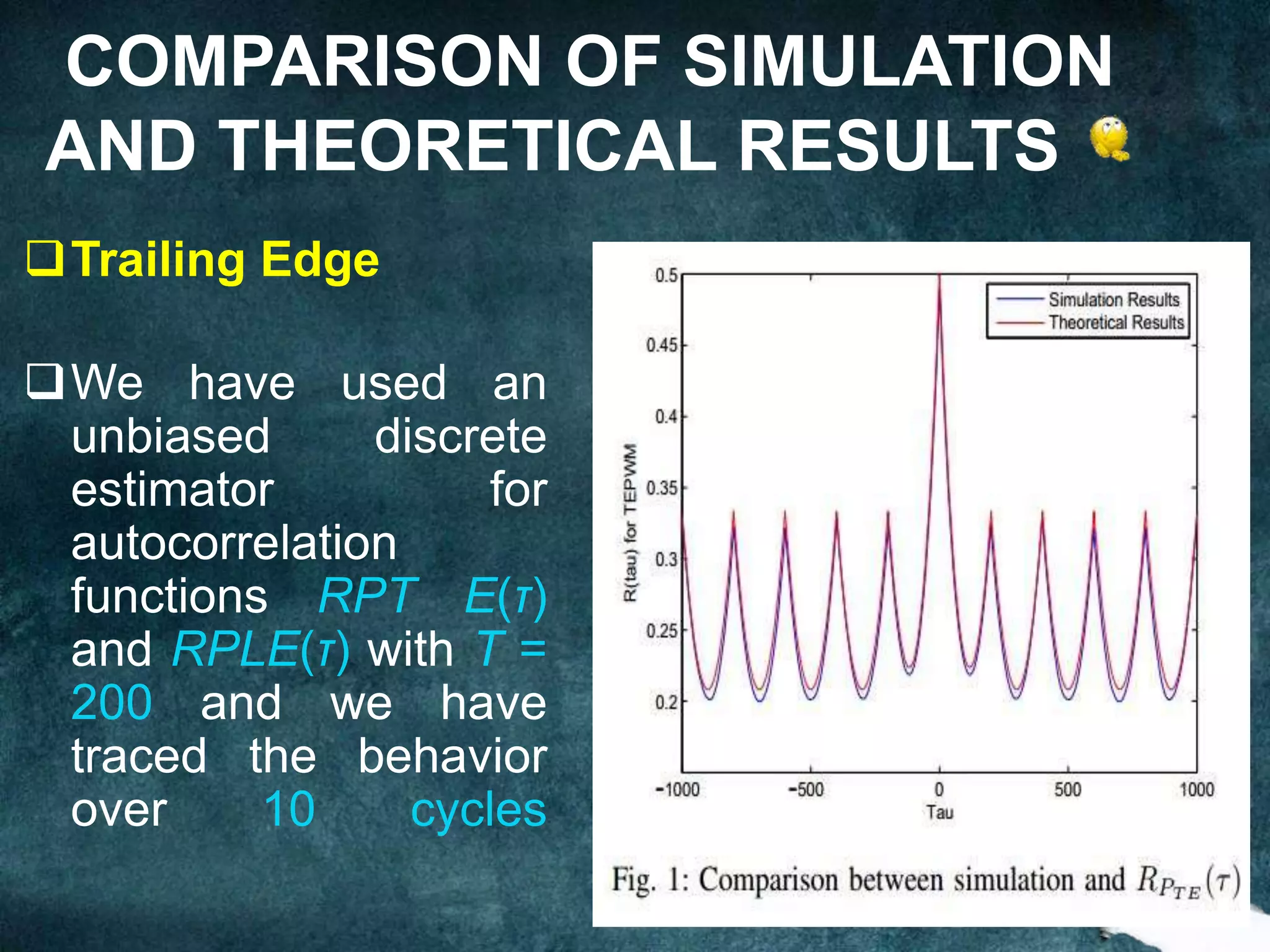
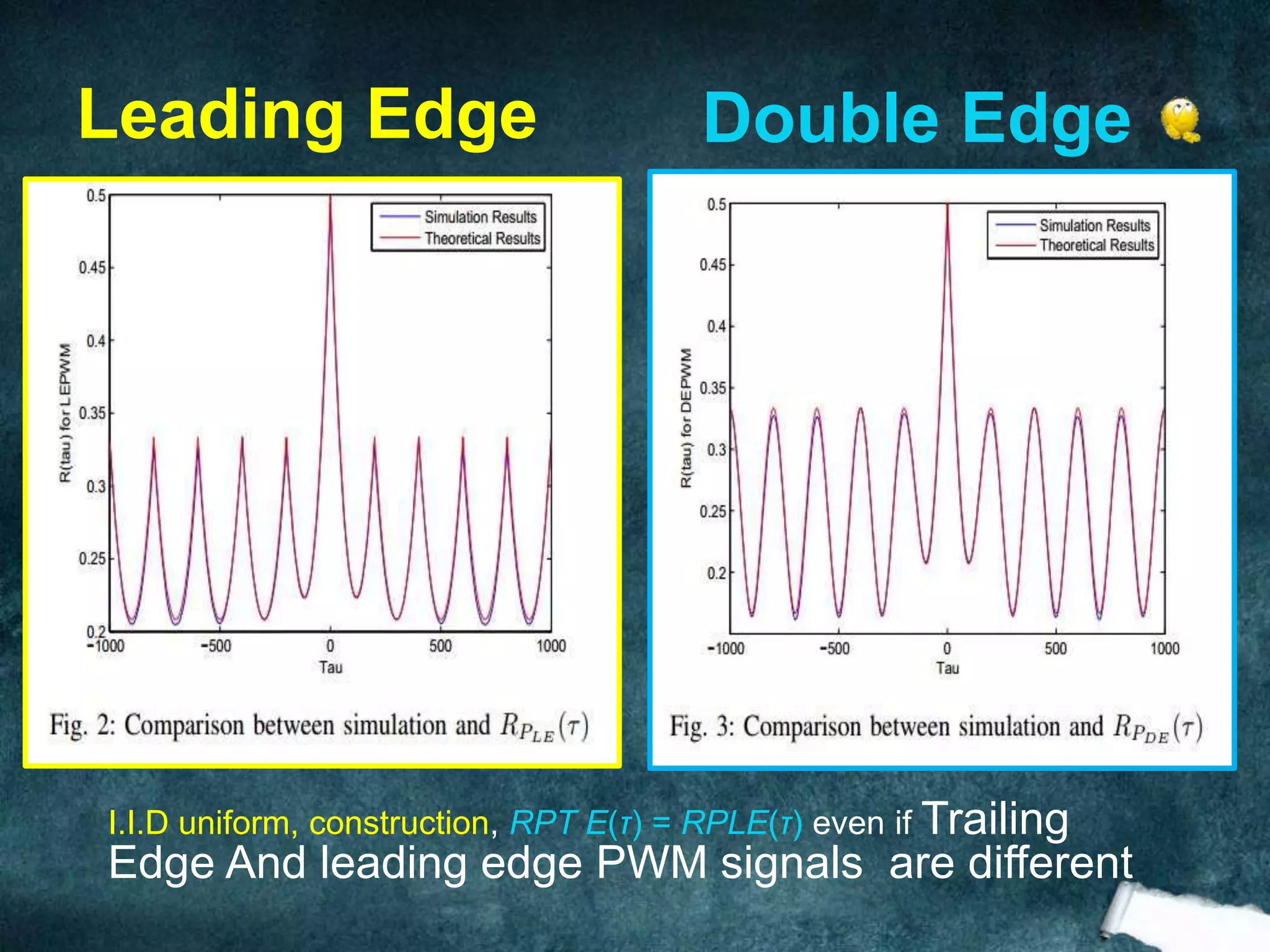
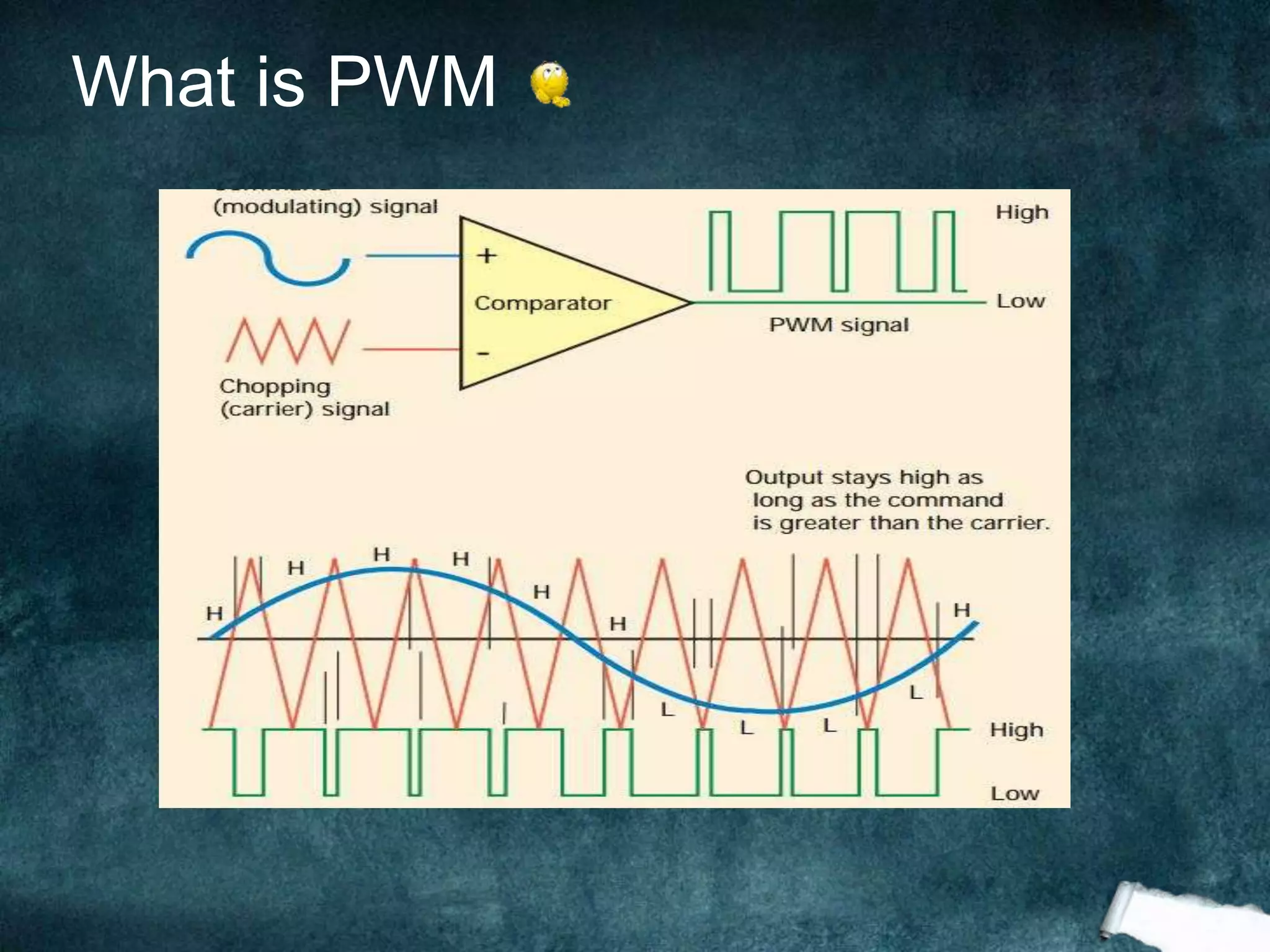
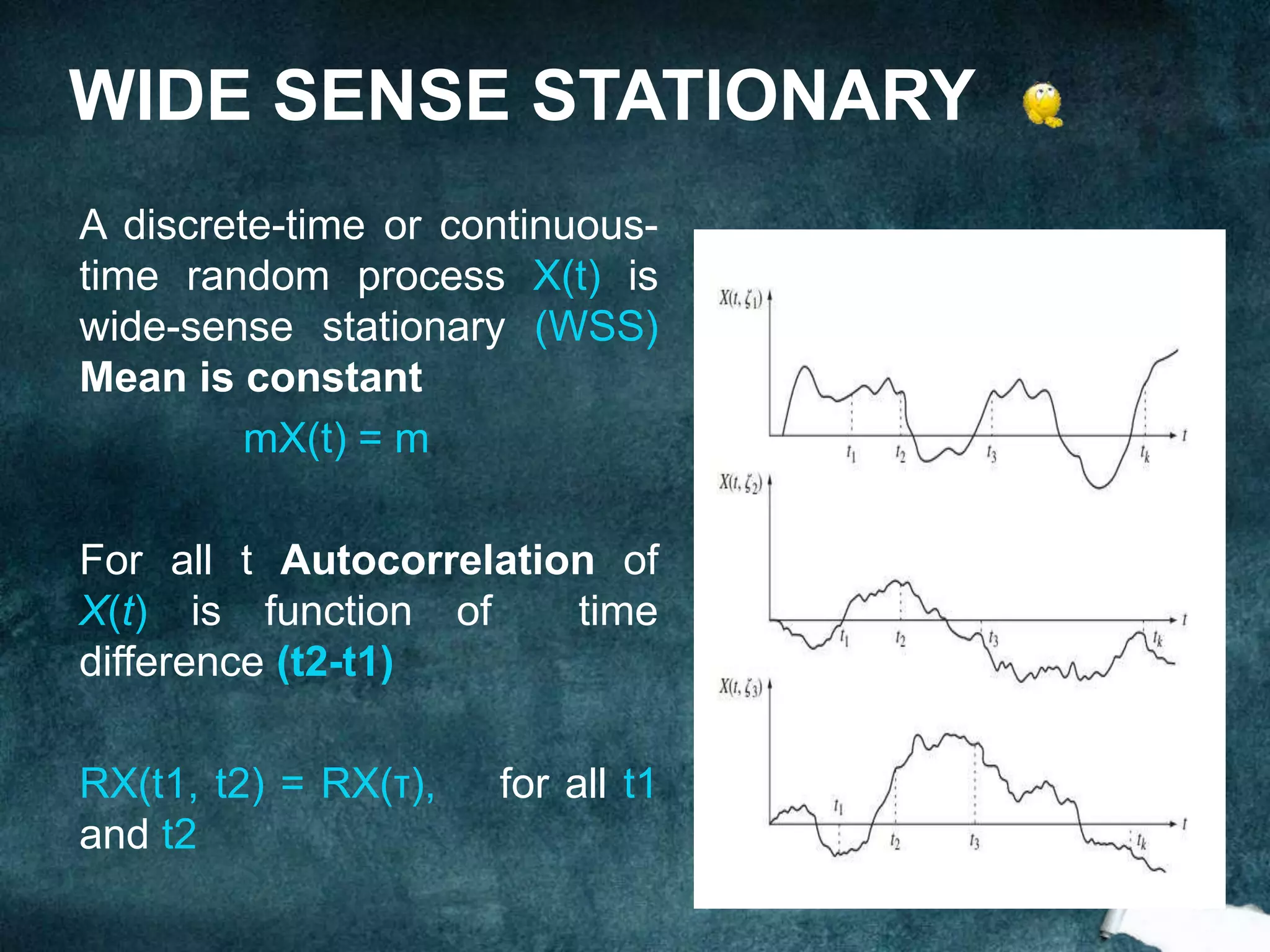
The document presents an analysis of pulse width modulation (PWM) signals, focusing on their stochastic characteristics, including mean, autocorrelation, and power spectral density (PSD). It discusses the conversion of non-stationary PWM signals into wide sense stationary (WSS) signals through different sampling techniques and presents simulation results compared with theoretical expectations. The findings indicate that PWM signals with randomized starting points and independent and identically distributed (i.i.d.) pulse widths are necessarily WSS.

2. Title:
IID STOCHASTIC ANALYSIS
OF PWM SIGNALS
GROUP MEMBERS:
AMER AZIZ 172203
SALMAN BASHIR 171228

3. CONTENTS
 To evaluate the basic stochastic characteristics
o Mean and Autocorrelation of PWM signals
o Power Spectral Density (PSD)
 Conversion of non stationary PWM signals into
simple wide sense stationary using different
sampling techniques
 For I.I.D uniformly distributed, the proposed
autocorrelation functions are tested with simulation

4. Beginning
INTRODUCTION
1
Presenter: Muhammad Salman Bashir

5. INTRODUCTION
 PWM (PULSE WIDTH MODULATION)
 Sampling methodology of input signal
 Types of PWM depending
 Make PWM signal wised sense stationary (WSS)
 Evaluation of stochastic characteristics namely
autocorrelation (ACF) and power spectral density (PSD)
theoretically
 Simulation of autocorrelation (ACF) for PWM signal
 Comparison of theoretically and simulation results
 Conclusion

6. Non Stationary
Randomize
Stating
point
Wide Sense
Stationary
How Work Flow
Mean and
auto
correlation
Simulation

7. What is PWM

8.  Trailing Edge PWM
Lead edge of trigger signal is
modulated.
 Leading Edge PWM
Trail edge of trigger signal is
modulated.
 Double Edge PWM
Pulse center is fixed and both
edges are modulated.
Types of PWM

9. Trailing Edge PWM
Mean of TEPWM
Leading Edge PWM
Mean of LEPWM
Double Edge PWM
Mean of DEPWM
NON STATIONARY PWM Signal
with fixed starting point

10. Presenter: Amer Aziz

11. A discrete-time or continuous-
time random process X(t) is
wide-sense stationary (WSS)
Mean is constant
mX(t) = m
For all t Autocorrelation of
X(t) is function of time
difference (t2-t1)
RX(t1, t2) = RX(τ), for all t1
and t2
WIDE SENSE STATIONARY

12.  Randomizing starting point
by Φ, uniformly distributed
over [0,T]
 Limiting input signal
amplitude(bk) over sample
interval [0,1] uniformly and
using sampling methodology
WSS and IID PWM signal
 Trailing Edge PMW Mean is
constant Autocorrelation is
function of difference as
τ=t-s
CONVERSION IN WIDE SENSE
STATIONARY

13. Leading Edge PWM
Mean is constant
Autocorrelation is function of
time difference

14. Double Edge PWM
Mean is constant
Autocorrelation is function
of time difference
We can also find PSD of
PWM signals.

15. Trailing Edge
COMPARISON OF SIMULATION
AND THEORETICAL RESULTS
We have used an
unbiased discrete
estimator for
autocorrelation
functions RPT E(τ)
and RPLE(τ) with T =
200 and we have
traced the behavior
over 10 cycles

16. I.I.D uniform, construction, RPT E(τ) = RPLE(τ) even if Trailing
Edge And leading edge PWM signals are different
Leading Edge Double Edge

17.  PWM signal with a fixed starting point is not necessarily
wide sense stationary
 PWM signal with randomized starting point and I.I.D pulse
widths over a symbol interval is necessarily WSS
 Using the autocorrelation functions, derived the power
spectrum densities (PSD) easily
 For I.I.D. uniform distribution case, we have shown the
accuracy of our results with simulations.
CONCLUSION