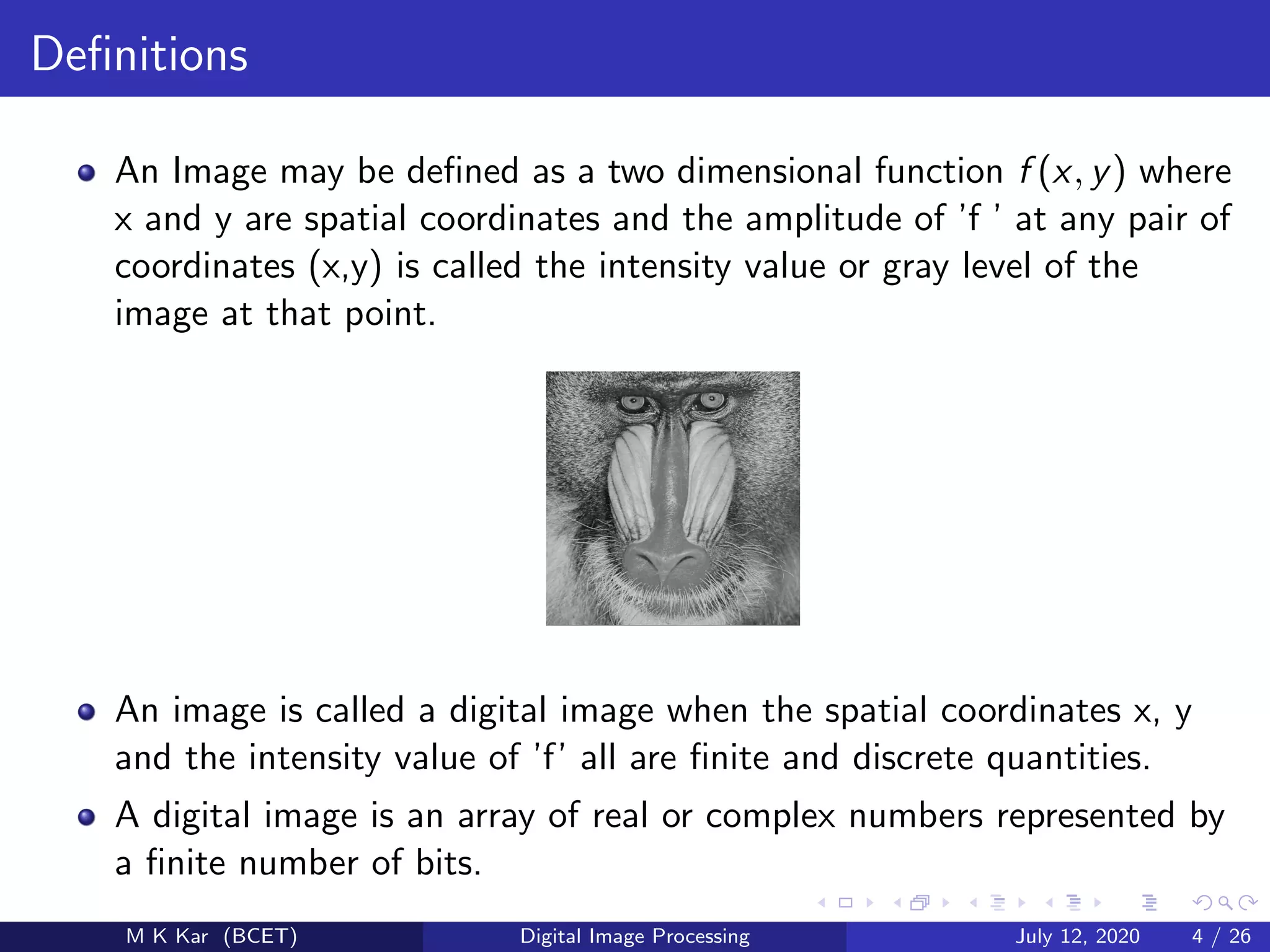
The document discusses digital image processing and is presented by M K Kar of Balasore College of Engineering and Technology. It covers fundamentals of digital image processing including representation of digital images, intensity transformations, spatial filtering, frequency domain representation, and applications in medicine, agriculture, industry and more. Transformation techniques like contrast stretching and histogram equalization are described. Spatial filters like averaging, median and Laplacian filters are covered along with sharpening and smoothing effects.

1. Digital Image Processing
M K Kar
Balasore college of Engineering and Technology
July 12, 2020
M K Kar (BCET) Digital Image Processing July 12, 2020 1 / 26

2. Overview
1 Fundamentals of Digital Image Processing
2 Representation of digital image
3 Intensity Transformation
4 Relation between pixels
5 Image Histogram
6 Fundamentals of Spatial Filtering
7 Frequency domain representation
M K Kar (BCET) Digital Image Processing July 12, 2020 2 / 26

3. Fundamentals of Digital Image Processing
Image processing involves changing the nature of an image in order to
either
improve its pictorial information for human interpretation.
render it more suitable for autonomous machine perception.
M K Kar (BCET) Digital Image Processing July 12, 2020 3 / 26

4. Definitions
An Image may be defined as a two dimensional function f (x, y) where
x and y are spatial coordinates and the amplitude of ’f ’ at any pair of
coordinates (x,y) is called the intensity value or gray level of the
image at that point.
An image is called a digital image when the spatial coordinates x, y
and the intensity value of ’f’ all are finite and discrete quantities.
A digital image is an array of real or complex numbers represented by
a finite number of bits.
M K Kar (BCET) Digital Image Processing July 12, 2020 4 / 26

5. Representation of digital image
A digital image is formed by sampling and quantization containing M
rows and N columns.
f (x, y) =





f (0, 0) f (0, 1) . . . f (0, N − 1)
f (1, 0)
...
f (1, 1) · · ·
...
f (1, N − 1)
...
f (M − 1, 0) f (M − 1, 0) · · · f (M − 1, N − 1)





Each element of this matrix is called an image element or picture
element or pixels.
The origin of a digital image is at the top left with the + x axis
extending downward and the + y axis extending to the right.
M K Kar (BCET) Digital Image Processing July 12, 2020 5 / 26

6. Representation of digital image
M K Kar (BCET) Digital Image Processing July 12, 2020 6 / 26

7. Types of digital image
An Image may be classified in to three types
Color Image
Grey Image
Binary Image
M K Kar (BCET) Digital Image Processing July 12, 2020 7 / 26

8. Application
Medicine
Agriculture
Industry
Law enforcement
Entertainment
Weatherforecast
M K Kar (BCET) Digital Image Processing July 12, 2020 8 / 26

9. Application
M K Kar (BCET) Digital Image Processing July 12, 2020 9 / 26

10. Intensity Transformations
The spatial domain processes can be denoted by the expression
g(x, y) = T[f (x, y)]
where f (x, y) is the input image and g(x, y) is the output image
M K Kar (BCET) Digital Image Processing July 12, 2020 10 / 26

11. Image Negatives
The negative of an image with intensity levels in the range [0, L − 1]
is obtained by using the negative transformation, given by the
expression s = (L − 1) − r.
Figure: image negetive
M K Kar (BCET) Digital Image Processing July 12, 2020 11 / 26

12. Log Transformations
The general form of log transformation is given by
s = c log(1 + r)
The general form of power law (gamma)transformation is given by
s = crγ
M K Kar (BCET) Digital Image Processing July 12, 2020 12 / 26

13. Contrast stretching
Contrast stretching is a process that expands the range of intensity
levels in an image so that it spans the full intensity range of the
recording medium or display device.
The result of contrast stretching is obtained by setting
(r1, s1) = (rmin, 0)
and
(r2, s2) = (rmax, L − 1)
where rmin and rmaxdenote the minimum and maximum intensity
levels in the image respectively.
M K Kar (BCET) Digital Image Processing July 12, 2020 13 / 26

14. Contrast stretching
Figure: Original image, Contrast image
M K Kar (BCET) Digital Image Processing July 12, 2020 14 / 26

15. Image Histogram
The histogram of a digital image with intensity levels in the range
[0,L-1] is a discrete function h(rk) = nk, where rk is the kth intensity
value and nkis the number of pixels in the image with intensity rk.
M K Kar (BCET) Digital Image Processing July 12, 2020 15 / 26

16. Histogram Equalization
The histogram equalization of a digital image with intensity levels in
the range [0, L − 1] is a discrete function sk = T(rk), where rk is the
kth intensity value and nkis the number of pixels in the image with
intensity rk is.
sk = T(rk) = (L − 1)
k
j=0
pr (rj ) =
(L − 1)
MN
k
j=0
(nj )
M K Kar (BCET) Digital Image Processing July 12, 2020 16 / 26

17. Histogram Equalization
0
1000
2000
3000
0 100 200
0
2000
4000
0 100 200
M K Kar (BCET) Digital Image Processing July 12, 2020 17 / 26

18. Fundamentals of Spatial Filtering
The spatial filter consist of a neighborhood and a predefined
operation that is performed on the image pixels encompassed by the
neighborhood.Filtering creates a new pixel with coordinates equal to
the coordinates of the center of the neighborhood and whose value is
the result of the filtering operation.
M K Kar (BCET) Digital Image Processing July 12, 2020 18 / 26

19. Image smoothing using Averaging/Box filter
Replacing the value of every pixel in an image by the average of the
intensity levels in the neighborhood defined by the filter mask, which
results in an image with reduced sharp transitions.
M K Kar (BCET) Digital Image Processing July 12, 2020 19 / 26

20. Image smoothing using Median filter
Median filter replaces the value of a pixel by the median of the
intensity values in the neighborhood of that pixel including the
original value of that pixel.
M K Kar (BCET) Digital Image Processing July 12, 2020 20 / 26

21. Image sharpening using Laplacian
Laplacian is the simplest isotropic derivative operator(rotation
invarient) which is defined for an image function f (x, y) is given by
2
f =
∂2f
∂x2
+
∂2f
∂y2
.
For any image pixel f (x, y) , the laplacian is given by
2
f (x, y) = f (x+1, y)+f (x−1, y)+f (x, y +1)+f (x, y −1)−4f (x, y)
This equation can be implemented using the filter mask given below


0 1 0
1 −4 1
0 1 0


or 

0 −1 0
−1 4 −1
0 −1 0


M K Kar (BCET) Digital Image Processing July 12, 2020 21 / 26

22. Image sharpening using Laplacian
Figure: Sharpened Image and Laplacian Image.
Figure: Laplacian Image and Sharpened Image.
M K Kar (BCET) Digital Image Processing July 12, 2020 22 / 26

23. Image Representation in frequency Domain
A fourier transform is used to transform an intensity image in to the
domain of spatial frequency using the 2D-DFT.
F(u, v) =
M−1
x=0
N−1
y=0
f (x, y)e
−j2πux
M e
−j2πvy
N
M K Kar (BCET) Digital Image Processing July 12, 2020 23 / 26

24. Image Representation in frequency Domain
Figure: Fourier transformed Image and spectral Image.
M K Kar (BCET) Digital Image Processing July 12, 2020 24 / 26

25. References
Rafael C. Gonzalez, Richard E. Woods (2008)
Digital Image Processing
Pearson Education 2009,Third Edition.
M K Kar (BCET) Digital Image Processing July 12, 2020 25 / 26

26. The End
M K Kar (BCET) Digital Image Processing July 12, 2020 26 / 26