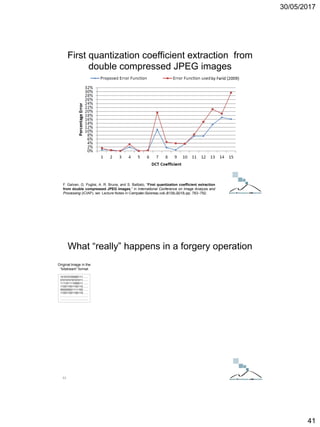
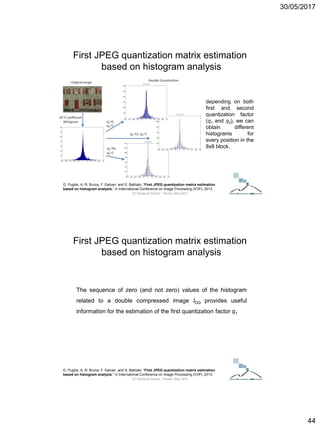
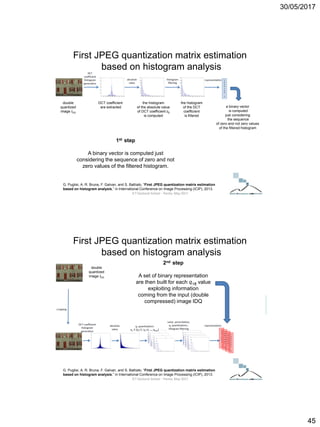
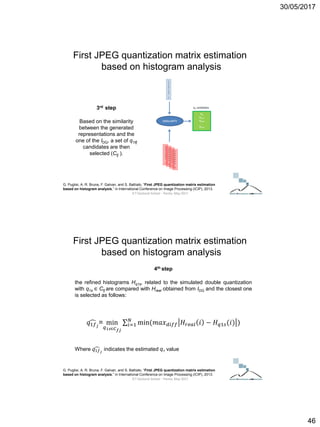
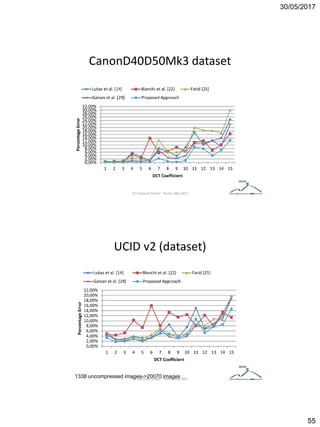
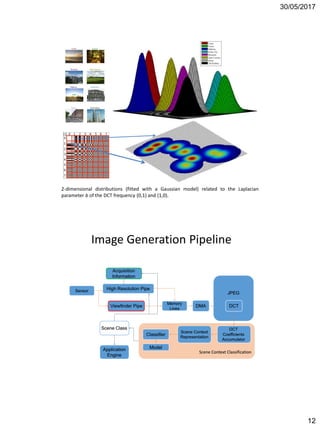
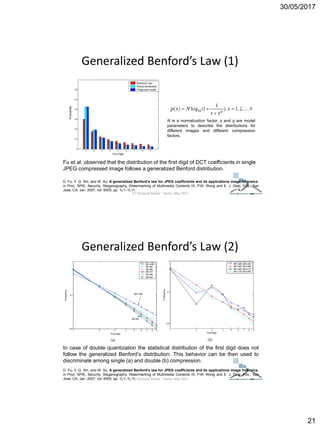
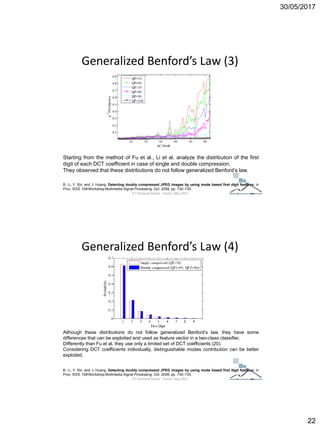
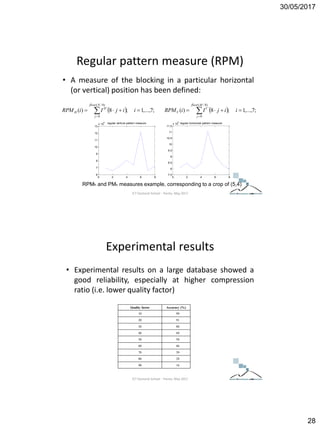
The document discusses techniques for detecting image forgeries by analyzing JPEG artifacts. It describes the JPEG compression process and how discrete cosine transform (DCT) is applied to blocks of pixels. Quantization tables are used to quantize DCT coefficients, with standard tables published by the Independent JPEG Group. Detection of image splicing involves analyzing DCT coefficient distributions to detect double JPEG compression. The document outlines categories for quantization step estimation and double quantization detection methods based on coefficient distributions, Benford's law, neural networks, and more.


![30/05/2017
6
Discrete Cosine Transform
• Next, each component (Y, Cb, Cr) of each 8×8 block is
converted to a frequency-domain representation, using a
normalized, two-dimensional type-II discrete cosine
transform (DCT).
• As an example, one such 8×8
8-bit subimage might be:
• Before computing the DCT of the subimage, its gray values are
shifted from a positive range to one centered around zero.
• For an 8-bit image each pixel has 256 possible values: [0,255].
To center around zero it is necessary to subtract by half the
number of possible values, or 128.
ICT Doctoral School - Trento, May 2017
Discrete Cosine Transform
The DCT transforms 64 pixels to
a linear combination of these 64
squares. Horizontally is u and
vertically is v.
• Subtracting 128 from each pixel value
yields pixel values on [ -128,127] and we
obtain the following matrix.
• The next step is to take the two-
dimensional DCT, which is given by:
where
is the horizontal spatial frequency, for the integers .
is the vertical spatial frequency, for the integers .
is a normalizing function
is the pixel value at coordinates
is the DCT coefficient at coordinatesICT Doctoral School - Trento, May 2017](https://image.slidesharecdn.com/multimediasecurity-doublequantization-170601090045/85/Multimedia-Security-JPEG-Artifact-details-6-320.jpg)

![30/05/2017
8
DCT example
ICT Doctoral School - Trento, May 2017
DCT Coefficients Quantization
• The DCT coefficients are quantized to a limited
number of possible levels.
• The Quantization is needed to reduce the
number of bits per sample.
Formula:
F( u, v) = round[ F( u, v) / Q( u, v)]
– Q( u, v) = constant => Uniform
Quantization.
– Q( u, v) = variable => Non-uniform
Quantization.
Example:
101000 = 40 (6 bits precision)
Truncates to 4 bits = 1000 = 8 (4 bits
precision).
i.e. 40/5 = 8, there is a constant N=5,
or the quantization or quality factor .
ICT Doctoral School - Trento, May 2017](https://image.slidesharecdn.com/multimediasecurity-doublequantization-170601090045/85/Multimedia-Security-JPEG-Artifact-details-8-320.jpg)
![30/05/2017
9
ICT Doctoral School - Trento,
May 2017
Quantization step
It is possible to approximate the statistical
distribution of the AC DCT coefficients, both
luminance and chrominance components, of a
8x8 block, by a Laplacian distribution in the
following way:
pi(x)= i /2 e-i |x| i = 1, 2, ..., 64;
where:
i= sqrt(2)/i ;
i = i-th DCT standard deviation;
EXAMPLE:
Q(u,v)= 8; Quantization Step
Round(256/8)= 32 Intervals;
[0, 8, 16, 24, 32, 40, ..., 256] - Reconstruction
Levels
Dead
zone
ICT Doctoral School - Trento, May 2017
Edmund Y. Lam, , Joseph W. Goodman - A Mathematical Analysis of the
DCT Coefficient Distributions for Images– IEEE Trans. On Image
Processing, Vol.9, No. 10, 2000](https://image.slidesharecdn.com/multimediasecurity-doublequantization-170601090045/85/Multimedia-Security-JPEG-Artifact-details-9-320.jpg)


















![30/05/2017
32
Farid, H.: Exposing digital forgeries from JPEG ghosts. IEEE Transactions on Information Forensics and Security 4(1),
154–160 (2009)
State of the art - Farid (2009)
ICT Doctoral School - Trento, May 2017
The Approach:
• quantize again such value with a novel quantization coefficient (q3)
varying in a proper range;
• evaluate an error function defined as follows:
Farid, H.: Exposing digital forgeries from JPEG ghosts. IEEE Transactions on Information Forensics and Security 4(1),
154–160 (2009)
• c is the DCT term;
• qi is the quantization coefficient referred to the i-th compression,
• […] indicates the round function
• |..| indicates the abs function
State of the art - Farid (2009)
ICT Doctoral School - Trento, May 2017](https://image.slidesharecdn.com/multimediasecurity-doublequantization-170601090045/85/Multimedia-Security-JPEG-Artifact-details-32-320.jpg)


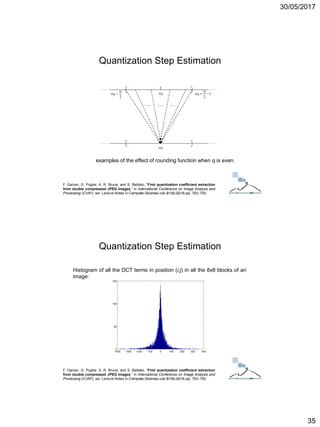
![30/05/2017
37
but: 𝑞2 < 𝑞1 → 𝑚𝑞2 (result is mapped in generic multiple of 𝑞2) where:
• 𝑐2 𝜖 [n𝑞2 − ⌊𝑞2/2⌋ ,n𝑞2+⌊𝑞2/2⌋] if 𝑞2 is odd;
• 𝑐2 𝜖 𝑛𝑞2 −
𝑞2
2
, 𝑛𝑞2 +
𝑞2
2
− 1 if 𝑞2 is even.
then in the range related to 𝑛𝑞1
F. Galvan, G. Puglisi, A. R. Bruna, and S. Battiato, “First quantization coefficient extraction
from double compressed JPEG images,” in International Conference on Image Analysis and
Processing (ICIAP), ser. Lecture Notes in Computer Science, vol. 8156, 2013, pp. 783–792.
Quantization Step Estimation
ICT Doctoral School - Trento, May 2017
if we quantize again with q1, we turn back to the situation
before the second quantization
F. Galvan, G. Puglisi, A. R. Bruna, and S. Battiato, “First quantization coefficient extraction
from double compressed JPEG images,” in International Conference on Image Analysis and
Processing (ICIAP), ser. Lecture Notes in Computer Science, vol. 8156, 2013, pp. 783–792.
Quantization Step Estimation
ICT Doctoral School - Trento, May 2017](https://image.slidesharecdn.com/multimediasecurity-doublequantization-170601090045/85/Multimedia-Security-JPEG-Artifact-details-37-320.jpg)


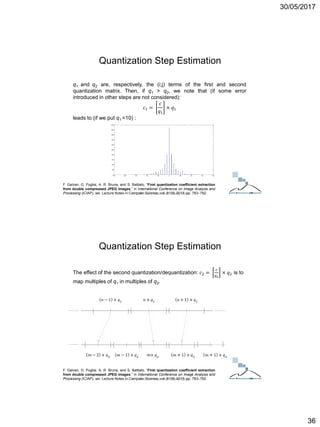
![30/05/2017
40
Summarizing:
a fourth quantization
with q2 will bring us at
the same situation
that we had after the
second quantization
F. Galvan, G. Puglisi, A. R. Bruna, and S. Battiato, “First quantization coefficient extraction
from double compressed JPEG images,” in International Conference on Image Analysis and
Processing (ICIAP), ser. Lecture Notes in Computer Science, vol. 8156, 2013, pp. 783–792.
Quantization Step Estimation
ICT Doctoral School - Trento, May 2017
The proposed error function (q3 is varying in a proper range) is:
If q3 = q1 the error function will be =0
F. Galvan, G. Puglisi, A. R. Bruna, and S. Battiato, “First quantization coefficient extraction
from double compressed JPEG images,” in International Conference on Image Analysis and
Processing (ICIAP), ser. Lecture Notes in Computer Science, vol. 8156, 2013, pp. 783–792.
• c is the DCT term;
• qi is the quantization coefficient referred to
the i-th compression,
• […] indicates the round function
• |..| indicates the abs function
Quantization Step Estimation
ICT Doctoral School - Trento, May 2017](https://image.slidesharecdn.com/multimediasecurity-doublequantization-170601090045/85/Multimedia-Security-JPEG-Artifact-details-40-320.jpg)