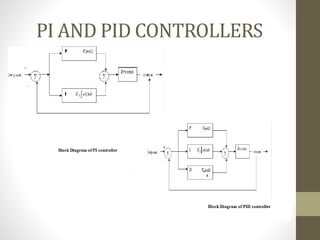
This document discusses using PI and PID controllers to control the vibration of a bus suspension system. It presents a quarter-bus model to simplify the suspension system to a single mass-spring-damper system. The open-loop response shows oscillations with a large settling time. To address this, closed-loop control with PI and PID controllers is proposed. The controllers use proportional, integral and derivative terms to increase response speed and eliminate steady state error from disturbances. Simulation results in MATLAB/Simulink will analyze and improve the bus suspension system response.

1. Control of vehicle
Suspension System using
PI and PID Controller
BY
VENKATA SIRISH KUMAR.A
NITHYA SANNAREDDY

2. INTRODUCTION
• The aim of the advanced bus suspension system is to provide
smooth ride and maintain the control of the vehicle over
cracks, uneven pavement of the road. Moreover, suspension
system modeling has an important role for realistic control
design of suspension
• PI and PID controllers are designed to control the vibration
occurred in bus suspension system using SIMULINK/MATLAB

3. PI AND PID CONTROLLERS

4. SUSPENSION SYSTEM
• Suspension system serves a dual purpose- contributing to the
vehicle's road holding/handling and braking for safety purpose and
pleasure driving, and keeping vehicle occupants comfortable and
isolated from road noise, bumps, and vibrations, etc.

5. PROBLEM FORMULATION
• When the suspension system is designed, a ¼ model of bus is
used to simplify the problem to a one dimensional mass-spring-
damper system. Its open-loop performance on the basis of time
response is observed which depicts that the bus suspension has
oscillations with large settling time. To overcome this problem,
closed-loop system is used.

6. BASIC EQUATIONS
• The dynamic equation by using the Newton’s law.
• Equations of Motion of quarter-bus model, given in equations (1) and (2) has been
transformed in state-space model, shown in equations (3) and (4) including
variable vector, disturbance vector and the input vector by applying some
algebraic operations on them.

7. CONTROL APPROACH
• The combination of proportional and integral terms is important to
increase the speed of the response and also to eliminate the steady
state error.
• The PID controller calculation involves three separate parameters,
and is accordingly sometimes called three-term control: the
proportional, the integral and derivative values, denoted P, I, and D.
The proportional value determines the reaction to the current error,
the integral value determines the reaction based on the sum of
recent errors, and the derivative value determines the reaction
based on the rate at which the error has been changing.
• The weighted sum of these three actions is used to adjust the
process via a control element such as the disturbances of a bus
suspension system.

8. PROPOSAL PROJECT PLAN
• Finding Response of Bus suspension system using PI & PID
controllers.
• Preparing the SIMULINK and MATLAB .
• Final result and conclusion .
• Preparing for final presentation.
• Bus suspension system is successfully implemented.

9. CONCLUSION
• The overshoot of open loop response and settling time can be
calculated which indeed signifies that people sitting in the bus
feel small amount of oscillation for unacceptably long time.
• The proposed model is intended to create and convey the
reaction of framework utilizing PID controller up to a superior
level.