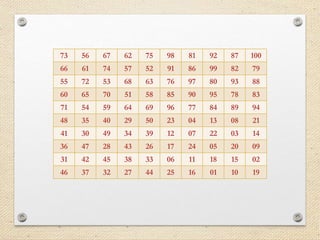
This document presents a summary of a project on solving the knight's tour problem. It discusses the knight's tour problem, concepts related to open and closed tours, and approaches to solving it through backtracking for small boards and divide-and-conquer for larger boards. It provides sample outputs for boards of sizes 5x5, 6x6, and 10x10, and discusses challenges faced and future work in solving the problem for general m x n boards.

1. Knight’s Tour
Presented by
Madhura Kaple
Ketki Kulkarni

2. Content
1. Problem Statement
2. Concepts
3. Implementation Approach
4. Demo
5. Output
6. Future Scope
7. Conclusion
8. Bibliography

3. Introduction
• A knight’s tour is a series of moves that knight makes
while visiting every cell of n x n of the chessboard
exactly once.
• Consider the n x n chessboard as a knight’s graph G
= (V, E) where vertices Є V represent the cell of the
chessboard and every edge Є E represent a knight’s
move from one cell to another.
• It is a special case of Hamiltonian-Path problem.

4. Related Concepts
• The knight tour can either be open or close.
• A knight’s tour is closed tour if a knight starts from
one cell and visits all other cells of n x n chessboard
exactly once and start position is reachable by one
knight’s move from last visited cell. Otherwise it is an
open path.
• A knight’s close tour is defined to be a Hamiltonian
cycle on a knight’s graph and a open path is defined
to be a Hamiltonian path.

5. Related Concepts Continued…
i j
I + 1 J + 2
I + 2 J + 1
I – 1 J + 2
I – 2 J + 1
I – 2 J - 1
I – 1 J - 2
I + 1 J - 2
I + 2 J - 1

6. Implementation Approach
• Used two approaches in solving this problem:
1. Finding the solution for base cases using the backtracking
technique.
2. Use of divide-and-conquer approach for the chessboards
with n ≥ 10.
• Distinguished between open path and closed tour
once tour was computed.

7. Building base cases
• Considered base cases as n = 5, 6, 7 and 8.
• Recursively checked if any further move(s) exist from
current cell. If exist then add current cell to the tour if
not then backtrack to previous cell’s possible moves.
• If exist then select its move as a current cell and again
recursively find possible moves.
• Continued till either a tour or path is obtained or there are
no further moves.

8. Divide-and-conquer approach
• For n x n chessboards with n ≥ 10, use divide and
conquer approach.
• Divide chessboard into four equal quadrants of size
n/2 x n/2.
• Find a tour for first quadrant and consider it as a
base case while finding the solution.
• Repeat this for each quadrant.

9. Divide-and-conquer approach
continued….
• Once tours for each quadrant is computed, combine
those tours to find a final tour.
• To combine tours take last vertex of each tour in
each quadrant and check if it can form a Knight's
tour to the starting vertex of the corresponding tour.
• Decide whether the tour is close tour or open path
based on a Hamiltonian problem.

10. Output
• For chessboard with n = 5 and starting point as (4, 0)
• This is an open path.
25 12 23 18 05
22 17 06 13 08
11 24 09 04 19
16 21 02 07 14
01 10 15 20 03

11. Output
• For chessboard with n = 6 and starting cell as (0, 0)
• This is an close cycle
07 26 01 18 05 24
36 17 06 25 34 19
27 08 35 02 23 04
16 11 14 31 20 33
13 28 09 22 03 30
10 15 12 29 32 21

12. Output
• For chessboard with n = 10 and starting point as (9,
7)
• This is an open path

13. 73 56 67 62 75 98 81 92 87 100
66 61 74 57 52 91 86 99 82 79
55 72 53 68 63 76 97 80 93 88
60 65 70 51 58 85 90 95 78 83
71 54 59 64 69 96 77 84 89 94
48 35 40 29 50 23 04 13 08 21
41 30 49 34 39 12 07 22 03 14
36 47 28 43 26 17 24 05 20 09
31 42 45 38 33 06 11 18 15 02
46 37 32 27 44 25 16 01 10 19

14. Challenges faced
• Selecting the base cases.
• Deciding the approach to merge four quadrants in
divide and conquer technique.

15. Future Scope
• As of now we have implemented knight’s tour for
the chessboard of size n x n with base cases n = 5, 6,
7 and 8.
• We plan to find a solution for m x n size chessboard .

16. Conclusion
• No open path or close cycle for chessboard with n
=3, 4.
• For all values of n ≥ 10, divide-and-conquer
approach takes less amount of time than that of
using backtracking.
• For n = 5, only open paths are found.
• For n = 6, 7 and 8, found both open paths and close
tours.

17. Bibliography
• https://larc.unt.edu/ian/pubs/algoknight.pdf
• http://www.sciencedirect.com/science/article/pii/S0166218X0400
3488
• http://www.sciencedirect.com/science/article/pii/S0166218X0400
3488
• https://en.wikipedia.org/wiki/Knight's_tour
• https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=we
b&cd=5&cad=rja&uact=8&ved=0ahUKEwjK5PLoz8DLAhVG8
GMKHWaCC5YQFgg7MAQ&url=https%3A%2F%2Fwww.cs.cm
u.edu%2F~sganzfri%2FKnights_REU04.pdf&usg=AFQjCNEzp1
2ah2hcM_1Ei73Mg_kzwLBHmQ&sig2=M9IK7h84lZ2kSUi5c8BP
Cw

18. Any Questions???

19. Thank you