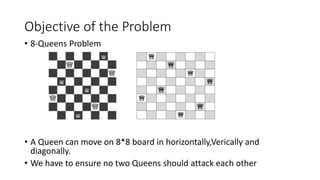
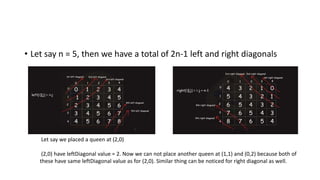
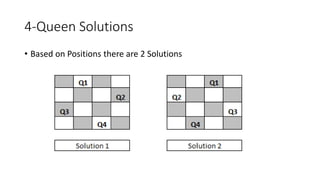
The document discusses the 8-Queens problem, which aims to place 8 queens on an 8x8 chessboard so that no two queens attack each other. It outlines the objective and constraints of ensuring no two queens are in the same row, column, or diagonal. Possible solutions are presented, along with a backtracking algorithm to systematically place queens one by one until a solution is found or no options remain.

1. 8-Queens Problem

2. Overview
• Objective of the Problem
• Constraints
• Solutions
• Conclusion

3. Objective of the Problem
• 8-Queens Problem
• A Queen can move on 8*8 board in horizontally,Verically and
diagonally.
• We have to ensure no two Queens should attack each other

4. Constraints
• Each row should contain single Queen
• Each column should contain single Queen
• If R-C=0 , then the Queens are under attack diagonally
• Based on the solutions, we can extract various constraints for
diagonal move of the Queen
• Row + Col = constant
• Row-Col + n-1 = constant

5. • Let say n = 5, then we have a total of 2n-1 left and right diagonals
Let say we placed a queen at (2,0)
(2,0) have leftDiagonal value = 2. Now we can not place another queen at (1,1) and (0,2) because both of
these have same leftDiagonal value as for (2,0). Similar thing can be noticed for right diagonal as well.

6. Concept to solve 8-Queens
• Decomposition
-Divide-and-Conquer
• Pattern Matching
- 4 Queens Solution
• Abstraction
- N Queens

7. 4-Queen Solutions
• Based on Positions there are 2 Solutions

8. 8-Queens Problem
• 3 Possible solutions
(1,5,2,6,3,7,4,8) (6,4,7,1,8,2,5,3)
(3,6,4,2,8,5,7,1)

9. Backtracking Solution - Algorithm
1) Start in the leftmost column
2) If all queens are placed
return true
3) Try all rows in the current column.
Do following for every tried row.
a) If the queen can be placed safely in this row
then mark this [row, column] as part of the
solution and recursively check if placing
queen here leads to a solution.
b) If placing the queen in [row, column] leads to
a solution then return true.
c) If placing queen doesn't lead to a solution then
unmark this [row, column] (Backtrack) and go to
step (a) to try other rows.
4) If all rows have been tried and nothing worked,
return false to trigger backtracking.

10. Conclusion
• We explain to students with use of Backtracking on 4-Queens
• For optimal Solution (for placement training), Dynamic Programming
mechanism can be utilized.

11. Suggestions?
Queries?