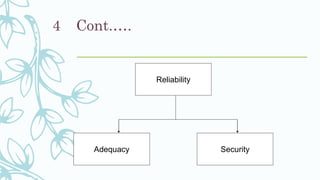
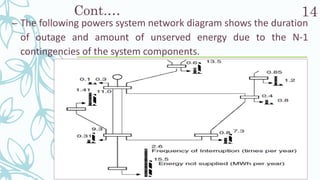
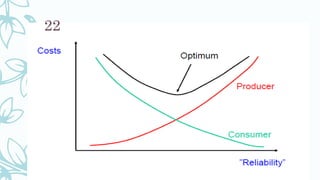
Chapter three of the document discusses power system reliability analysis, focusing on the concepts of reliability, adequacy, and security within power systems. It explains the need for sufficient facilities to meet consumer demand, evaluates transmission and distribution system reliability, and introduces various reliability indices to measure performance. Additionally, the chapter highlights the importance of understanding outage frequency, duration, and their economic impacts on service delivery.

1. POWER SYSTEM
PLANING AND
OPERATION
(PCE5312)
CHAPTER THREE: POWER
SYSTEM RELIABILITY ANALYSIS
BY: MESFIN M.

2. Outline
➢Introduction to Power System Reliability
➢Transmission network Reliability Analysis
➢Distribution System Reliability Analysis
➢Index of Reliability
2

3. Introduction
– Reliability generally describes the continuity of
electric service to customers
– Reliability primarily relates to equipment outages
and customer interruptions
– Actual service reliability can be quantified in terms :
outage frequency and outage duration.
– The product of outage frequency and average
duration gives the total outage time.
3

4. Cont.….
Reliability
SecurityAdequacy
4

5. Cont.…
– Adequacy relates to the existence of sufficient facilities within the
system to satisfy the consumer load demand
❑Three conditions must be met to ensure system adequacy:
I. Its available generation capacity must be greater than the
demanded load plus system losses.
II. It must be able to transport this power to its customers
without overloading any equipment.
III.It must serve its loads within acceptable voltage levels.
5

6. Cont.…
– System Security - the ability of a power system to
supply all of its loads in the event of one or more
contingencies.
– A measure of power system ability to withstand
sudden disturbances such as electric short circuits or
unanticipated losses of system components or load
conditions together with operating constraints.
6

7. Cont.…
– The simplest way in which utilities have traditionally
described their system’s reliability is in terms of:
– Reserve margin of generation resource:
– Loss-of-load probability (LOLP):
– Loss-of-load expectation (LOLE),
7

8. Cont.…
– Reserve margin of generation resource: that is excess
of the highest anticipated load. Before the
economic pressures that began to appear a reserve
margins of 20% were standard.
– Loss-of-load probability (LOLP): States the probability
that during any given time interval, the system wide
generation resources will fall short of demand.
8

9. Cont.…
– Loss-of-load expectation (LOLE): in which the
probability of loss-of-load for each day is summed
up over a time period and expressed as an inverse,
to state that we should expect one loss-of-load
event during this period.
9

10. Cont.…
– When comparing various power system design
alternatives there are two factors to be
considered:
1. Acceptable system performance quality factors
(including reliability) and
2. Cost are essential in selecting an optimum
design.
10

11. Transmission network Reliability
Analysis
– Transmission systems must meet performance
standards and criteria that ensure an acceptable
level of quality of electric service.
– Frequency is typically not an issue in large
interconnected systems with adequate generation
reserves. Similarly, voltage quality at the consumer
connection is typically addressed at the distribution
level and not by reinforcing the transmission
system.
11

12. Cont.…
– Additional transmission facilities will virtually
always increase reliability, but this remedy is
constrained by the cost of new facilities and
environmental impacts of new construction.
– Reliability objectives, therefore, must be defined
explicitly or implicitly in terms of the value of
reliable power supply to the consumer and to
society at large.
12

13. Probabilistic Transmission System
Analysis
– System reliability assessment and evaluation methods
based on probability theory allow the reliability of a
proposed system to be assessed quantitatively.
– Load interruption frequency and the expected duration
of load interruption events can be converted to an
average downtime per year.
– This can be converted to a cost by knowing the cost of
downtime for the facility.
13

14. Cont.…
– The following powers system network diagram shows the duration
of outage and amount of unserved energy due to the N-1
contingencies of the system components.
14

15. Cont.…
– Reliability can be measured by the frequency of
events having unacceptable impacts on the system
or on the consumer, and by the severity and
duration of the unacceptable impacts.
– There are three fundamental components of
reliability measures:
– Frequency of unacceptable events,
– Duration of unacceptable events, and
– Severity of unacceptable events.
15

16. Index of Reliability
– The index of reliability is a Convenient performance measure that
has been used in the past to provide an indication of positive
system performance.
𝐼𝑛𝑑𝑒𝑥 𝑜𝑓 𝑟𝑒𝑙𝑖𝑎𝑏𝑖𝑙𝑖𝑡𝑦 =
𝑡𝑜𝑡𝑎𝑙 𝑐𝑢𝑠𝑡𝑜𝑚𝑒𝑟 ℎ𝑟𝑠. 𝑝𝑒𝑟 𝑦𝑒𝑎𝑟 − (𝑡𝑜𝑡𝑎𝑙 𝑐𝑢𝑠𝑡𝑒𝑚𝑒𝑟 ℎ𝑟𝑠. 𝑖𝑛𝑡𝑟𝑟𝑢𝑝𝑡𝑒𝑑 𝑝𝑒𝑟 𝑦𝑒𝑎𝑟)
(𝑡𝑜𝑡𝑎𝑙 𝑐𝑢𝑠𝑡𝑒𝑚𝑒𝑟 ℎ𝑟𝑠. 𝑝𝑒𝑟 𝑦𝑒𝑎𝑟)
16

17. Cont.…
– Power system reliability analyses provide answers to the
following three issues:
– The level of reliability appropriate to serve adequately the
needs of customer.
– The various methods that could be used in order to
achieve such level of reliability and cost effectiveness
– The various procedure that might be used in the case of
emergency outage to minimize the public disruption and
economic loss.
17

18. The basic reliability concept:
– The probability of failure of a given component
(system) can be expressed as a function of time as:
𝑃(𝑇 <= 𝑡) = 𝐹(𝑡), 𝑡 >= 0
– Where T = random variable representing failure time
– F(t) = probability that component will fail by time , t
– The failure distribution function 𝐹(𝑡) is also defined
as the unreliability functions.
18

19. Cont.…
– The reliability function can be expressed as:
𝑅(𝑡) = 1 − 𝐹(𝑡) = 𝑃(𝑇 > 𝑡)
– Hence , the probability that the component will survive
at time t is defined as the reliability function 𝑅(𝑡).
𝑅 𝑡 = 1 − 𝐹(𝑡) = 1 − න
0
𝑡
𝑓 𝑡 𝑑𝑡 = න
1
∞
𝑓 𝑡 𝑑𝑡
𝑊ℎ𝑒𝑟𝑒
𝐹(𝑡) = න
0
𝑡
𝑓 𝑡 𝑑𝑡
19

20. Cont.…
– Provided that the time to failure, random variable 𝑇,
has a density function 𝑓(𝑡).
– Therefore, it is possible to express the probability of
failure of a given system in specific time interval
(𝑡1, 𝑡2) in terms of either the unreliability function.
20

21. Cont.…
න
𝑡1
𝑡2
𝑓 𝑡 𝑑𝑡 = න
−∞
𝑡2
𝑓 𝑡 𝑑𝑡 − න
−∞
𝑡1
𝑓 𝑡 𝑑𝑡 = 𝐹(𝑇2) − 𝐹(𝑇1)
– Or in terms of reliability function as:
න
𝑡1
𝑡2
𝑓 𝑡 𝑑𝑡 = න
𝑡1
∞
𝑓 𝑡 𝑑𝑡 − න
𝑡2
∞
𝑓 𝑡 𝑑𝑡 = 𝑅(𝑡1) − 𝑅(𝑡2)
21

22. 22

23. Distribution System Reliability
– Reliability problem increases as we go from generation
to distribution.
– The majority of customer reliability problems arise
from distribution systems.
– For a typical residential customer with 90 min of
interrupted power per year, between 70 and 80
minutes will be attributable to problems occurring on
the distribution system that it is connected to.
23

24. Cont.…
– In distribution systems, reliability primarily relates to
equipment outages and customer interruptions:
– Outage-when a piece of equipment is deenergized.
– Momentary interruption-when a customer is
deenergized for less than a few minutes.
– Sustained interruption-when a customer is deenergized
for more than a few minutes.
24

25. Cont.…
– Utilities typically keep track of customer reliability by
using reliability index. These are average customer
reliability values for a specific area.
– This area can be the utility’s entire service area, a
particular geographic region, a substation service
area, a feeder service area, and so on.
– The most commonly used reliability indices give each
customer equal weight.
25

26. Cont.…
– In order to quantify the effects of long interruption, interruption
indices are defined as Interruption Frequency, Supply
Unavailability and Interruption Duration.
– Interruption frequency represents the number of interruptions on
average per year per customer.
– Supply unavailability describes the number of minutes without
supply on average per year per customer, and Interruption
duration is the average duration of customer interruptions.
26

27. The most common of these customer
reliability indices are:
– System Average Interruption Frequency Index (SAIFI):It
is the average number of interruptions of supply in the
year for the customers who experience interruption of
supply.
𝑆𝐴𝐼𝐹𝐼 =
𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑐𝑢𝑠𝑡𝑜𝑚𝑒𝑟 𝑖𝑛𝑡𝑒𝑟𝑟𝑢𝑝𝑡𝑖𝑜𝑛
𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑐𝑢𝑠𝑡𝑜𝑚𝑒𝑟 𝑠𝑒𝑟𝑣𝑒𝑑
𝑆𝐴𝐼𝐹𝐼 =
σ 𝜆𝑖 𝑁𝑖
σ 𝑁𝑖
, 𝜆𝑖 𝑖𝑠 𝑓𝑎𝑖𝑙𝑢𝑟𝑒 𝑟𝑎𝑡𝑒
27

28. Cont.…
– System Average Interruption Duration Index (SAIDI):It is
the average total duration of interruptions of supply per
annum that a customer experiences.
𝑆𝐴𝐼𝐷𝐼 =
𝑆𝑢𝑚 𝑜𝑓 𝑐𝑢𝑠𝑡𝑜𝑚𝑒𝑟 𝑖𝑛𝑡𝑒𝑟𝑟𝑢𝑝𝑡𝑖𝑜𝑛 𝑑𝑢𝑟𝑎𝑡𝑖𝑜𝑛
𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑐𝑢𝑠𝑡𝑜𝑚𝑒𝑟 𝑠𝑒𝑟𝑣𝑒𝑑
𝑆𝐴𝐼𝐷𝐼 =
σ 𝑈𝑖 𝑁𝑖
σ 𝑁𝑖
Where 𝑈𝑖 𝑖𝑠 𝑎𝑛𝑛𝑢𝑎𝑙 𝑜𝑢𝑡𝑎𝑔𝑒 𝑡𝑖𝑚𝑒
28

29. Cont.…
– Customer Average Interruption Duration Index (CAIDI): It
is the average duration of an interruption of supply in
the year for customers who experience interruption
of supply.
𝐶𝐴𝐼𝐷𝐼 =
𝑆𝑢𝑚 𝑜𝑓 𝑐𝑢𝑠𝑡𝑜𝑚𝑒𝑟 𝑖𝑛𝑡𝑒𝑟𝑟𝑢𝑝𝑡𝑖𝑜𝑛 𝑑𝑢𝑟𝑎𝑡𝑖𝑜𝑛
𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑐𝑢𝑠𝑡𝑜𝑚𝑒𝑟 𝑖𝑛𝑡𝑒𝑟𝑟𝑢𝑝𝑡𝑖𝑜𝑛
𝐶𝐴𝐼𝐷𝐼 =
𝑆𝐴𝐼𝐷𝐼
𝑆𝐴𝐼𝐹𝐼
29

30. Cont.…
– Customer Average Interruption Frequency Index (CAIFI):
It is the average frequency of an interruption of
supply in the year for customers who experience
interruption of supply.
𝐶𝐴𝐼𝐹𝐼 =
𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑐𝑢𝑠𝑡𝑜𝑚𝑒𝑟 𝑖𝑛𝑡𝑒𝑟𝑟𝑢𝑝𝑡𝑖𝑜𝑛
𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑐𝑢𝑠𝑡𝑜𝑚𝑒𝑟𝑠 𝑖𝑛𝑡𝑒𝑟𝑟𝑢𝑝𝑡𝑒𝑑
30

31. Cont.…
– Average System Availability Index (ASAI): This is the
ratio of the total number of customer hours that
service was available during a year to the total
customer hours demanded.
𝐴𝑆𝐴𝐼 =
𝐶𝑢𝑠𝑡𝑜𝑚𝑒𝑟 ℎ𝑜𝑢𝑟𝑠 𝑜𝑓 𝑎𝑣𝑎𝑖𝑙𝑎𝑏𝑙𝑒 𝑠𝑒𝑟𝑣𝑖𝑐𝑒
𝑐𝑢𝑠𝑡𝑜𝑚𝑒𝑟 ℎ𝑜𝑢𝑟 𝑑𝑒𝑚𝑎𝑛𝑑
∗ 100%
𝐴𝑆𝐴𝐼 =
σ 𝑁𝑖 ∗ 8760 − σ 𝑈𝑖 𝑁𝑖
σ 𝑁𝑖 ∗ 8760
∗ 100%
31

32. Cont.…
– Average System unavailability Index (ASUI): This is the
ratio of the total number of customer hours that
service was unavailable during a year to the total
customer hours demanded.
𝐴𝑆𝑈𝐼 = (100 − 𝐴𝑆𝐴𝐼)%
32

33. End of Chapter three
Next
Chapter Four
33