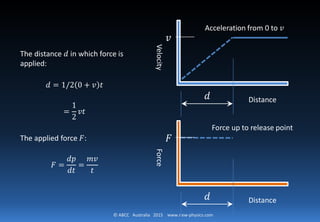
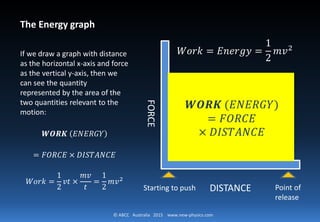
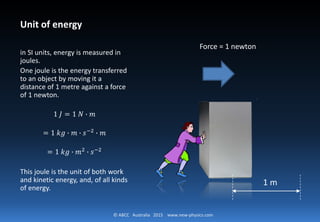
This document explains Newton's First Law of Motion, stating that a body at rest remains at rest and a body in motion continues in motion unless acted upon by an external force. It discusses the concepts of momentum, energy, and work in relation to force, defining energy in joules as the work done by a force moving an object over a distance. Additionally, it introduces the transfer of phonons as a representation of energy transfer during motion.

1. © ABCC Australia 2015 www.new-physics.com
ENERGY OF LINEAR MOTION

2. © ABCC Australia 2015 www.new-physics.com
Newton’s First Law of
Motion
Newton’s First Law of
Motion states that:
“A particle in rest will remain
forever at rest, and a particle in
uniform rectilinear motion will
continue to move on forever at
constant speed in the same
direction.
It will change its state of motion
only and only when it is
compelled to do so by forces
impressed on it.”
I

3. © ABCC Australia 2015 www.new-physics.com
First Law of Motion
According to Newton’s First Law
of Motion, a material body of
mass 𝑚𝑚𝑝𝑝 staying at rest will
remain at rest indefinitely.
Its velocity 𝑣𝑣 is zero:
𝑣𝑣 = 0
Subsequently, its momentum 𝑝𝑝𝑝𝑝
is zero:
𝑝𝑝𝑝𝑝 = 𝑚𝑚𝑝𝑝 𝑣𝑣 = 0 The statue is on a skateboard
to eliminate resistance from the ground

4. © ABCC Australia 2015 www.new-physics.com
Body in Motion
Also according to Newton’s First
Law of Motion, the particle or
material body in motion will
remain in motion indefinitely.
Its velocity 𝑣𝑣 is:
𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉 = 𝑣𝑣
Subsequently, its momentum 𝑝𝑝𝑝𝑝
becomes:
𝑝𝑝𝑝𝑝 = 𝑚𝑚𝑝𝑝 𝑣𝑣
Assuming that there is no air resistance to the
movement which will cause loss in momentum & energy

5. © ABCC Australia 2015 www.new-physics.com
Change in Dynamical States
𝑣𝑣𝑝𝑝 = 0
𝑝𝑝𝑝𝑝 = 0
𝑣𝑣𝑝𝑝
𝑝𝑝𝑝𝑝 = 𝑚𝑚𝑝𝑝 𝑣𝑣
There is an
obvious change in
the dynamic
states of the
system Change

6. © ABCC Australia 2015 www.new-physics.com
Force Effects the Change
According to the First Law, there must be an external force responsible for such a
change. In this case, it the push or pull exerted by an external agent – the mover.
𝑣𝑣𝑝𝑝 = 0 → 𝑣𝑣𝑝𝑝
𝑝𝑝𝑝𝑝 = 0 → 𝑚𝑚𝑝𝑝 𝑣𝑣
The mover exerts a
force 𝑭𝑭 on the statue
The statue moves
after the push
𝐹𝐹

7. © ABCC Australia 2015 www.new-physics.com
The distance 𝑑𝑑 in which force is
applied:
𝑑𝑑 = 1/2 0 + 𝑣𝑣 𝑡𝑡
=
1
2
𝑣𝑣𝑡𝑡
The applied force 𝐹𝐹:
𝐹𝐹 =
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
=
𝑚𝑚𝑚𝑚
𝑡𝑡
Acceleration from 0 to 𝑣𝑣
Velocity
Distance
𝑣𝑣
𝑑𝑑
Force
Distance
𝐹𝐹
𝑑𝑑
Force up to release point

8. © ABCC Australia 2015 www.new-physics.com
The Energy graph
If we draw a graph with distance
as the horizontal x-axis and force
as the vertical y-axis, then we
can see the quantity
represented by the area of the
two quantities relevant to the
motion:
𝑾𝑾𝑾𝑾𝑾𝑾𝑾𝑾 𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸
= 𝐹𝐹𝐹𝐹𝐹𝐹𝐹𝐹𝐹𝐹 × 𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷
𝑊𝑊𝑊𝑊𝑊𝑊𝑊𝑊 =
1
2
𝑣𝑣𝑣𝑣 ×
𝑚𝑚𝑚𝑚
𝑡𝑡
=
1
2
𝑚𝑚𝑣𝑣2
FORCE
DISTANCE
𝑾𝑾𝑾𝑾𝑾𝑾𝑾𝑾 (𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸)
= 𝐹𝐹𝐹𝐹𝐹𝐹𝐹𝐹𝐹𝐹
× 𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷𝐷
Starting to push Point of
release
𝑊𝑊𝑊𝑊𝑊𝑊𝑊𝑊 = 𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸 =
1
2
𝑚𝑚𝑣𝑣2

9. © ABCC Australia 2015 www.new-physics.com
Energy in terms of Work
So energy may have many forms.
But whatever form it may be,
the basic definition of energy is
expressed in terms of work:
Work
In physics, the definition is even
more precise. Work is done
when a force 𝐹𝐹 moves a body
through a distance 𝑑𝑑:
𝑊𝑊𝑊𝑊𝑊𝑊𝑊𝑊 = 𝐹𝐹 × 𝑑𝑑 d
F
Work = F x d

10. © ABCC Australia 2015 www.new-physics.com
Unit of energy
in SI units, energy is measured in
joules.
One joule is the energy transferred
to an object by moving it a
distance of 1 metre against a force
of 1 newton.
1 𝐽𝐽 = 1 𝑁𝑁 ∙ 𝑚𝑚
= 1 𝑘𝑘𝑘𝑘 ∙ 𝑚𝑚 ∙ 𝑠𝑠−2
∙ 𝑚𝑚
= 1 𝑘𝑘𝑘𝑘 ∙ 𝑚𝑚2
∙ 𝑠𝑠−2
This joule is the unit of both work
and kinetic energy, and, of all kinds
of energy.
1 m
Force = 1 newton

11. © ABCC Australia 2015 www.new-physics.com
Transfer of energy =
transfer of phonon
As we have established in our
previous discussions, the
application of force is equivalent
to the injection of phonons from
one object to another. Since
phonons are the carriers of
energy, they will be transferred
from one body to another
whenever a force is applied. If
the force is continuous over a
distance, the quantity of phonon
will build up until the force
stops. Then the energy of the
body is equal to the total
amount of phonons injected and
retained by the body..
Force MotionPhonons
transferred

12. © ABCC Australia 2015 www.new-physics.com
Energy-Phonon
Equivalence
The interpretation of energy by
phonons is therefore even
simpler.
Since energy is conserved:
1
2
𝑚𝑚𝛾𝛾 𝑐𝑐2
=
1
2
𝑚𝑚𝑝𝑝 𝑣𝑣2
Or:
𝑚𝑚𝛾𝛾 𝑐𝑐2
= 𝑚𝑚𝑝𝑝 𝑣𝑣2
We can see that the work done is
actually the transfer of phonons
from the mover to the moved.
The movedThe phononsThe mover

13. © ABCC Australia 2015 www.new-physics.com
TRANSFER TO OTHER ENERGY FORMS
To be continued on:
ABCC