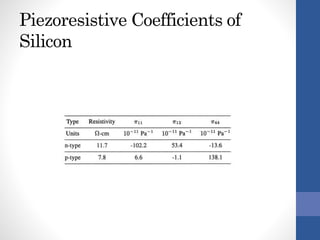
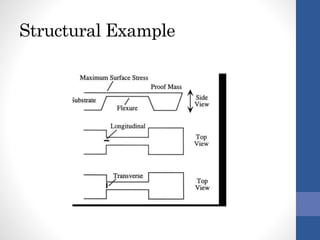
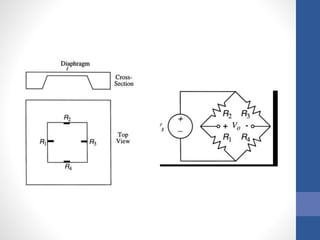
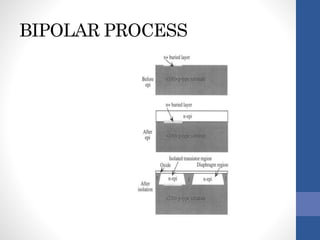
The document discusses a piezo resistive pressure sensor and the Motorola MAP sensor case study. It first explains pressure sensing methods and piezo resistivity. It then provides details on the Motorola MAP sensor, which uses a single piezo resistor on a silicon diaphragm and integrates signal conditioning. Finally, it analyzes stresses on the diaphragm and describes the sensor's signal conditioning and temperature compensation to reduce offset and improve sensitivity.

1. Piezo Resistive Pressure Sensor
&
Case Study of MAP Sensor
By
Pratyusha
And
A.Jenifer Sofia

2. Contents
Pressure Sensing
Piezo resistance
Case Study-Motorola MAP Sensor

3. Pressure Sensing
Pressure Sensing Methods:
By using piezoelectric material
By using piezo resistive material
Deformation Sensing Techniques:
 Position Measuring Techniques
To measure bending strain
By creating a resonant structure

4. Piezoresistivity
 Change in electrical resistivity when
mechanical stress is applied
Affects metals as well as semiconductors

5. Analytic Formulation in Cubic
Materials
 The relationship between electric field and
current density is given by 𝜀 = 𝜌ℯ + π. 𝜎 . 𝒥
Where
𝜌ℯ is the resistivity tensor of second rank
𝜋 is the fourth rank piezo resistive tensor
𝜎 is the full second-rank stress tensor, and
𝒥 is the current density.

6. Piezoresistive Coefficients of
Silicon

7. Structural Example

9. MOTOROLA MAP SENSOR
The Motorola manifold-absolute-pressure
(MAP) sensor uses piezo resistance to measure
diaphragm bending.
It integrates the signal-conditioning and
calibration circuitry onto the same chip as the
diaphragm.
PROCESS FLOW
 First, it is the only high-volume fully-integrated silicon pressure
sensor in the automotive market.
 Second, it uses bipolar transistors .
 Third, it uses only one piezo resistor.

10. BIPOLAR PROCESS

11. The transistors are built in an epitaxial n-silicon
layer that is grown on a (100) p-type substrate.
Transistors must be laterally isolated from one
another, by a deep p-type diffusion through the n-
epilayer, creating a p-n junction all the way
around the device prior to the growth of the
epitaxial layer, an n+ diffusion is placed beneath
each transistor region.
This buried layer helps provide low-resistance
connection to the collector of each transistor.
When the epitaxial layer is grown, this buried layer
diffuses part way into the epilayer, as shown in the
final diagram.

12. DETAILS OF DIAPHRAGM
AND PEIZORESISTOR
Diaphragm dimensions are 1000 × 1000 um
square, with a thickness of 20 um
Piezo resistor is located near the edge center,
where stress is highest, oriented at a 45 angle to the
side of the square diaphragm
The p-type piezo resistor has four contacts two-
current along the resistor axis and two - transverse
voltage taps which are connected to a impedance
op-amp input.
The other two are transverse voltage taps which
are connected to a high-impedance op-amp input
so as to draw no current

13. MOTOROLA XDUCER
PEIZORESISTOR

14. The dark-shaded contact regions are much
wider than the piezoresistor and are doped p+;
hence these regions have lower resistance than
the piezoresistor itself.
Diaphragm edge is along a [110] direction in a
(100) plane, it means that the resistor axis is
actually along a [100] direction.
We select an axis system in which the “1” axis
is along the resistor length, the “2” axis is in the
plane of the diaphragm, and the “3” axis is
normal to the diaphragm

15. The only non-zero current density is J1
However, the electric field in the transverse
direction is not zero.
We can see this from the piezoresistive
equations for the case J2 and J3=0 and =0 T
13=0 which would be the case for small
amplitude bending of the diaphragm under a
pressure load.

16. Assume J1 does not vary with depth, the voltage
along the length of the piezoresistor is given by
 where is LR the length of the piezoresistor and
x1 is the spatial coordinate for an axis aligned
along the resistor length.
Prefactor is the voltage due to the unstrained
resistivity of the piezoresistor.

17. The integral term is the change in voltage due
to a length averaging of the piezoresistance
effect
Part of the resistor is off the diaphragm, where
stress is low, and part of the resistor is away
from the edge of the diaphragm, it is
reasonable to assume that the average stresses
giving rise to axial piezoresistivity are
substantially less than the maximum stresses at
the diaphragm edge

18. STRESS ANALYSIS
An approximate model for the bending of a plate
under the effects of a pressure load is given by
The energy-method analysis with this trial
function led to a load-deflection equation of the
form
 For the present analysis,it is zero because the
diaphragm is bulk micromachined.

19. Neglecting , and from variation analysis
then, pressure defection is given as,
To calculate the shear stress
 Find the z-directed radius of curvature
Assuming that the piezoresistor depth is
small compared to the diaphragm
thickness
We resolve these two principal-axis stress
components into the shear stress in a
coordinate system rotated by 45°
sC 6
4

bC

20. SIGNAL-CONDITIONING AND
CALIBRATION
There is some offset at zero pressure.
Increasing temperature - offset increases & the
slope of the characteristics decreases
This indicates the reduction of piezo resistive
sensitivity with increasing temperature.
Since offset and sensitivity have opposite
temperature dependences, the curves all
intersect within a small region, referred to as
the “pivot point.”

21. TEMPERATURE
COMPENSATION OF SPAN

22. • The analysis is given as
TEMPERATURE COMPENSATION OF OFFSET
The device is then heated, and,
with minimum pressure applied, the offset is
once-again trimmed. The most recent devices
include an on-chip heater that supports this
calibration step.

23. DEVICE NOISE
System noise comes from several source
- noise in the piezo resistors
- front-end amplifier noise, presumed to
have both a white and 1/f component.
RECENT DESIGN CHANGES
Thus, an improvement in control of one
dimension allows a dramatic reduction in chip size,
from 3.05 mm square to 2.76 mm square, a 22%
area reduction.

24. HIGHER-ORDER EFFECTS
 The longitudinal piezoresistance,
 Detailed modeling of the stress distribution in
the diaphragm
 Nonlinearities in the temperature coefficient
of resistance
 Issues of resistor placement and stress
averaging