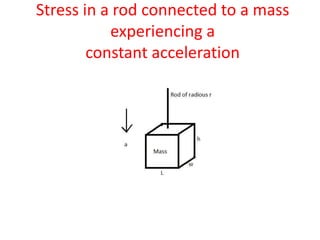
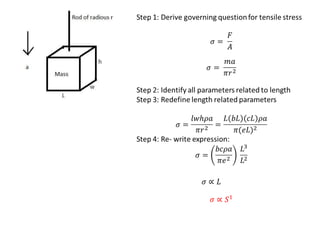
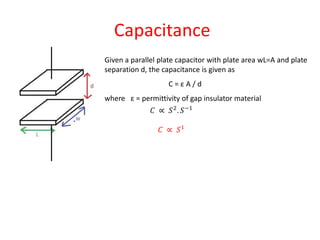
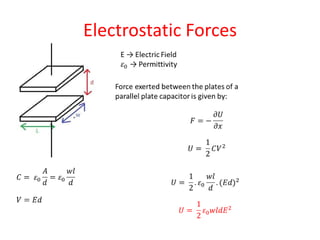
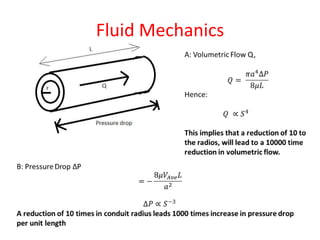
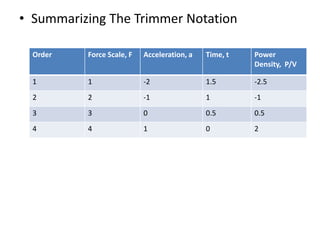
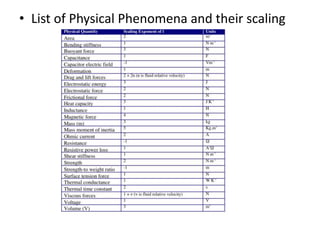
This document discusses scaling laws and how physical phenomena are affected as the size of systems decrease. Some key effects of decreasing size include friction and surface forces becoming more dominant over inertia and mass. Heat dissipation also increases relative to heat storage. Scaling laws can be used to determine how physical quantities vary with size, allowing evaluation of whether phenomena will scale favorably or poorly. The document provides several examples of how forces, resistance, capacitance and other factors are impacted by scaling and outlines approaches for systematically analyzing scaling effects using dimensional analysis and matrix formalization.

1. Scaling Laws

2. Micro Intuition
• Linear extrapolation is easy but we are at a loss
when considering the implications that shrinking
of length has on surface area to volume ratios
and on the relative strength of external forces
• Micro intuition can be misleading.
• Our aim is to develop a systematic approach
about the likely behavior of downsized systems
so we do not need to rely on micro intuition
alone.

3. Scaling Laws
• They allow us to determine whether physical
phenomena will scale more favorably or will
scale poorly.
• Generally, smaller things are less effected by
volume dependent phenomena such as mass
and inertia, and are more effected by surface
area dependent phenomena such as contact
forces or heat transfer.

4. As you decrease the size
• Friction > inertia
• Heat dissipation > Heat storage
• Electrostatic force > Magnetic Force

5. Surface Area to Volume Ratio

6. Surface Area : Volume Ratio
For Example

7. What are the implications of this?

8. • Volume relates, for example, to both
mechanical and thermal inertia. Thermal
inertia is a measure on how fast we can heat
or cool a solid. It is an important parameter in
the design of a thermally actuated devices.

9. Thermal Scaling
• Small object will loose heat rapidly, the
dissipation of waste heat is not problematic in
many cases.

10. Mathematical Approach
• Mathematically, a scaling law is a law that
describes the variations of physical quantities
with the size of the system.
• Use of dimensional analysis.

11. Scaling effects on spring constant (k)
• Consider a beam, length L, width w, Thickness
t, and Youngs Modulus E.

13. Stress in a rod connected to a mass
experiencing a
constant acceleration

15. Resistance

16. Resistance

17. Capacitance
Given a parallel plate capacitor with plate area wL=A and plate
separation d, the capacitance is given as
C = ε A / d
where ε = permittivity of gap insulator material

18. Electrostatic Forces

19. Electrostatic Forces

20. Electromagnetism
• Faraday’s law governs the induced force (or a motion)
in the wire under the influence of a magnetic field.
• The scaling of electromagnetic force follows: F ∝ S4.
• For electromagnets, as S decreases, these forces
decrease because it is difficult to generate large
magnetic fields with small coils of wire.
• However permanent magnets maintain their strength
as they are scaled down in size, and it is often
advantageous to design magnetic systems that use the
interaction between an electromagnet and a
permanent magnet.

21. Magnet Scaling

23. Fluid Mechanics

24. Use of Matrix Formalization
• To design micromechanical actuators, it is
helpful to understand how forces scale. Use of
a matrix formalism notation is very handy to
describe how different forces scale into the
small (and large) domain. It is called the
Trimmer’s vertical bracket approach.
• Formulated by William Trimmer in 1986.

25. Use of Matrix Formalization
• The top element in this notation refers to the case where
the force scales as S1. The next one down refers to a case
where the force scales as S2, etc.
• If the system becomes one-tenth its original size, all the
dimensions decrease by a tenth. The mass of a
system, m, scales as (S3) and, as systems become
smaller, the scaling of the force also determines the
acceleration (a), transit time (t), and the amount of power
per unit volume (PV-1)

26. Scaling of forces
• The force due to surface tension scales as S1
• The force due to electrostatics with constant
field scales as S2
• The force due to certain magnetic forces
scales as S3
• Gravitational forces scale as S4

30. • Summarizing The Trimmer Notation
Order Force Scale, F Acceleration, a Time, t Power
Density, P/V
1 1 -2 1.5 -2.5
2 2 -1 1 -1
3 3 0 0.5 0.5
4 4 1 0 2

31. • List of Physical Phenomena and their scaling

32. Benefits Of Scaling
• Speed (Frequency increase, Thermal Time
constraints reduce)
• Power Consumption (actuation energy
reduce, heating power reduces)
• Robustness (g-force resilience increases)
• Economy (batch fabrication)