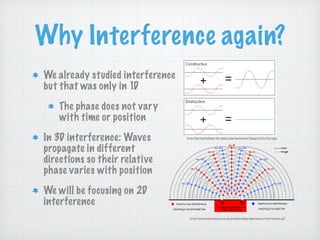
This document discusses two-dimensional interference patterns that arise when waves propagate in different directions. It explains that constructive interference occurs when the path difference between two waves is an integer multiple of the wavelength, causing the amplitudes to add. Destructive interference happens when the path difference is a half-integer multiple of the wavelength, reducing the amplitude. Formulas are provided for calculating the conditions of constructive and destructive interference between two waves.

1. Interference
Chapter 15-5
L02
http://i.ytimg.com/vi/fjaPGkOX-wo/maxresdefault.jpg

2. Why Interference again?
We already studied interference
but that was only in 1D
The phase does not vary
with time or position
In 3D interference: Waves
propagate in different
directions so their relative
phase varies with position
We will be focusing on 2D
interference
http://method-behind-the-music.com/mechanics/images/interfere.png
http://www.cyberphysics.co.uk/graphics/diagrams/waves/interference.gif

3. Constructive/
Destructive
Remember:
When two waves with same wavelength and
frequency are in phase, they are constructive.
The amplitudes add at these points
When two waves with same wavelength and
frequency are out of phase they are destructive
Amplitude usually decreases

4. Constructive
interference
Two points have to be in phase, regardless of
time
Constructive interference means that both
sources are at the peak positive amplitude (when
both sources are at the peak positive amplitude)
Then, there is an integer number of
wavelengths between each source and the
point under consideration

5. Constructive
interference
Any point that is an
integer multiple of
wavelength from
both sources will
undergo continuous
constructive
interference http://blog.ocad.ca/wordpress/gdes3b78-fw201203-01/files/2013/03/wave.jpg

6. The Math of Constructive
Interference
If d1 = path length from source 1 and d2 = path length from
source 2 the condition for constructive interference is :
d1 = mλ, m=1,2,3, …
d2 = nλ, n=1,2,3, …
The difference between the distances from the two
sources to the point of constructive interference is given
by:
Δd = d2 -d1 = (n-m)λ = pλ where p = 0, ±1, ±2, ±3, …

7. Condition for
Constructive Interference
Path difference
condition: The path
difference between
the two sources must
be an integer multiple
of the wavelength http://www.physicsclassroom.com/Class/light/u12l3b11.gif

8. BUT WAIT
What we just did
demands that both paths
individually be integer
multiples of wavelength.
But this does not have to
be true…
http://1.bp.blogspot.com/-QpnXjGcLfg0/Tw25JfjDQLI/AAAAAAAAAlo/QfGAyNhVR0w/s1600/huh.gif

9. The path difference
condition
Remember the path
difference condition?
That condition might
be sufficient enough to
produce constructive
interference
https://coherence.files.wordpress.com/2011/10/waves.png

10. Spherical waves
As spherical waves travel away from its source, it
oscillates in space and time
The amplitude is constant over any spherical
surface centred on the source
Spatial variations are described as a function
of r, the distance from the source. The wave
function becomes:
s(r,t) = sm(r)cos(kr-ωt+ )

11. The function
s(r,t) = sm(r)cos(kr-ωt+ ) may look familiar
to you
Recall: s(x,t) = sm(r)cos(kx-ωt+ )
The only difference is that our new
equation replaces x with r. This is
because the wave spreads out over a
larger area as it propagates outwards

12. The Math of Constructive
Interference, Again…
For two waves to be in phase, the arguments
of the cosine function must differ by an
integer multiple of 2∏.
Both waves are in phase so:
(kd2-ωt) - (kd1-ωt) = k(d2-d1) = n2∏
Therefore: (d2-d1) = n(2∏/k) = nλ , n = 0, ±1, ±2,
±3

13. Confusion?
Remember how in our initial condition
we got:
Δd = d2 -d1 = (n-m)λ = pλ where p = 0, ±1, ±2,
±3, …
But both paths individually had to be
integer multiples of wavelength.
We just demonstrated that this does not
always have to be the case since:
(d2-d1) = n(2∏/k) = nλ , n = 0, ±1, ±2, ±3 http://fc01.deviantart.net/fs70/f/2012/023/3/f/unagi_by_co__existance-d4ndy09.png

14. Constructive
Interference Formula
Constructive interference occurs
whenever the path difference is an
integer multiple of the wavelength.
In a special case where d2= d1= d, we
can add the two waves together to
find a resultant wave equation:
s(d,t) = 2sm(d)cos(kd-ωt+ )

15. Destructive Interference
Occurs when one path is an integer number of wavelengths
and the other is a half-integer multiple multiple
Therefore: The path difference is a half-integer multiple
of the wavelength (odd number of half wavelengths)
Equation: Δd = d2 -d1 = ((2n+1)/2)λ = (n+1/2)λ where n = 0,
±1, ±2, ±3
http://www.museevirtuel.ca/media/edu/EN/uploads/image/LO13DA3E7746049674775238736.jpg

16. Tips for 2-D Interference
The equations discussed may look complex. Try and
understand what each individual variable
represents
Remember, 2D interference is still interference so
if you get confused try and remember 1D
interference. It might help clarify certain
concepts for you.
Interference: Two or more waves combining to
produce a resultant wave